Bribery as a Measure of Candidate Success: Complexity Results for Approval-Based Multiwinner Rules
Paper and Code
Apr 19, 2021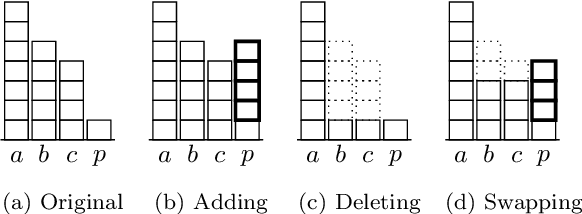
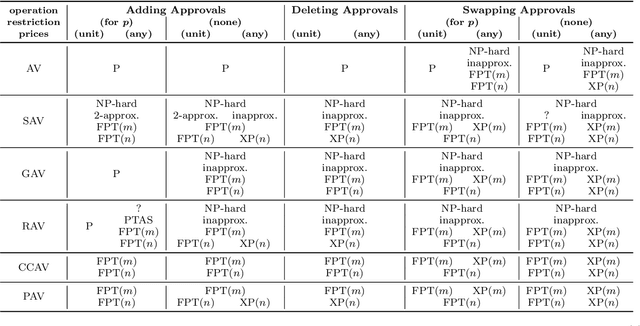
We study the problem of bribery in multiwinner elections, for the case where the voters cast approval ballots (i.e., sets of candidates they approve) and the bribery actions are limited to: adding an approval to a vote, deleting an approval from a vote, or moving an approval within a vote from one candidate to the other. We consider a number of approval-based multiwinner rules (AV, SAV, GAV, RAV, approval-based Chamberlin--Courant, and PAV). We find the landscape of complexity results quite rich, going from polynomial-time algorithms through NP-hardness with constant-factor approximations, to outright inapproximability. Moreover, in general, our problems tend to be easier when we limit out bribery actions on increasing the number of approvals of the candidate that we want to be in a winning committee (i.e., adding approvals only for this preferred candidate, or moving approvals only to him or her). We also study parameterized complexity of our problems, with a focus on parameterizations by the numbers of voters or candidates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge