Achieving Fully Proportional Representation: Approximability Results
Paper and Code
Dec 14, 2013


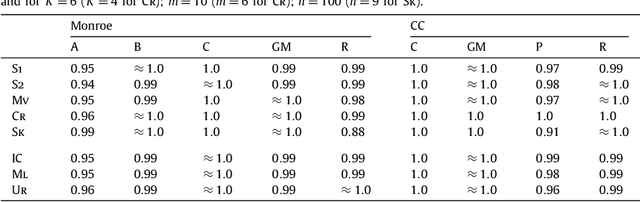
We study the complexity of (approximate) winner determination under the Monroe and Chamberlin--Courant multiwinner voting rules, which determine the set of representatives by optimizing the total (dis)satisfaction of the voters with their representatives. The total (dis)satisfaction is calculated either as the sum of individual (dis)satisfactions (the utilitarian case) or as the (dis)satisfaction of the worst off voter (the egalitarian case). We provide good approximation algorithms for the satisfaction-based utilitarian versions of the Monroe and Chamberlin--Courant rules, and inapproximability results for the dissatisfaction-based utilitarian versions of them and also for all egalitarian cases. Our algorithms are applicable and particularly appealing when voters submit truncated ballots. We provide experimental evaluation of the algorithms both on real-life preference-aggregation data and on synthetic data. These experiments show that our simple and fast algorithms can in many cases find near-perfect solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge