Generative Frontier Planning for Adaptive Peer-Referral Recruitment under Covariate-Dependent Arrivals

Peer-referral recruitment systems such as respondent-driven sampling are critical for studying and intervening on hidden populations affected by infectious diseases. To accelerate recruitment, public health agencies must adaptively allocate limited referral resources across multiple rounds, where current decisions shape both the number and the covariates of future recruits. Prior work makes this problem tractable by assuming that referrals are drawn i.i.d.\ from a homogeneous population, an assumption that ignores the homophily and shared context that drive real peer recruitment. We instead consider a more realistic model in which both referral capacity and the covariates of newly referred individuals are conditioned on the referrer, learned from data with a censored count model and a conditional generative model. The resulting planning problem is challenging because each candidate allocation induces a different distribution over future recruits. We propose \emph{Generative Frontier Planning} (GFP), a model-based planner that replaces per-step Monte-Carlo sampling with a deterministic backup over a latent covariate-coverage value surrogate. The surrogate is designed so that the expected value of the next frontier depends on the offspring generative model only through finite-dimensional summaries that are amortized offline, and so that the resulting per-round objective is monotone with diminishing returns. Together, these two properties make planning tractable: the deterministic backup eliminates Monte-Carlo sampling, and the diminishing-returns structure lets a marginal greedy allocation achieve a \((1-1/e)\)-approximation for the per-round problem. On a simulation environment calibrated to a real respondent-driven sampling dataset, GFP outperforms random, reinforcement-learning, and i.i.d.\ dynamic-programming baselines across four discount factors.

How LLMs Are Persuaded: A Few Attention Heads, Rerouted

Language models can be persuaded to abandon factual knowledge. This vulnerability is central to AI safety, but its internal mechanism remains poorly understood. We uncover a compact causal mechanism for persuasion-induced factual errors. A small set of mid-layer attention heads almost entirely determines the model's answer. These heads write answer options into a low-dimensional polyhedron, with options occupying distinct vertices. Persuasion does not blur belief or merely reduce confidence; it causes a discrete latent jump from the correct-answer vertex to the persuasion-target vertex. We show that decision heads are not reasoning over evidence. Instead, they copy whichever option token their attention selects. Persuasion works by redirecting attention. We isolate a rank-one evidence-routing feature that controls the route. Directly modifying this feature steers the model's choice, and removing it blocks persuasion. We then trace the feature back to a band of shallower attention heads that build it from persuasive keywords in the input. Every step is validated by intervention. This mechanism appears across open-source LLMs and realistic poisoning scenarios such as Generative Engine Optimization, revealing persuasion as a narrow, monitorable circuit.

Intern-S1-Pro: Scientific Multimodal Foundation Model at Trillion Scale

We introduce Intern-S1-Pro, the first one-trillion-parameter scientific multimodal foundation model. Scaling to this unprecedented size, the model delivers a comprehensive enhancement across both general and scientific domains. Beyond stronger reasoning and image-text understanding capabilities, its intelligence is augmented with advanced agent capabilities. Simultaneously, its scientific expertise has been vastly expanded to master over 100 specialized tasks across critical science fields, including chemistry, materials, life sciences, and earth sciences. Achieving this massive scale is made possible by the robust infrastructure support of XTuner and LMDeploy, which facilitates highly efficient Reinforcement Learning (RL) training at the 1-trillion parameter level while ensuring strict precision consistency between training and inference. By seamlessly integrating these advancements, Intern-S1-Pro further fortifies the fusion of general and specialized intelligence, working as a Specializable Generalist, demonstrating its position in the top tier of open-source models for general capabilities, while outperforming proprietary models in the depth of specialized scientific tasks.

Reward Shaping for Inference-Time Alignment: A Stackelberg Game Perspective

Existing alignment methods directly use the reward model learned from user preference data to optimize an LLM policy, subject to KL regularization with respect to the base policy. This practice is suboptimal for maximizing user's utility because the KL regularization may cause the LLM to inherit the bias in the base policy that conflicts with user preferences. While amplifying rewards for preferred outputs can mitigate this bias, it also increases the risk of reward hacking. This tradeoff motivates the problem of optimally designing reward models under KL regularization. We formalize this reward model optimization problem as a Stackelberg game, and show that a simple reward shaping scheme can effectively approximate the optimal reward model. We empirically evaluate our method in inference-time alignment settings and demonstrate that it integrates seamlessly into existing alignment methods with minimal overhead. Our method consistently improves average reward and achieves win-tie rates exceeding 66% against all baselines, averaged across evaluation settings.

Latent Spherical Flow Policy for Reinforcement Learning with Combinatorial Actions

Reinforcement learning (RL) with combinatorial action spaces remains challenging because feasible action sets are exponentially large and governed by complex feasibility constraints, making direct policy parameterization impractical. Existing approaches embed task-specific value functions into constrained optimization programs or learn deterministic structured policies, sacrificing generality and policy expressiveness. We propose a solver-induced \emph{latent spherical flow policy} that brings the expressiveness of modern generative policies to combinatorial RL while guaranteeing feasibility by design. Our method, LSFlow, learns a \emph{stochastic} policy in a compact continuous latent space via spherical flow matching, and delegates feasibility to a combinatorial optimization solver that maps each latent sample to a valid structured action. To improve efficiency, we train the value network directly in the latent space, avoiding repeated solver calls during policy optimization. To address the piecewise-constant and discontinuous value landscape induced by solver-based action selection, we introduce a smoothed Bellman operator that yields stable, well-defined learning targets. Empirically, our approach outperforms state-of-the-art baselines by an average of 20.6\% across a range of challenging combinatorial RL tasks.

Policy-Embedded Graph Expansion: Networked HIV Testing with Diffusion-Driven Network Samples

HIV is a retrovirus that attacks the human immune system and can lead to death without proper treatment. In collaboration with the WHO and Wits University, we study how to improve the efficiency of HIV testing with the goal of eventual deployment, directly supporting progress toward UN Sustainable Development Goal 3.3. While prior work has demonstrated the promise of intelligent algorithms for sequential, network-based HIV testing, existing approaches rely on assumptions that are impractical in our real-world implementations. Here, we study sequential testing on incrementally revealed disease networks and introduce Policy-Embedded Graph Expansion (PEGE), a novel framework that directly embeds a generative distribution over graph expansions into the decision-making policy rather than attempting explicit topological reconstruction. We further propose Dynamics-Driven Branching (DDB), a diffusion-based graph expansion model that supports decision making in PEGE and is designed for data-limited settings where forest structures arise naturally, as in our real-world referral process. Experiments on real HIV transmission networks show that the combined approach (PEGE + DDB) consistently outperforms existing baselines (e.g., 13% improvement in discounted reward and 9% more HIV detections with 25% of the population tested) and explore key tradeoffs that drive decision quality.

Long-horizon Reasoning Agent for Olympiad-Level Mathematical Problem Solving

Large Reasoning Models (LRMs) have expanded the mathematical reasoning frontier through Chain-of-Thought (CoT) techniques and Reinforcement Learning with Verifiable Rewards (RLVR), capable of solving AIME-level problems. However, the performance of LRMs is heavily dependent on the extended reasoning context length. For solving ultra-hard problems like those in the International Mathematical Olympiad (IMO), the required reasoning complexity surpasses the space that an LRM can explore in a single round. Previous works attempt to extend the reasoning context of LRMs but remain prompt-based and built upon proprietary models, lacking systematic structures and training pipelines. Therefore, this paper introduces Intern-S1-MO, a long-horizon math agent that conducts multi-round hierarchical reasoning, composed of an LRM-based multi-agent system including reasoning, summary, and verification. By maintaining a compact memory in the form of lemmas, Intern-S1-MO can more freely explore the lemma-rich reasoning spaces in multiple reasoning stages, thereby breaking through the context constraints for IMO-level math problems. Furthermore, we propose OREAL-H, an RL framework for training the LRM using the online explored trajectories to simultaneously bootstrap the reasoning ability of LRM and elevate the overall performance of Intern-S1-MO. Experiments show that Intern-S1-MO can obtain 26 out of 35 points on the non-geometry problems of IMO2025, matching the performance of silver medalists. It also surpasses the current advanced LRMs on inference benchmarks such as HMMT2025, AIME2025, and CNMO2025. In addition, our agent officially participates in CMO2025 and achieves a score of 102/126 under the judgment of human experts, reaching the gold medal level.

Guided Transfer Learning for Discrete Diffusion Models

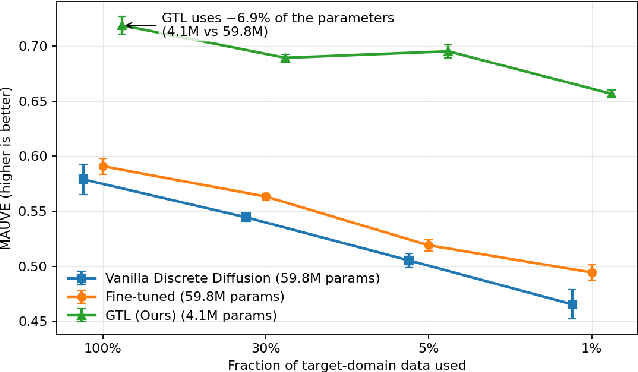
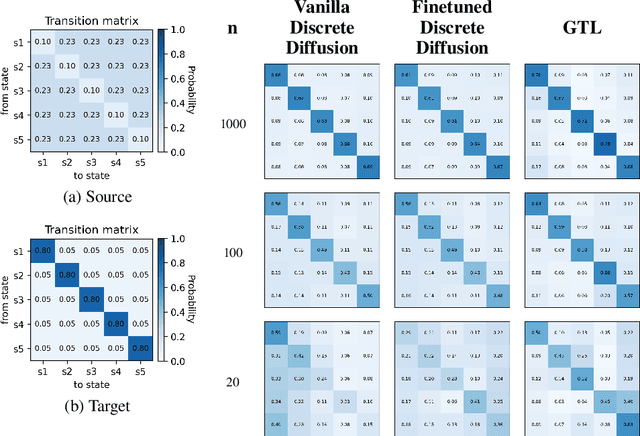
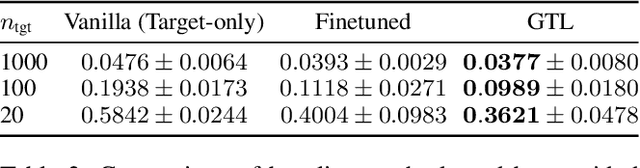
Discrete diffusion models achieve strong performance across language and other discrete domains, providing a powerful alternative to autoregressive models. However, their strong performance relies on large training datasets, which are costly or risky to obtain, especially when adapting to new domains. Transfer learning is the natural way to adapt pretrained discrete diffusion models, but current methods require fine-tuning large diffusion models, which is computationally expensive and often impractical. Building on ratio-based transfer learning for continuous diffusion, we provide Guided Transfer Learning for discrete diffusion models (GTL). This enables sampling from a target distribution without modifying the pretrained denoiser. The same guidance formulation applies to both discrete-time diffusion and continuous-time score-based discrete diffusion, yielding a unified treatment. Guided discrete diffusion often requires many forward passes of the guidance network, which becomes impractical for large vocabularies and long sequences. To address this, we further present an efficient guided sampler that concentrates evaluations on planner-selected positions and top candidate tokens, thus lowering sampling time and computation. This makes guided language modeling practical at scale for large vocabularies and long sequences. We evaluate GTL on sequential data, including synthetic Markov chains and language modeling, and provide empirical analyses of its behavior.

OPV: Outcome-based Process Verifier for Efficient Long Chain-of-Thought Verification

Large language models (LLMs) have achieved significant progress in solving complex reasoning tasks by Reinforcement Learning with Verifiable Rewards (RLVR). This advancement is also inseparable from the oversight automated by reliable verifiers. However, current outcome-based verifiers (OVs) are unable to inspect the unreliable intermediate steps in the long reasoning chains of thought (CoTs). Meanwhile, current process-based verifiers (PVs) have difficulties in reliably detecting errors in the complex long CoTs, limited by the scarcity of high-quality annotations due to the prohibitive costs of human annotations. Therefore, we propose the Outcome-based Process Verifier (OPV), which verifies the rationale process of summarized outcomes from long CoTs to achieve both accurate and efficient verification and enable large-scale annotation. To empower the proposed verifier, we adopt an iterative active learning framework with expert annotations to progressively improve the verification capability of OPV with fewer annotation costs. Specifically, in each iteration, the most uncertain cases of the current best OPV are annotated and then subsequently used to train a new OPV through Rejection Fine-Tuning (RFT) and RLVR for the next round. Extensive experiments demonstrate OPV's superior performance and broad applicability. It achieves new state-of-the-art results on our held-out OPV-Bench, outperforming much larger open-source models such as Qwen3-Max-Preview with an F1 score of 83.1 compared to 76.3. Furthermore, OPV effectively detects false positives within synthetic dataset, closely align with expert assessment. When collaborating with policy models, OPV consistently yields performance gains, e.g., raising the accuracy of DeepSeek-R1-Distill-Qwen-32B from 55.2% to 73.3% on AIME2025 as the compute budget scales.

Generative AI Against Poaching: Latent Composite Flow Matching for Wildlife Conservation

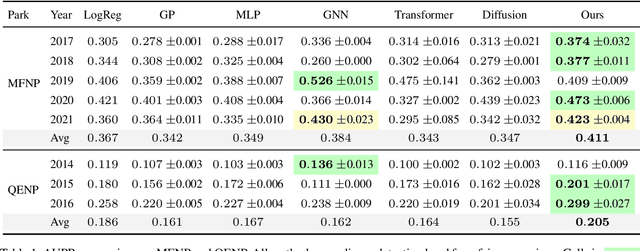
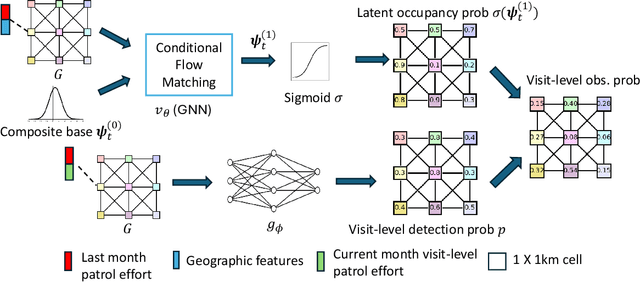
Poaching poses significant threats to wildlife and biodiversity. A valuable step in reducing poaching is to forecast poacher behavior, which can inform patrol planning and other conservation interventions. Existing poaching prediction methods based on linear models or decision trees lack the expressivity to capture complex, nonlinear spatiotemporal patterns. Recent advances in generative modeling, particularly flow matching, offer a more flexible alternative. However, training such models on real-world poaching data faces two central obstacles: imperfect detection of poaching events and limited data. To address imperfect detection, we integrate flow matching with an occupancy-based detection model and train the flow in latent space to infer the underlying occupancy state. To mitigate data scarcity, we adopt a composite flow initialized from a linear-model prediction rather than random noise which is the standard in diffusion models, injecting prior knowledge and improving generalization. Evaluations on datasets from two national parks in Uganda show consistent gains in predictive accuracy.