Normalizing Flows are Capable Generative Models

Normalizing Flows (NFs) are likelihood-based models for continuous inputs. They have demonstrated promising results on both density estimation and generative modeling tasks, but have received relatively little attention in recent years. In this work, we demonstrate that NFs are more powerful than previously believed. We present TarFlow: a simple and scalable architecture that enables highly performant NF models. TarFlow can be thought of as a Transformer-based variant of Masked Autoregressive Flows (MAFs): it consists of a stack of autoregressive Transformer blocks on image patches, alternating the autoregression direction between layers. TarFlow is straightforward to train end-to-end, and capable of directly modeling and generating pixels. We also propose three key techniques to improve sample quality: Gaussian noise augmentation during training, a post training denoising procedure, and an effective guidance method for both class-conditional and unconditional settings. Putting these together, TarFlow sets new state-of-the-art results on likelihood estimation for images, beating the previous best methods by a large margin, and generates samples with quality and diversity comparable to diffusion models, for the first time with a stand-alone NF model. We make our code available at https://github.com/apple/ml-tarflow.

Trivialized Momentum Facilitates Diffusion Generative Modeling on Lie Groups

The generative modeling of data on manifold is an important task, for which diffusion models in flat spaces typically need nontrivial adaptations. This article demonstrates how a technique called `trivialization' can transfer the effectiveness of diffusion models in Euclidean spaces to Lie groups. In particular, an auxiliary momentum variable was algorithmically introduced to help transport the position variable between data distribution and a fixed, easy-to-sample distribution. Normally, this would incur further difficulty for manifold data because momentum lives in a space that changes with the position. However, our trivialization technique creates to a new momentum variable that stays in a simple $\textbf{fixed vector space}$. This design, together with a manifold preserving integrator, simplifies implementation and avoids inaccuracies created by approximations such as projections to tangent space and manifold, which were typically used in prior work, hence facilitating generation with high-fidelity and efficiency. The resulting method achieves state-of-the-art performance on protein and RNA torsion angle generation and sophisticated torus datasets. We also, arguably for the first time, tackle the generation of data on high-dimensional Special Orthogonal and Unitary groups, the latter essential for quantum problems.

React-OT: Optimal Transport for Generating Transition State in Chemical Reactions

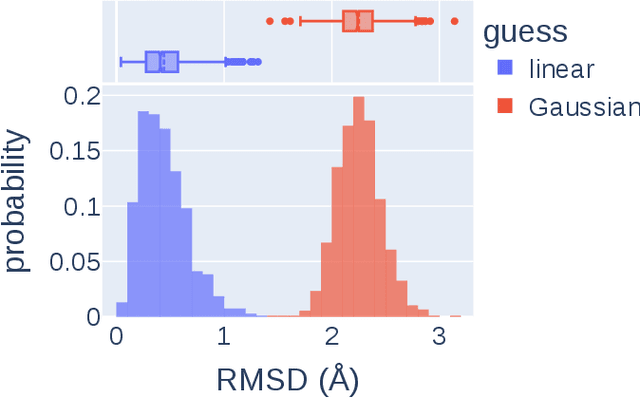
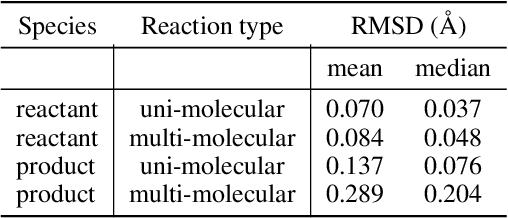
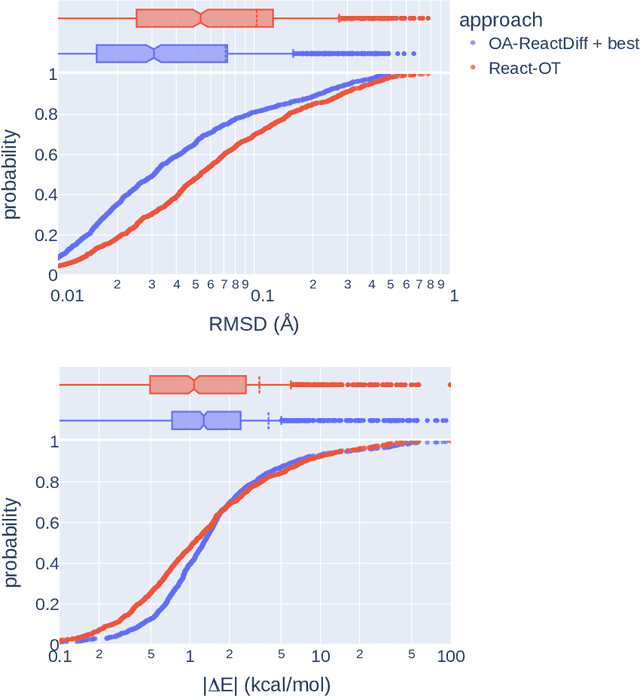
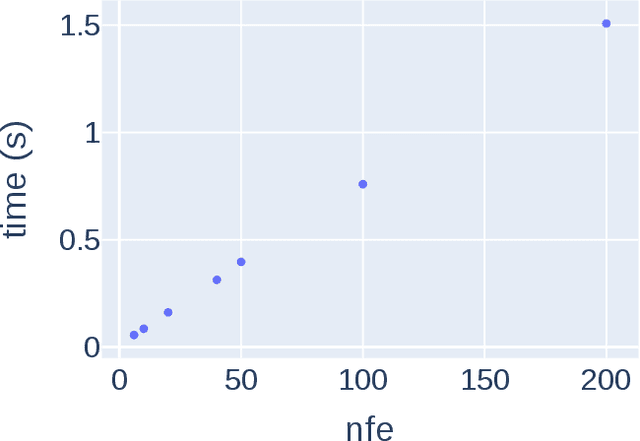
Transition states (TSs) are transient structures that are key in understanding reaction mechanisms and designing catalysts but challenging to be captured in experiments. Alternatively, many optimization algorithms have been developed to search for TSs computationally. Yet the cost of these algorithms driven by quantum chemistry methods (usually density functional theory) is still high, posing challenges for their applications in building large reaction networks for reaction exploration. Here we developed React-OT, an optimal transport approach for generating unique TS structures from reactants and products. React-OT generates highly accurate TS structures with a median structural root mean square deviation (RMSD) of 0.053{\AA} and median barrier height error of 1.06 kcal/mol requiring only 0.4 second per reaction. The RMSD and barrier height error is further improved by roughly 25% through pretraining React-OT on a large reaction dataset obtained with a lower level of theory, GFN2-xTB. We envision the great accuracy and fast inference of React-OT useful in targeting TSs when exploring chemical reactions with unknown mechanisms.

Quantum State Generation with Structure-Preserving Diffusion Model

This article considers the generative modeling of the states of quantum systems, and an approach based on denoising diffusion model is proposed. The key contribution is an algorithmic innovation that respects the physical nature of quantum states. More precisely, the commonly used density matrix representation of mixed-state has to be complex-valued Hermitian, positive semi-definite, and trace one. Generic diffusion models, or other generative methods, may not be able to generate data that strictly satisfy these structural constraints, even if all training data do. To develop a machine learning algorithm that has physics hard-wired in, we leverage the recent development of Mirror Diffusion Model and design a previously unconsidered mirror map, to enable strict structure-preserving generation. Both unconditional generation and conditional generation via classifier-free guidance are experimentally demonstrated efficacious, the latter even enabling the design of new quantum states when generated on unseen labels.

Augmented Bridge Matching

Flow and bridge matching are a novel class of processes which encompass diffusion models. One of the main aspect of their increased flexibility is that these models can interpolate between arbitrary data distributions i.e. they generalize beyond generative modeling and can be applied to learning stochastic (and deterministic) processes of arbitrary transfer tasks between two given distributions. In this paper, we highlight that while flow and bridge matching processes preserve the information of the marginal distributions, they do \emph{not} necessarily preserve the coupling information unless additional, stronger optimality conditions are met. This can be problematic if one aims at preserving the original empirical pairing. We show that a simple modification of the matching process recovers this coupling by augmenting the velocity field (or drift) with the information of the initial sample point. Doing so, we lose the Markovian property of the process but preserve the coupling information between distributions. We illustrate the efficiency of our augmentation in learning mixture of image translation tasks.

Generative Modeling with Phase Stochastic Bridges

Diffusion models (DMs) represent state-of-the-art generative models for continuous inputs. DMs work by constructing a Stochastic Differential Equation (SDE) in the input space (ie, position space), and using a neural network to reverse it. In this work, we introduce a novel generative modeling framework grounded in \textbf{phase space dynamics}, where a phase space is defined as {an augmented space encompassing both position and velocity.} Leveraging insights from Stochastic Optimal Control, we construct a path measure in the phase space that enables efficient sampling. {In contrast to DMs, our framework demonstrates the capability to generate realistic data points at an early stage of dynamics propagation.} This early prediction sets the stage for efficient data generation by leveraging additional velocity information along the trajectory. On standard image generation benchmarks, our model yields favorable performance over baselines in the regime of small Number of Function Evaluations (NFEs). Furthermore, our approach rivals the performance of diffusion models equipped with efficient sampling techniques, underscoring its potential as a new tool generative modeling.

Mirror Diffusion Models for Constrained and Watermarked Generation

Modern successes of diffusion models in learning complex, high-dimensional data distributions are attributed, in part, to their capability to construct diffusion processes with analytic transition kernels and score functions. The tractability results in a simulation-free framework with stable regression losses, from which reversed, generative processes can be learned at scale. However, when data is confined to a constrained set as opposed to a standard Euclidean space, these desirable characteristics appear to be lost based on prior attempts. In this work, we propose Mirror Diffusion Models (MDM), a new class of diffusion models that generate data on convex constrained sets without losing any tractability. This is achieved by learning diffusion processes in a dual space constructed from a mirror map, which, crucially, is a standard Euclidean space. We derive efficient computation of mirror maps for popular constrained sets, such as simplices and $\ell_2$-balls, showing significantly improved performance of MDM over existing methods. For safety and privacy purposes, we also explore constrained sets as a new mechanism to embed invisible but quantitative information (i.e., watermarks) in generated data, for which MDM serves as a compelling approach. Our work brings new algorithmic opportunities for learning tractable diffusion on complex domains.

Deep Momentum Multi-Marginal Schrödinger Bridge

Reconstructing population dynamics using only samples from distributions at coarse time intervals is a crucial challenge. Recent data-driven approaches such as flow-based models or Schr\"odinger Bridge models have demonstrated appealing performance, yet the inferred sample trajectories either fail to account for the underlying stochasticity or are unnecessarily rigid. In this article, we propose $\underline{D}$eep $\underline{M}$omentum Multi-Marginal $\underline{S}$chr\"odinger $\underline{B}$ridge(DMSB), a novel computational framework that learns the smooth measure-valued spline for stochastic systems without violating the position marginal constraints across time. We first extend the scalable mean matching objective used in the state space SB algorithm into the phase space. We next carefully craft a multi-constraint optimization training method based on Bregman Iteration that enables effective phase space means matching training for the high-dimensional dataset. We demonstrate that the resulting training algorithm significantly outperforms baselines on both synthetic datasets and a real-world single-cell RNA sequence dataset.

Deep Generalized Schrödinger Bridge

Mean-Field Game (MFG) serves as a crucial mathematical framework in modeling the collective behavior of individual agents interacting stochastically with a large population. In this work, we aim at solving a challenging class of MFGs in which the differentiability of these interacting preferences may not be available to the solver, and the population is urged to converge exactly to some desired distribution. These setups are, despite being well-motivated for practical purposes, complicated enough to paralyze most (deep) numerical solvers. Nevertheless, we show that Schr\"odinger Bridge - as an entropy-regularized optimal transport model - can be generalized to accepting mean-field structures, hence solving these MFGs. This is achieved via the application of Forward-Backward Stochastic Differential Equations theory, which, intriguingly, leads to a computational framework with a similar structure to Temporal Difference learning. As such, it opens up novel algorithmic connections to Deep Reinforcement Learning that we leverage to facilitate practical training. We show that our proposed objective function provides necessary and sufficient conditions to the mean-field problem. Our method, named Deep Generalized Schr\"odinger Bridge (DeepGSB), not only outperforms prior methods in solving classical population navigation MFGs, but is also capable of solving 1000-dimensional opinion depolarization, setting a new state-of-the-art numerical solver for high-dimensional MFGs. Our code will be made available at https://github.com/ghliu/DeepGSB.

Deep Graphic FBSDEs for Opinion Dynamics Stochastic Control

In this paper, we present a scalable deep learning approach to solve opinion dynamics stochastic optimal control problems with mean field term coupling in the dynamics and cost function. Our approach relies on the probabilistic representation of the solution of the Hamilton-Jacobi-Bellman partial differential equation. Grounded on the nonlinear version of the Feynman-Kac lemma, the solutions of the Hamilton-Jacobi-Bellman partial differential equation are linked to the solution of Forward-Backward Stochastic Differential Equations. These equations can be solved numerically using a novel deep neural network with architecture tailored to the problem in consideration. The resulting algorithm is tested on a polarized opinion consensus experiment. The large-scale (10K) agents experiment validates the scalability and generalizability of our algorithm. The proposed framework opens up the possibility for future applications on extremely large-scale problems.