LabelKAN -- Kolmogorov-Arnold Networks for Inter-Label Learning: Avian Community Learning

Global biodiversity loss is accelerating, prompting international efforts such as the Kunming-Montreal Global Biodiversity Framework (GBF) and the United Nations Sustainable Development Goals to direct resources toward halting species declines. A key challenge in achieving this goal is having access to robust methodologies to understand where species occur and how they relate to each other within broader ecological communities. Recent deep learning-based advances in joint species distribution modeling have shown improved predictive performance, but effectively incorporating community-level learning, taking into account species-species relationships in addition to species-environment relationships, remains an outstanding challenge. We introduce LabelKAN, a novel framework based on Kolmogorov-Arnold Networks (KANs) to learn inter-label connections from predictions of each label. When modeling avian species distributions, LabelKAN achieves substantial gains in predictive performance across the vast majority of species. In particular, our method demonstrates strong improvements for rare and difficult-to-predict species, which are often the most important when setting biodiversity targets under frameworks like GBF. These performance gains also translate to more confident predictions of the species spatial patterns as well as more confident predictions of community structure. We illustrate how the LabelKAN leads to qualitative and quantitative improvements with a focused application on the Great Blue Heron, an emblematic species in freshwater ecosystems that has experienced significant population declines across the United States in recent years. Using the LabelKAN framework, we are able to identify communities and species in New York that will be most sensitive to further declines in Great Blue Heron populations.

Graph Neural Networks are Heuristics

We demonstrate that a single training trajectory can transform a graph neural network into an unsupervised heuristic for combinatorial optimization. Focusing on the Travelling Salesman Problem, we show that encoding global structural constraints as an inductive bias enables a non-autoregressive model to generate solutions via direct forward passes, without search, supervision, or sequential decision-making. At inference time, dropout and snapshot ensembling allow a single model to act as an implicit ensemble, reducing optimality gaps through increased solution diversity. Our results establish that graph neural networks do not require supervised training nor explicit search to be effective. Instead, they can internalize global combinatorial structure and function as strong, learned heuristics. This reframes the role of learning in combinatorial optimization: from augmenting classical algorithms to directly instantiating new heuristics.

Autonomous Materials Exploration by Integrating Automated Phase Identification and AI-Assisted Human Reasoning

Autonomous experimentation holds the potential to accelerate materials development by combining artificial intelligence (AI) with modular robotic platforms to explore extensive combinatorial chemical and processing spaces. Such self-driving laboratories can not only increase the throughput of repetitive experiments, but also incorporate human domain expertise to drive the search towards user-defined objectives, including improved materials performance metrics. We present an autonomous materials synthesis extension to SARA, the Scientific Autonomous Reasoning Agent, utilizing phase information provided by an automated probabilistic phase labeling algorithm to expedite the search for targeted phase regions. By incorporating human input into an expanded SARA-H (SARA with human-in-the-loop) framework, we enhance the efficiency of the underlying reasoning process. Using synthetic benchmarks, we demonstrate the efficiency of our AI implementation and show that the human input can contribute to significant improvement in sampling efficiency. We conduct experimental active learning campaigns using robotic processing of thin-film samples of several oxide material systems, including Bi$_2$O$_3$, SnO$_x$, and Bi-Ti-O, using lateral-gradient laser spike annealing to synthesize and kinetically trap metastable phases. We showcase the utility of human-in-the-loop autonomous experimentation for the Bi-Ti-O system, where we identify extensive processing domains that stabilize $δ$-Bi$_2$O$_3$ and Bi$_2$Ti$_2$O$_7$, explore dwell-dependent ternary oxide phase behavior, and provide evidence confirming predictions that cationic substitutional doping of TiO$_2$ with Bi inhibits the unfavorable transformation of the metastable anatase to the ground-state rutile phase. The autonomous methods we have developed enable the discovery of new materials and new understanding of materials synthesis and properties.

Improving Multislice Electron Ptychography with a Generative Prior

Multislice electron ptychography (MEP) is an inverse imaging technique that computationally reconstructs the highest-resolution images of atomic crystal structures from diffraction patterns. Available algorithms often solve this inverse problem iteratively but are both time consuming and produce suboptimal solutions due to their ill-posed nature. We develop MEP-Diffusion, a diffusion model trained on a large database of crystal structures specifically for MEP to augment existing iterative solvers. MEP-Diffusion is easily integrated as a generative prior into existing reconstruction methods via Diffusion Posterior Sampling (DPS). We find that this hybrid approach greatly enhances the quality of the reconstructed 3D volumes, achieving a 90.50% improvement in SSIM over existing methods.

HeuriGym: An Agentic Benchmark for LLM-Crafted Heuristics in Combinatorial Optimization

While Large Language Models (LLMs) have demonstrated significant advancements in reasoning and agent-based problem-solving, current evaluation methodologies fail to adequately assess their capabilities: existing benchmarks either rely on closed-ended questions prone to saturation and memorization, or subjective comparisons that lack consistency and rigor. In this work, we introduce HeuriGym, an agentic framework designed for evaluating heuristic algorithms generated by LLMs for combinatorial optimization problems, characterized by clearly defined objectives and expansive solution spaces. HeuriGym empowers LLMs to propose heuristics, receive evaluative feedback via code execution, and iteratively refine their solutions. We evaluate nine state-of-the-art models on nine problems across domains such as computer systems, logistics, and biology, exposing persistent limitations in tool use, planning, and adaptive reasoning. To quantify performance, we propose the Quality-Yield Index (QYI), a metric that captures both solution pass rate and quality. Even top models like GPT-o4-mini-high and Gemini-2.5-Pro attain QYI scores of only 0.6, well below the expert baseline of 1. Our open-source benchmark aims to guide the development of LLMs toward more effective and realistic problem-solving in scientific and engineering domains.

FEAT: Free energy Estimators with Adaptive Transport

We present Free energy Estimators with Adaptive Transport (FEAT), a novel framework for free energy estimation -- a critical challenge across scientific domains. FEAT leverages learned transports implemented via stochastic interpolants and provides consistent, minimum-variance estimators based on escorted Jarzynski equality and controlled Crooks theorem, alongside variational upper and lower bounds on free energy differences. Unifying equilibrium and non-equilibrium methods under a single theoretical framework, FEAT establishes a principled foundation for neural free energy calculations. Experimental validation on toy examples, molecular simulations, and quantum field theory demonstrates improvements over existing learning-based methods.

Unsupervised Learning for Quadratic Assignment

We introduce PLUME search, a data-driven framework that enhances search efficiency in combinatorial optimization through unsupervised learning. Unlike supervised or reinforcement learning, PLUME search learns directly from problem instances using a permutation-based loss with a non-autoregressive approach. We evaluate its performance on the quadratic assignment problem, a fundamental NP-hard problem that encompasses various combinatorial optimization problems. Experimental results demonstrate that PLUME search consistently improves solution quality. Furthermore, we study the generalization behavior and show that the learned model generalizes across different densities and sizes.

Large Language Models Are Innate Crystal Structure Generators

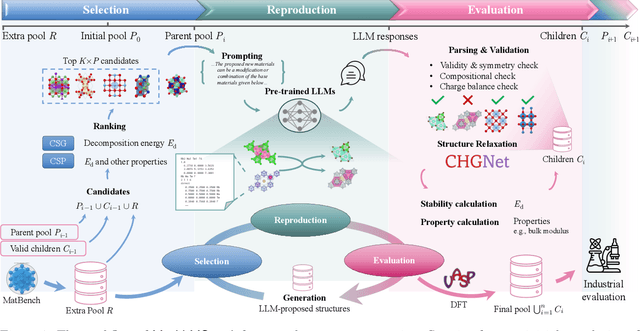
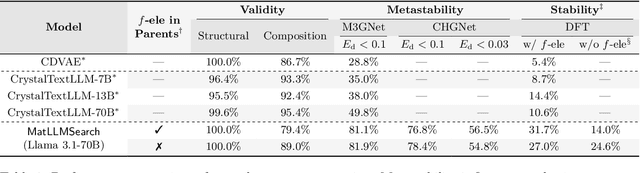
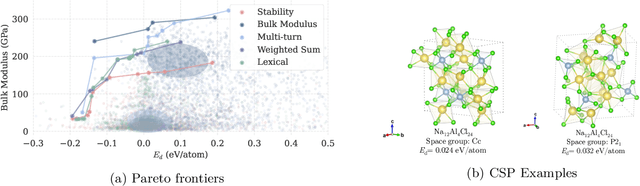
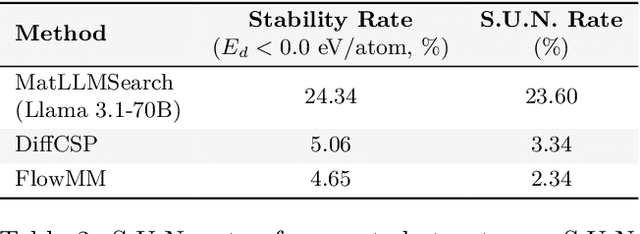
Crystal structure generation is fundamental to materials discovery, enabling the prediction of novel materials with desired properties. While existing approaches leverage Large Language Models (LLMs) through extensive fine-tuning on materials databases, we show that pre-trained LLMs can inherently generate stable crystal structures without additional training. Our novel framework MatLLMSearch integrates pre-trained LLMs with evolutionary search algorithms, achieving a 78.38% metastable rate validated by machine learning interatomic potentials and 31.7% DFT-verified stability via quantum mechanical calculations, outperforming specialized models such as CrystalTextLLM. Beyond crystal structure generation, we further demonstrate that our framework can be readily adapted to diverse materials design tasks, including crystal structure prediction and multi-objective optimization of properties such as deformation energy and bulk modulus, all without fine-tuning. These results establish pre-trained LLMs as versatile and effective tools for materials discovery, opening up new venues for crystal structure generation with reduced computational overhead and broader accessibility.

PhantomWiki: On-Demand Datasets for Reasoning and Retrieval Evaluation

High-quality benchmarks are essential for evaluating reasoning and retrieval capabilities of large language models (LLMs). However, curating datasets for this purpose is not a permanent solution as they are prone to data leakage and inflated performance results. To address these challenges, we propose PhantomWiki: a pipeline to generate unique, factually consistent document corpora with diverse question-answer pairs. Unlike prior work, PhantomWiki is neither a fixed dataset, nor is it based on any existing data. Instead, a new PhantomWiki instance is generated on demand for each evaluation. We vary the question difficulty and corpus size to disentangle reasoning and retrieval capabilities respectively, and find that PhantomWiki datasets are surprisingly challenging for frontier LLMs. Thus, we contribute a scalable and data leakage-resistant framework for disentangled evaluation of reasoning, retrieval, and tool-use abilities. Our code is available at https://github.com/kilian-group/phantom-wiki.

AlphaNet: Scaling Up Local Frame-based Atomistic Foundation Model

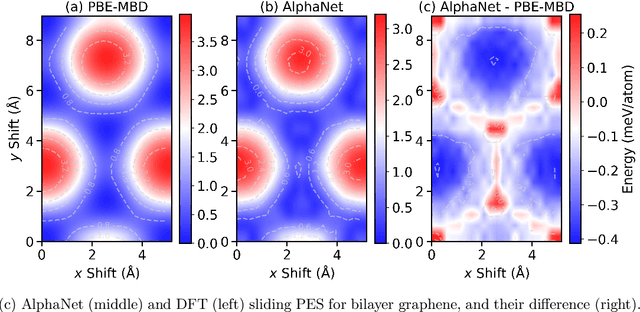
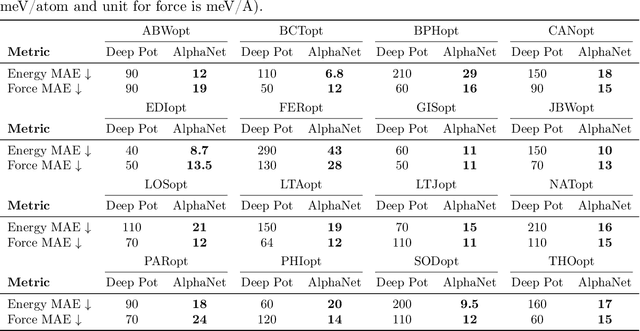
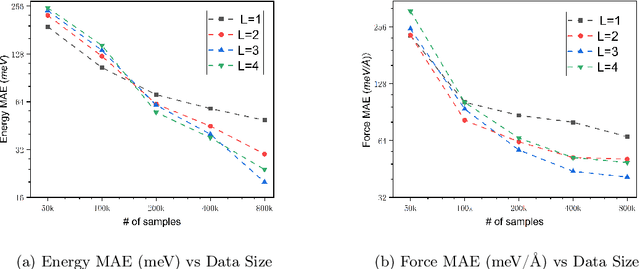
We present AlphaNet, a local frame-based equivariant model designed to achieve both accurate and efficient simulations for atomistic systems. Recently, machine learning force fields (MLFFs) have gained prominence in molecular dynamics simulations due to their advantageous efficiency-accuracy balance compared to classical force fields and quantum mechanical calculations, alongside their transferability across various systems. Despite the advancements in improving model accuracy, the efficiency and scalability of MLFFs remain significant obstacles in practical applications. AlphaNet enhances computational efficiency and accuracy by leveraging the local geometric structures of atomic environments through the construction of equivariant local frames and learnable frame transitions. We substantiate the efficacy of AlphaNet across diverse datasets, including defected graphene, formate decomposition, zeolites, and surface reactions. AlphaNet consistently surpasses well-established models, such as NequIP and DeepPot, in terms of both energy and force prediction accuracy. Notably, AlphaNet offers one of the best trade-offs between computational efficiency and accuracy among existing models. Moreover, AlphaNet exhibits scalability across a broad spectrum of system and dataset sizes, affirming its versatility.