The impact of fine tuning in LLaMA on hallucinations for named entity extraction in legal documentation

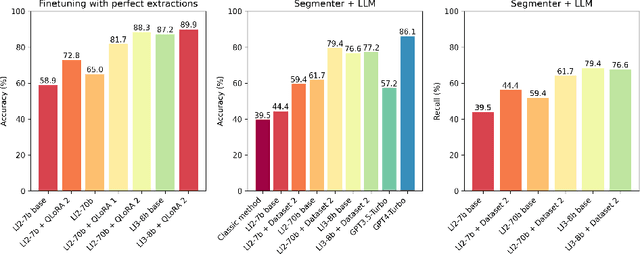
The extraction of information about traffic accidents from legal documents is crucial for quantifying insurance company costs. Extracting entities such as percentages of physical and/or psychological disability and the involved compensation amounts is a challenging process, even for experts, due to the subtle arguments and reasoning in the court decision. A two-step procedure is proposed: first, segmenting the document identifying the most relevant segments, and then extracting the entities. For text segmentation, two methodologies are compared: a classic method based on regular expressions and a second approach that divides the document into blocks of n-tokens, which are then vectorized using multilingual models for semantic searches (text-embedding-ada-002/MiniLM-L12-v2 ). Subsequently, large language models (LLaMA-2 7b, 70b, LLaMA-3 8b, and GPT-4 Turbo) are applied with prompting to the selected segments for entity extraction. For the LLaMA models, fine-tuning is performed using LoRA. LLaMA-2 7b, even with zero temperature, shows a significant number of hallucinations in extractions which are an important contention point for named entity extraction. This work shows that these hallucinations are substantially reduced after finetuning the model. The performance of the methodology based on segment vectorization and subsequent use of LLMs significantly surpasses the classic method which achieves an accuracy of 39.5%. Among open-source models, LLaMA-2 70B with finetuning achieves the highest accuracy 79.4%, surpassing its base version 61.7%. Notably, the base LLaMA-3 8B model already performs comparably to the finetuned LLaMA-2 70B model, achieving 76.6%, highlighting the rapid progress in model development. Meanwhile, GPT-4 Turbo achieves the highest accuracy at 86.1%.

Path Integral Optimiser: Global Optimisation via Neural Schrödinger-Föllmer Diffusion

We present an early investigation into the use of neural diffusion processes for global optimisation, focusing on Zhang et al.'s Path Integral Sampler. One can use the Boltzmann distribution to formulate optimization as solving a Schr\"odinger bridge sampling problem, then apply Girsanov's theorem with a simple (single-point) prior to frame it in stochastic control terms, and compute the solution's integral terms via a neural approximation (a Fourier MLP). We provide theoretical bounds for this optimiser, results on toy optimisation tasks, and a summary of the stochastic theory motivating the model. Ultimately, we found the optimiser to display promising per-step performance at optimisation tasks between 2 and 1,247 dimensions, but struggle to explore higher-dimensional spaces when faced with a 15.9k parameter model, indicating a need for work on adaptation in such environments.

RNE: a plug-and-play framework for diffusion density estimation and inference-time control

In this paper, we introduce the Radon-Nikodym Estimator (RNE), a flexible, plug-and-play framework for diffusion inference-time density estimation and control, based on the concept of the density ratio between path distributions. RNE connects and unifies a variety of existing density estimation and inference-time control methods under a single and intuitive perspective, stemming from basic variational inference and probabilistic principles therefore offering both theoretical clarity and practical versatility. Experiments demonstrate that RNE achieves promising performances in diffusion density estimation and inference-time control tasks, including annealing, composition of diffusion models, and reward-tilting.

FEAT: Free energy Estimators with Adaptive Transport

We present Free energy Estimators with Adaptive Transport (FEAT), a novel framework for free energy estimation -- a critical challenge across scientific domains. FEAT leverages learned transports implemented via stochastic interpolants and provides consistent, minimum-variance estimators based on escorted Jarzynski equality and controlled Crooks theorem, alongside variational upper and lower bounds on free energy differences. Unifying equilibrium and non-equilibrium methods under a single theoretical framework, FEAT establishes a principled foundation for neural free energy calculations. Experimental validation on toy examples, molecular simulations, and quantum field theory demonstrates improvements over existing learning-based methods.

Debiasing Guidance for Discrete Diffusion with Sequential Monte Carlo

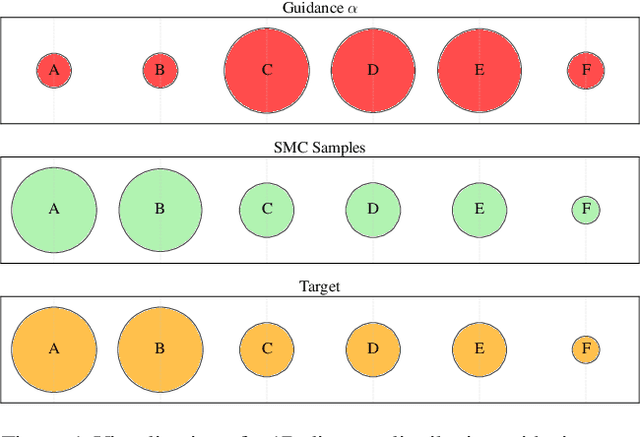
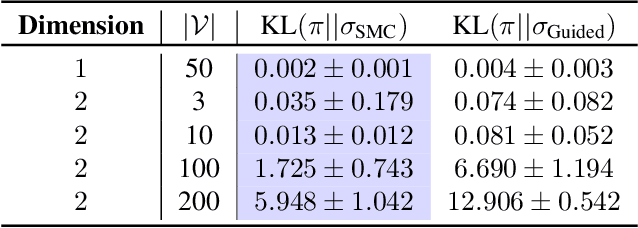
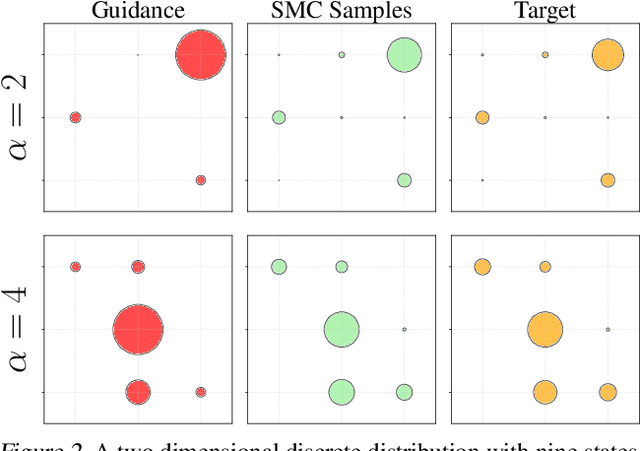
Discrete diffusion models are a class of generative models that produce samples from an approximated data distribution within a discrete state space. Often, there is a need to target specific regions of the data distribution. Current guidance methods aim to sample from a distribution with mass proportional to $p_0(x_0) p(\zeta|x_0)^\alpha$ but fail to achieve this in practice. We introduce a Sequential Monte Carlo algorithm that generates unbiasedly from this target distribution, utilising the learnt unconditional and guided process. We validate our approach on low-dimensional distributions, controlled images and text generations. For text generation, our method provides strong control while maintaining low perplexity compared to guidance-based approaches.

No Trick, No Treat: Pursuits and Challenges Towards Simulation-free Training of Neural Samplers

We consider the sampling problem, where the aim is to draw samples from a distribution whose density is known only up to a normalization constant. Recent breakthroughs in generative modeling to approximate a high-dimensional data distribution have sparked significant interest in developing neural network-based methods for this challenging problem. However, neural samplers typically incur heavy computational overhead due to simulating trajectories during training. This motivates the pursuit of simulation-free training procedures of neural samplers. In this work, we propose an elegant modification to previous methods, which allows simulation-free training with the help of a time-dependent normalizing flow. However, it ultimately suffers from severe mode collapse. On closer inspection, we find that nearly all successful neural samplers rely on Langevin preconditioning to avoid mode collapsing. We systematically analyze several popular methods with various objective functions and demonstrate that, in the absence of Langevin preconditioning, most of them fail to adequately cover even a simple target. Finally, we draw attention to a strong baseline by combining the state-of-the-art MCMC method, Parallel Tempering (PT), with an additional generative model to shed light on future explorations of neural samplers.

Iterative Importance Fine-tuning of Diffusion Models

Diffusion models are an important tool for generative modelling, serving as effective priors in applications such as imaging and protein design. A key challenge in applying diffusion models for downstream tasks is efficiently sampling from resulting posterior distributions, which can be addressed using the $h$-transform. This work introduces a self-supervised algorithm for fine-tuning diffusion models by estimating the $h$-transform, enabling amortised conditional sampling. Our method iteratively refines the $h$-transform using a synthetic dataset resampled with path-based importance weights. We demonstrate the effectiveness of this framework on class-conditional sampling and reward fine-tuning for text-to-image diffusion models.

Beyond ELBOs: A Large-Scale Evaluation of Variational Methods for Sampling

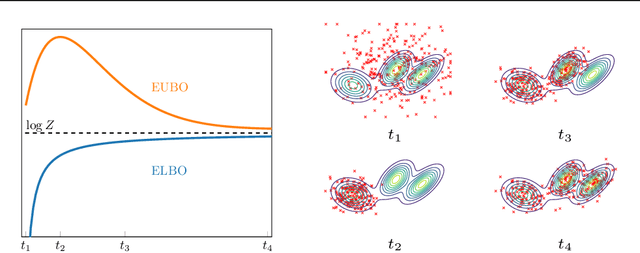
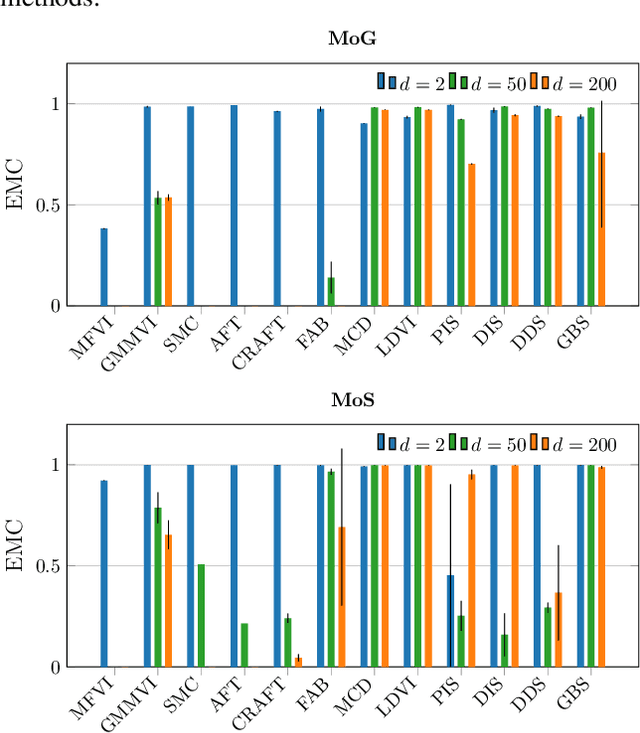
Monte Carlo methods, Variational Inference, and their combinations play a pivotal role in sampling from intractable probability distributions. However, current studies lack a unified evaluation framework, relying on disparate performance measures and limited method comparisons across diverse tasks, complicating the assessment of progress and hindering the decision-making of practitioners. In response to these challenges, our work introduces a benchmark that evaluates sampling methods using a standardized task suite and a broad range of performance criteria. Moreover, we study existing metrics for quantifying mode collapse and introduce novel metrics for this purpose. Our findings provide insights into strengths and weaknesses of existing sampling methods, serving as a valuable reference for future developments. The code is publicly available here.

Improving Antibody Design with Force-Guided Sampling in Diffusion Models

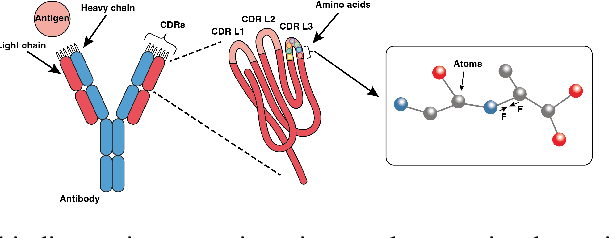
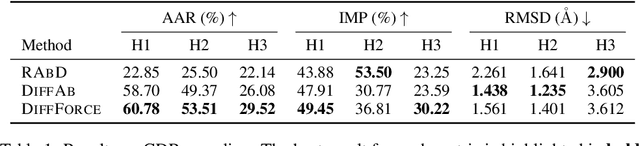
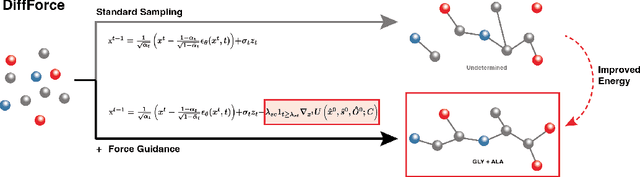
Antibodies, crucial for immune defense, primarily rely on complementarity-determining regions (CDRs) to bind and neutralize antigens, such as viruses. The design of these CDRs determines the antibody's affinity and specificity towards its target. Generative models, particularly denoising diffusion probabilistic models (DDPMs), have shown potential to advance the structure-based design of CDR regions. However, only a limited dataset of bound antibody-antigen structures is available, and generalization to out-of-distribution interfaces remains a challenge. Physics based force-fields, which approximate atomic interactions, offer a coarse but universal source of information to better mold designs to target interfaces. Integrating this foundational information into diffusion models is, therefore, highly desirable. Here, we propose a novel approach to enhance the sampling process of diffusion models by integrating force field energy-based feedback. Our model, DiffForce, employs forces to guide the diffusion sampling process, effectively blending the two distributions. Through extensive experiments, we demonstrate that our method guides the model to sample CDRs with lower energy, enhancing both the structure and sequence of the generated antibodies.

DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.