Solving Inverse Problems with Flow-based Models via Model Predictive Control

Flow-based generative models provide strong unconditional priors for inverse problems, but guiding their dynamics for conditional generation remains challenging. Recent work casts training-free conditional generation in flow models as an optimal control problem; however, solving the resulting trajectory optimisation is computationally and memory intensive, requiring differentiation through the flow dynamics or adjoint solves. We propose MPC-Flow, a model predictive control framework that formulates inverse problem solving with flow-based generative models as a sequence of control sub-problems, enabling practical optimal control-based guidance at inference time. We provide theoretical guarantees linking MPC-Flow to the underlying optimal control objective and show how different algorithmic choices yield a spectrum of guidance algorithms, including regimes that avoid backpropagation through the generative model trajectory. We evaluate MPC-Flow on benchmark image restoration tasks, spanning linear and non-linear settings such as in-painting, deblurring, and super-resolution, and demonstrate strong performance and scalability to massive state-of-the-art architectures via training-free guidance of FLUX.2 (32B) in a quantised setting on consumer hardware.

Supervised Guidance Training for Infinite-Dimensional Diffusion Models

Score-based diffusion models have recently been extended to infinite-dimensional function spaces, with uses such as inverse problems arising from partial differential equations. In the Bayesian formulation of inverse problems, the aim is to sample from a posterior distribution over functions obtained by conditioning a prior on noisy observations. While diffusion models provide expressive priors in function space, the theory of conditioning them to sample from the posterior remains open. We address this, assuming that either the prior lies in the Cameron-Martin space, or is absolutely continuous with respect to a Gaussian measure. We prove that the models can be conditioned using an infinite-dimensional extension of Doob's $h$-transform, and that the conditional score decomposes into an unconditional score and a guidance term. As the guidance term is intractable, we propose a simulation-free score matching objective (called Supervised Guidance Training) enabling efficient and stable posterior sampling. We illustrate the theory with numerical examples on Bayesian inverse problems in function spaces. In summary, our work offers the first function-space method for fine-tuning trained diffusion models to accurately sample from a posterior.

Learning Regularization Functionals for Inverse Problems: A Comparative Study

In recent years, a variety of learned regularization frameworks for solving inverse problems in imaging have emerged. These offer flexible modeling together with mathematical insights. The proposed methods differ in their architectural design and training strategies, making direct comparison challenging due to non-modular implementations. We address this gap by collecting and unifying the available code into a common framework. This unified view allows us to systematically compare the approaches and highlight their strengths and limitations, providing valuable insights into their future potential. We also provide concise descriptions of each method, complemented by practical guidelines.

Learning Binary Sampling Patterns for Single-Pixel Imaging using Bilevel Optimisation

Single-Pixel Imaging enables reconstructing objects using a single detector through sequential illuminations with structured light patterns. We propose a bilevel optimisation method for learning task-specific, binary illumination patterns, optimised for applications like single-pixel fluorescence microscopy. We address the non-differentiable nature of binary pattern optimisation using the Straight-Through Estimator and leveraging a Total Deep Variation regulariser in the bilevel formulation. We demonstrate our method on the CytoImageNet microscopy dataset and show that learned patterns achieve superior reconstruction performance compared to baseline methods, especially in highly undersampled regimes.

Deep Learning Based Reconstruction Methods for Electrical Impedance Tomography

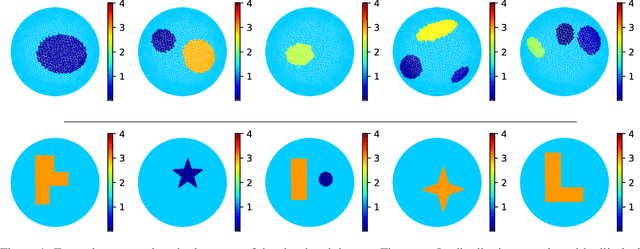
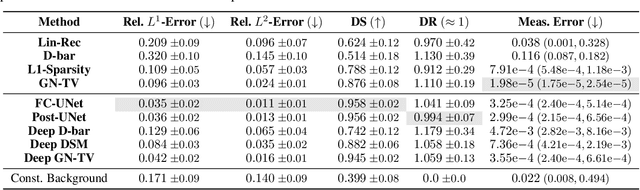
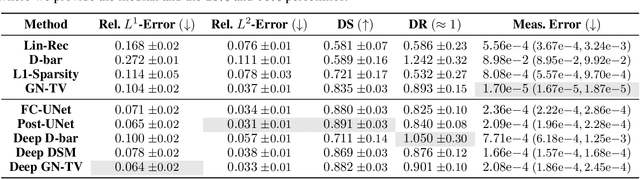
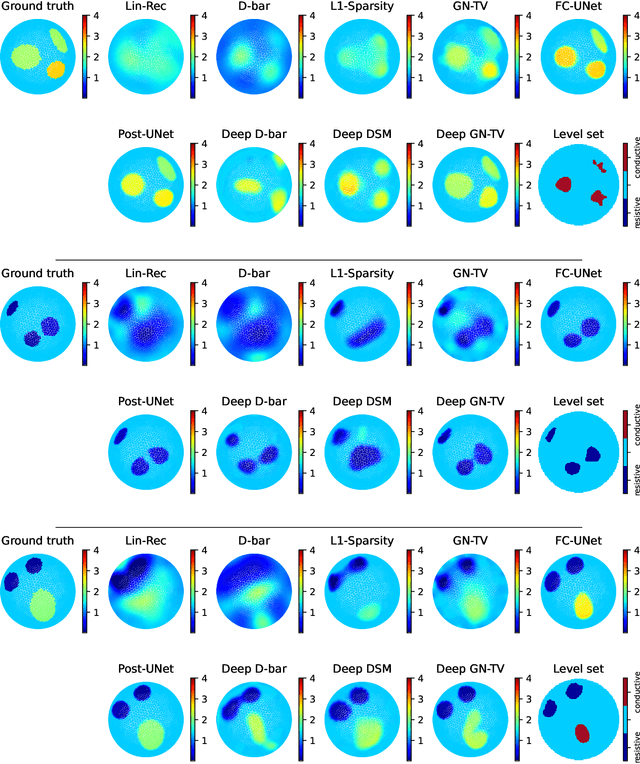
Electrical Impedance Tomography (EIT) is a powerful imaging modality widely used in medical diagnostics, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of the concerned object from the voltage measurements taken on its boundary. This problem is severely ill-posed, and requires advanced computational approaches for accurate and reliable image reconstruction. Recent innovations in both model-based reconstruction and deep learning have driven significant progress in the field. In this review, we explore learned reconstruction methods that employ deep neural networks for solving the EIT inverse problem. The discussion focuses on the complete electrode model, one popular mathematical model for real-world applications of EIT. We compare a wide variety of learned approaches, including fully-learned, post-processing and learned iterative methods, with several conventional model-based reconstruction techniques, e.g., sparsity regularization, regularized Gauss-Newton iteration and level set method. The evaluation is based on three datasets: a simulated dataset of ellipses, an out-of-distribution simulated dataset, and the KIT4 dataset, including real-world measurements. Our results demonstrate that learned methods outperform model-based methods for in-distribution data but face challenges in generalization, where hybrid methods exhibit a good balance of accuracy and adaptability.

Iterative Importance Fine-tuning of Diffusion Models

Diffusion models are an important tool for generative modelling, serving as effective priors in applications such as imaging and protein design. A key challenge in applying diffusion models for downstream tasks is efficiently sampling from resulting posterior distributions, which can be addressed using the $h$-transform. This work introduces a self-supervised algorithm for fine-tuning diffusion models by estimating the $h$-transform, enabling amortised conditional sampling. Our method iteratively refines the $h$-transform using a synthetic dataset resampled with path-based importance weights. We demonstrate the effectiveness of this framework on class-conditional sampling and reward fine-tuning for text-to-image diffusion models.

Plug-and-Play Half-Quadratic Splitting for Ptychography

Ptychography is a coherent diffraction imaging method that uses phase retrieval techniques to reconstruct complex-valued images. It achieves this by sequentially illuminating overlapping regions of a sample with a coherent beam and recording the diffraction pattern. Although this addresses traditional imaging system challenges, it is computationally intensive and highly sensitive to noise, especially with reduced illumination overlap. Data-driven regularisation techniques have been applied in phase retrieval to improve reconstruction quality. In particular, plug-and-play (PnP) offers flexibility by integrating data-driven denoisers as implicit priors. In this work, we propose a half-quadratic splitting framework for using PnP and other data-driven priors for ptychography. We evaluate our method both on natural images and real test objects to validate its effectiveness for ptychographic image reconstruction.

DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.

Convergence Properties of Score-Based Models using Graduated Optimisation for Linear Inverse Problems

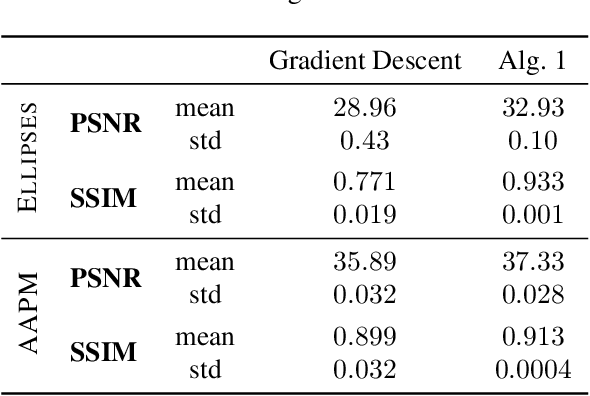
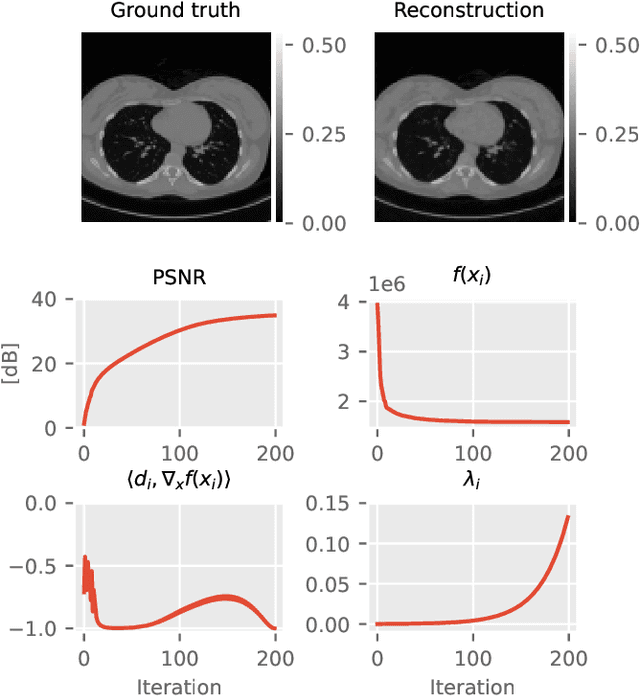
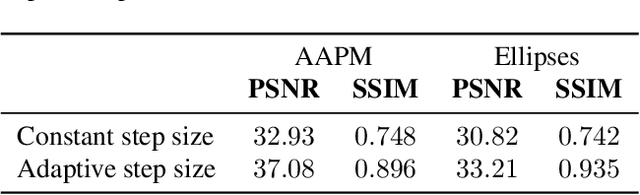
The incorporation of generative models as regularisers within variational formulations for inverse problems has proven effective across numerous image reconstruction tasks. However, the resulting optimisation problem is often non-convex and challenging to solve. In this work, we show that score-based generative models (SGMs) can be used in a graduated optimisation framework to solve inverse problems. We show that the resulting graduated non-convexity flow converge to stationary points of the original problem and provide a numerical convergence analysis of a 2D toy example. We further provide experiments on computed tomography image reconstruction, where we show that this framework is able to recover high-quality images, independent of the initial value. The experiments highlight the potential of using SGMs in graduated optimisation frameworks.

Steerable Conditional Diffusion for Out-of-Distribution Adaptation in Imaging Inverse Problems

Denoising diffusion models have emerged as the go-to framework for solving inverse problems in imaging. A critical concern regarding these models is their performance on out-of-distribution (OOD) tasks, which remains an under-explored challenge. Realistic reconstructions inconsistent with the measured data can be generated, hallucinating image features that are uniquely present in the training dataset. To simultaneously enforce data-consistency and leverage data-driven priors, we introduce a novel sampling framework called Steerable Conditional Diffusion. This framework adapts the denoising network specifically to the available measured data. Utilising our proposed method, we achieve substantial enhancements in OOD performance across diverse imaging modalities, advancing the robust deployment of denoising diffusion models in real-world applications.