Self-Supervised Denoiser Framework

Reconstructing images using Computed Tomography (CT) in an industrial context leads to specific challenges that differ from those encountered in other areas, such as clinical CT. Indeed, non-destructive testing with industrial CT will often involve scanning multiple similar objects while maintaining high throughput, requiring short scanning times, which is not a relevant concern in clinical CT. Under-sampling the tomographic data (sinograms) is a natural way to reduce the scanning time at the cost of image quality since the latter depends on the number of measurements. In such a scenario, post-processing techniques are required to compensate for the image artifacts induced by the sinogram sparsity. We introduce the Self-supervised Denoiser Framework (SDF), a self-supervised training method that leverages pre-training on highly sampled sinogram data to enhance the quality of images reconstructed from undersampled sinogram data. The main contribution of SDF is that it proposes to train an image denoiser in the sinogram space by setting the learning task as the prediction of one sinogram subset from another. As such, it does not require ground-truth image data, leverages the abundant data modality in CT, the sinogram, and can drastically enhance the quality of images reconstructed from a fraction of the measurements. We demonstrate that SDF produces better image quality, in terms of peak signal-to-noise ratio, than other analytical and self-supervised frameworks in both 2D fan-beam or 3D cone-beam CT settings. Moreover, we show that the enhancement provided by SDF carries over when fine-tuning the image denoiser on a few examples, making it a suitable pre-training technique in a context where there is little high-quality image data. Our results are established on experimental datasets, making SDF a strong candidate for being the building block of foundational image-enhancement models in CT.

Model-based reconstructions for quantitative imaging in photoacoustic tomography

The reconstruction task in photoacoustic tomography can vary a lot depending on measured targets, geometry, and especially the quantity we want to recover. Specifically, as the signal is generated due to the coupling of light and sound by the photoacoustic effect, we have the possibility to recover acoustic as well as optical tissue parameters. This is referred to as quantitative imaging, i.e, correct recovery of physical parameters and not just a qualitative image. In this chapter, we aim to give an overview on established reconstruction techniques in photoacoustic tomography. We start with modelling of the optical and acoustic phenomena, necessary for a reliable recovery of quantitative values. Furthermore, we give an overview of approaches for the tomographic reconstruction problem with an emphasis on the recovery of quantitative values, from direct and fast analytic approaches to computationally involved optimisation based techniques and recent data-driven approaches.

Inverse Problems with Learned Forward Operators

Solving inverse problems requires knowledge of the forward operator, but accurate models can be computationally expensive and hence cheaper variants are desired that do not compromise reconstruction quality. This chapter reviews reconstruction methods in inverse problems with learned forward operators that follow two different paradigms. The first one is completely agnostic to the forward operator and learns its restriction to the subspace spanned by the training data. The framework of regularisation by projection is then used to find a reconstruction. The second one uses a simplified model of the physics of the measurement process and only relies on the training data to learn a model correction. We present the theory of these two approaches and compare them numerically. A common theme emerges: both methods require, or at least benefit from, training data not only for the forward operator, but also for its adjoint.

Electrical Impedance Tomography: A Fair Comparative Study on Deep Learning and Analytic-based Approaches

Electrical Impedance Tomography (EIT) is a powerful imaging technique with diverse applications, e.g., medical diagnosis, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of an object from measurements taken on its boundary. It is severely ill-posed, necessitating advanced computational methods for accurate image reconstructions. Recent years have witnessed significant progress, driven by innovations in analytic-based approaches and deep learning. This review explores techniques for solving the EIT inverse problem, focusing on the interplay between contemporary deep learning-based strategies and classical analytic-based methods. Four state-of-the-art deep learning algorithms are rigorously examined, harnessing the representational capabilities of deep neural networks to reconstruct intricate conductivity distributions. In parallel, two analytic-based methods, rooted in mathematical formulations and regularisation techniques, are dissected for their strengths and limitations. These methodologies are evaluated through various numerical experiments, encompassing diverse scenarios that reflect real-world complexities. A suite of performance metrics is employed to assess the efficacy of these methods. These metrics collectively provide a nuanced understanding of the methods' ability to capture essential features and delineate complex conductivity patterns. One novel feature of the study is the incorporation of variable conductivity scenarios, introducing a level of heterogeneity that mimics textured inclusions. This departure from uniform conductivity assumptions mimics realistic scenarios where tissues or materials exhibit spatially varying electrical properties. Exploring how each method responds to such variable conductivity scenarios opens avenues for understanding their robustness and adaptability.

Convergent regularization in inverse problems and linear plug-and-play denoisers

Plug-and-play (PnP) denoising is a popular iterative framework for solving imaging inverse problems using off-the-shelf image denoisers. Their empirical success has motivated a line of research that seeks to understand the convergence of PnP iterates under various assumptions on the denoiser. While a significant amount of research has gone into establishing the convergence of the PnP iteration for different regularity conditions on the denoisers, not much is known about the asymptotic properties of the converged solution as the noise level in the measurement tends to zero, i.e., whether PnP methods are provably convergent regularization schemes under reasonable assumptions on the denoiser. This paper serves two purposes: first, we provide an overview of the classical regularization theory in inverse problems and survey a few notable recent data-driven methods that are provably convergent regularization schemes. We then continue to discuss PnP algorithms and their established convergence guarantees. Subsequently, we consider PnP algorithms with linear denoisers and propose a novel spectral filtering technique to control the strength of regularization arising from the denoiser. Further, by relating the implicit regularization of the denoiser to an explicit regularization functional, we rigorously show that PnP with linear denoisers leads to a convergent regularization scheme. More specifically, we prove that in the limit as the noise vanishes, the PnP reconstruction converges to the minimizer of a regularization potential subject to the solution satisfying the noiseless operator equation. The theoretical analysis is corroborated by numerical experiments for the classical inverse problem of tomographic image reconstruction.

Domain independent post-processing with graph U-nets: Applications to Electrical Impedance Tomographic Imaging

Reconstruction of tomographic images from boundary measurements requires flexibility with respect to target domains. For instance, when the system equations are modeled by partial differential equations the reconstruction is usually done on finite element (FE) meshes, allowing for flexible geometries. Thus, any processing of the obtained reconstructions should be ideally done on the FE mesh as well. For this purpose, we extend the hugely successful U-Net architecture that is limited to rectangular pixel or voxel domains to an equivalent that works flexibly on FE meshes. To achieve this, the FE mesh is converted into a graph and we formulate a graph U-Net with a new cluster pooling and unpooling on the graph that mimics the classic neighborhood based max-pooling. We demonstrate effectiveness and flexibility of the graph U-Net for improving reconstructions from electrical impedance tomographic (EIT) measurements, a nonlinear and highly ill-posed inverse problem. The performance is evaluated for simulated data and from three measurement devices with different measurement geometries and instrumentations. We successfully show that such networks can be trained with a simple two-dimensional simulated training set and generalize to very different domains, including measurements from a three-dimensional device and subsequent 3D reconstructions.

Joint Activity Detection and Channel Estimation for Clustered Massive Machine Type Communications

Compressed sensing multi-user detection (CS-MUD) algorithms play a key role in optimizing grant-free (GF) non-orthogonal multiple access (NOMA) for massive machine-type communications (mMTC). However, current CS-MUD algorithms cannot be efficiently parallelized, which results in computationally expensive implementations of joint activity detection and channel estimation (JADCE) as the number of deployed machine-type devices (MTDs) increases. To address this, the present work proposes novel JADCE algorithms that can be applied in parallel for different clusters of MTDs by exploiting the structure of the pilot sequences. These are the approximation error method (AEM)-alternating direction method of multipliers (ADMM) and AEM-sparse Bayesian learning (SBL). Results presented in terms of the normalized mean square error and the probability of miss detection evince comparable performance to the conventional algorithms. However, both AEM-ADMM and AEM-SBL algorithms have significantly reduced computational complexity and run-times, thus, increasing network scalability.

Model-corrected learned primal-dual models for fast limited-view photoacoustic tomography

Learned iterative reconstructions hold great promise to accelerate tomographic imaging with empirical robustness to model perturbations. Nevertheless, an adoption for photoacoustic tomography is hindered by the need to repeatedly evaluate the computational expensive forward model. Computational feasibility can be obtained by the use of fast approximate models, but a need to compensate model errors arises. In this work we advance the methodological and theoretical basis for model corrections in learned image reconstructions by embedding the model correction in a learned primal-dual framework. Here, the model correction is jointly learned in data space coupled with a learned updating operator in image space within an unrolled end-to-end learned iterative reconstruction approach. The proposed formulation allows an extension to a primal-dual deep equilibrium model providing fixed-point convergence as well as reduced memory requirements for training. We provide theoretical and empirical insights into the proposed models with numerical validation in a realistic 2D limited-view setting. The model-corrected learned primal-dual methods show excellent reconstruction quality with fast inference times and thus providing a methodological basis for real-time capable and scalable iterative reconstructions in photoacoustic tomography.

Unsupervised denoising for sparse multi-spectral computed tomography

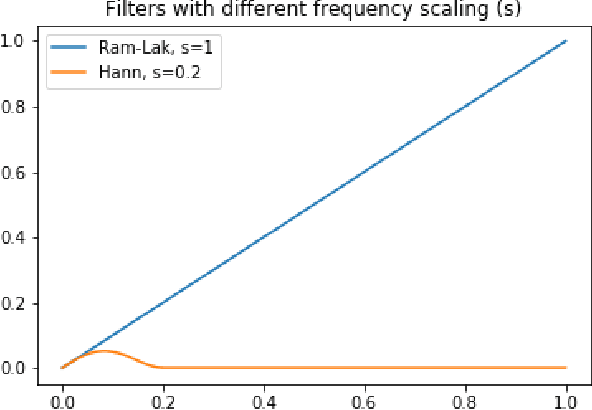
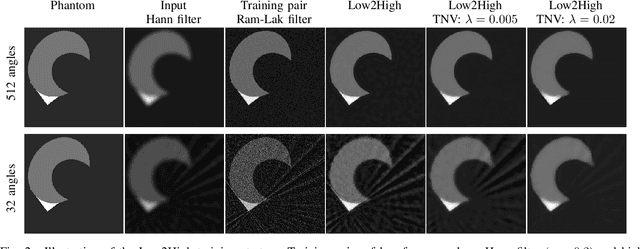
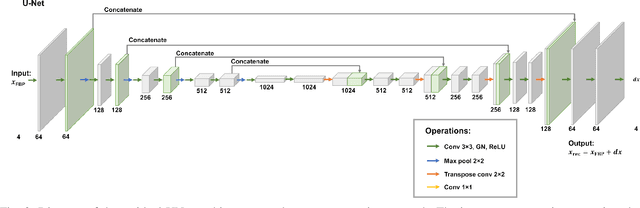
Multi-energy computed tomography (CT) with photon counting detectors (PCDs) enables spectral imaging as PCDs can assign the incoming photons to specific energy channels. However, PCDs with many spectral channels drastically increase the computational complexity of the CT reconstruction, and bespoke reconstruction algorithms need fine-tuning to varying noise statistics. \rev{Especially if many projections are taken, a large amount of data has to be collected and stored. Sparse view CT is one solution for data reduction. However, these issues are especially exacerbated when sparse imaging scenarios are encountered due to a significant reduction in photon counts.} In this work, we investigate the suitability of learning-based improvements to the challenging task of obtaining high-quality reconstructions from sparse measurements for a 64-channel PCD-CT. In particular, to overcome missing reference data for the training procedure, we propose an unsupervised denoising and artefact removal approach by exploiting different filter functions in the reconstruction and an explicit coupling of spectral channels with the nuclear norm. Performance is assessed on both simulated synthetic data and the openly available experimental Multi-Spectral Imaging via Computed Tomography (MUSIC) dataset. We compared the quality of our unsupervised method to iterative total nuclear variation regularized reconstructions and a supervised denoiser trained with reference data. We show that improved reconstruction quality can be achieved with flexibility on noise statistics and effective suppression of streaking artefacts when using unsupervised denoising with spectral coupling.

Reconstruction and segmentation from sparse sequential X-ray measurements of wood logs

In industrial applications it is common to scan objects on a moving conveyor belt. If slice-wise 2D computed tomography (CT) measurements of the moving object are obtained we call it a sequential scanning geometry. In this case, each slice on its own does not carry sufficient information to reconstruct a useful tomographic image. Thus, here we propose the use of a Dimension reduced Kalman Filter to accumulate information between slices and allow for sufficiently accurate reconstructions for further assessment of the object. Additionally, we propose to use an unsupervised clustering approach known as Density Peak Advanced, to perform a segmentation and spot density anomalies in the internal structure of the reconstructed objects. We evaluate the method in a proof of concept study for the application of wood log scanning for the industrial sawing process, where the goal is to spot anomalies within the wood log to allow for optimal sawing patterns. Reconstruction and segmentation quality is evaluated from experimental measurement data for various scenarios of severely undersampled X-measurements. Results show clearly that an improvement of reconstruction quality can be obtained by employing the Dimension reduced Kalman Filter allowing to robustly obtain the segmented logs.