A Primal-dual algorithm for image reconstruction with ICNNs

We address the optimization problem in a data-driven variational reconstruction framework, where the regularizer is parameterized by an input-convex neural network (ICNN). While gradient-based methods are commonly used to solve such problems, they struggle to effectively handle non-smoothness which often leads to slow convergence. Moreover, the nested structure of the neural network complicates the application of standard non-smooth optimization techniques, such as proximal algorithms. To overcome these challenges, we reformulate the problem and eliminate the network's nested structure. By relating this reformulation to epigraphical projections of the activation functions, we transform the problem into a convex optimization problem that can be efficiently solved using a primal-dual algorithm. We also prove that this reformulation is equivalent to the original variational problem. Through experiments on several imaging tasks, we demonstrate that the proposed approach outperforms subgradient methods in terms of both speed and stability.

Blessing of Dimensionality for Approximating Sobolev Classes on Manifolds

The manifold hypothesis says that natural high-dimensional data is actually supported on or around a low-dimensional manifold. Recent success of statistical and learning-based methods empirically supports this hypothesis, due to outperforming classical statistical intuition in very high dimensions. A natural step for analysis is thus to assume the manifold hypothesis and derive bounds that are independent of any embedding space. Theoretical implications in this direction have recently been explored in terms of generalization of ReLU networks and convergence of Langevin methods. We complement existing results by providing theoretical statistical complexity results, which directly relates to generalization properties. In particular, we demonstrate that the statistical complexity required to approximate a class of bounded Sobolev functions on a compact manifold is bounded from below, and moreover that this bound is dependent only on the intrinsic properties of the manifold. These provide complementary bounds for existing approximation results for ReLU networks on manifolds, which give upper bounds on generalization capacity.

Unsupervised Training of Convex Regularizers using Maximum Likelihood Estimation

Unsupervised learning is a training approach in the situation where ground truth data is unavailable, such as inverse imaging problems. We present an unsupervised Bayesian training approach to learning convex neural network regularizers using a fixed noisy dataset, based on a dual Markov chain estimation method. Compared to classical supervised adversarial regularization methods, where there is access to both clean images as well as unlimited to noisy copies, we demonstrate close performance on natural image Gaussian deconvolution and Poisson denoising tasks.

Weakly Convex Regularisers for Inverse Problems: Convergence of Critical Points and Primal-Dual Optimisation

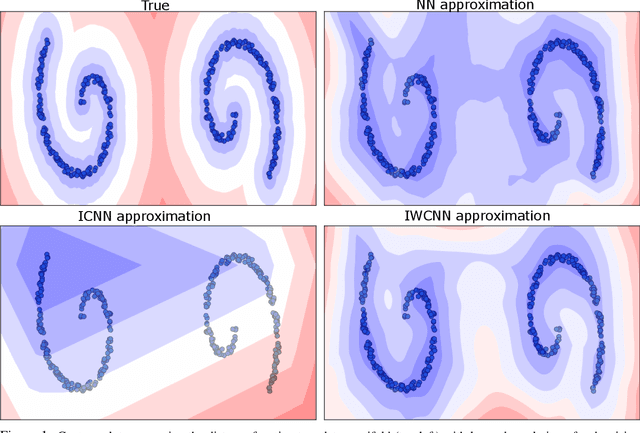
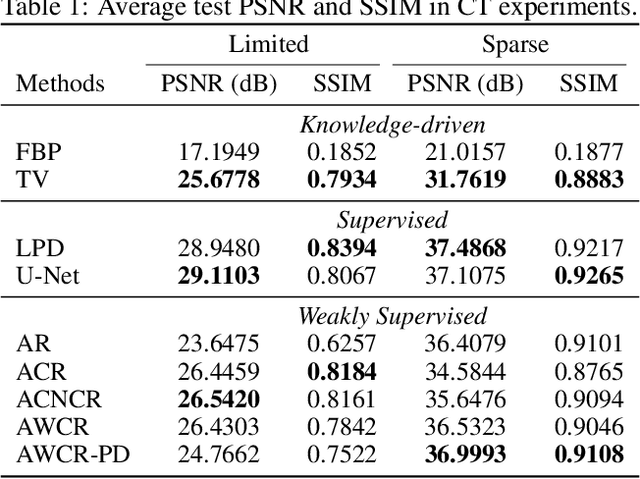
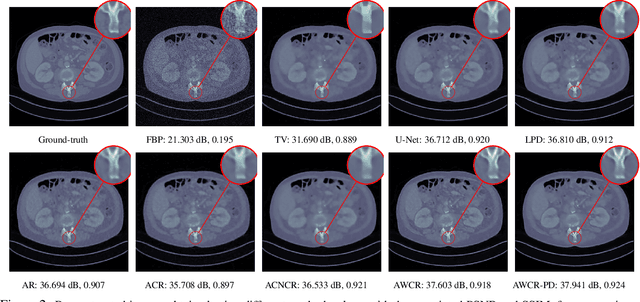
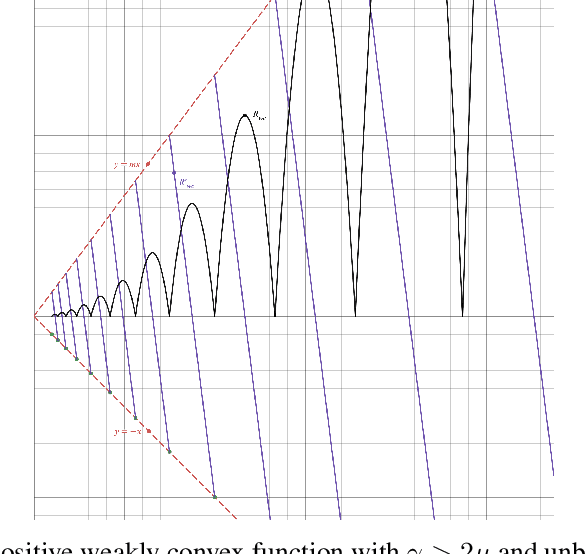
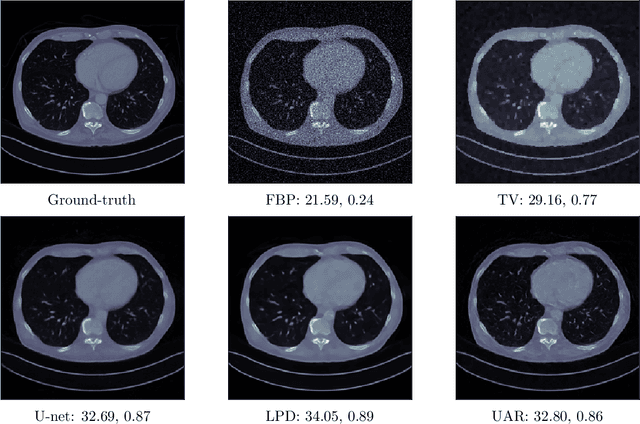
Variational regularisation is the primary method for solving inverse problems, and recently there has been considerable work leveraging deeply learned regularisation for enhanced performance. However, few results exist addressing the convergence of such regularisation, particularly within the context of critical points as opposed to global minima. In this paper, we present a generalised formulation of convergent regularisation in terms of critical points, and show that this is achieved by a class of weakly convex regularisers. We prove convergence of the primal-dual hybrid gradient method for the associated variational problem, and, given a Kurdyka-Lojasiewicz condition, an $\mathcal{O}(\log{k}/k)$ ergodic convergence rate. Finally, applying this theory to learned regularisation, we prove universal approximation for input weakly convex neural networks (IWCNN), and show empirically that IWCNNs can lead to improved performance of learned adversarial regularisers for computed tomography (CT) reconstruction.

Unsupervised approaches based on optimal transport and convex analysis for inverse problems in imaging

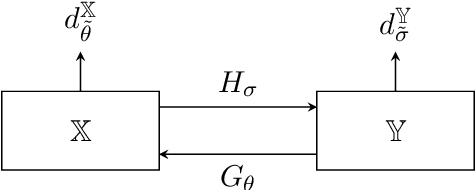
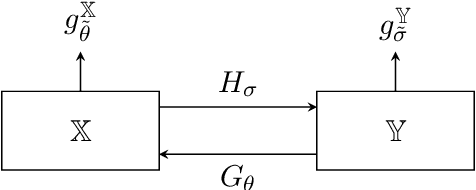
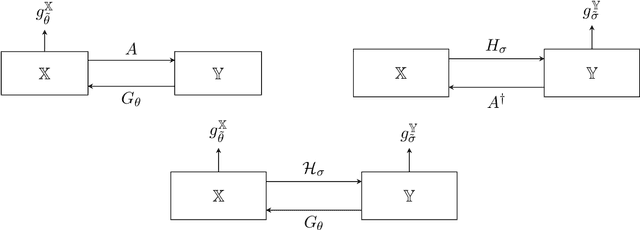
Unsupervised deep learning approaches have recently become one of the crucial research areas in imaging owing to their ability to learn expressive and powerful reconstruction operators even when paired high-quality training data is scarcely available. In this chapter, we review theoretically principled unsupervised learning schemes for solving imaging inverse problems, with a particular focus on methods rooted in optimal transport and convex analysis. We begin by reviewing the optimal transport-based unsupervised approaches such as the cycle-consistency-based models and learned adversarial regularization methods, which have clear probabilistic interpretations. Subsequently, we give an overview of a recent line of works on provably convergent learned optimization algorithms applied to accelerate the solution of imaging inverse problems, alongside their dedicated unsupervised training schemes. We also survey a number of provably convergent plug-and-play algorithms (based on gradient-step deep denoisers), which are among the most important and widely applied unsupervised approaches for imaging problems. At the end of this survey, we provide an overview of a few related unsupervised learning frameworks that complement our focused schemes. Together with a detailed survey, we provide an overview of the key mathematical results that underlie the methods reviewed in the chapter to keep our discussion self-contained.

Provably Convergent Data-Driven Convex-Nonconvex Regularization

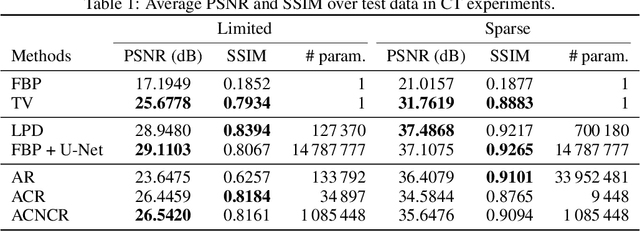
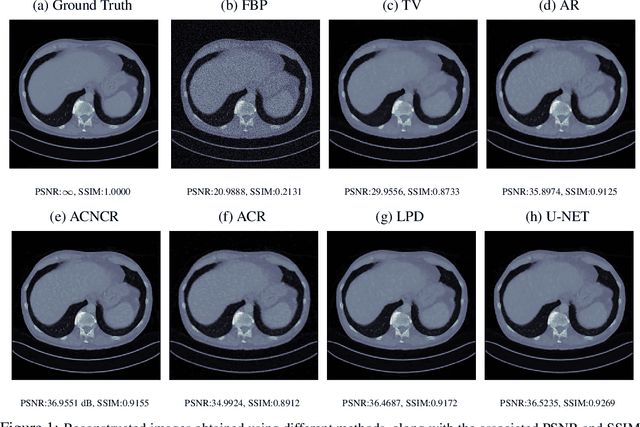
An emerging new paradigm for solving inverse problems is via the use of deep learning to learn a regularizer from data. This leads to high-quality results, but often at the cost of provable guarantees. In this work, we show how well-posedness and convergent regularization arises within the convex-nonconvex (CNC) framework for inverse problems. We introduce a novel input weakly convex neural network (IWCNN) construction to adapt the method of learned adversarial regularization to the CNC framework. Empirically we show that our method overcomes numerical issues of previous adversarial methods.

Dynamic Bilevel Learning with Inexact Line Search

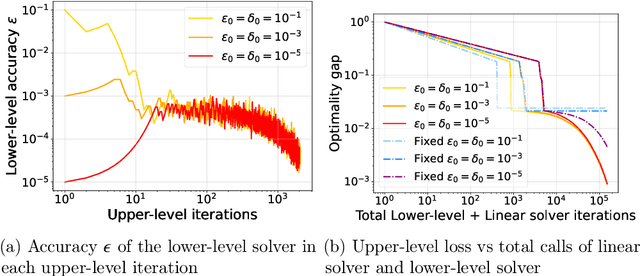
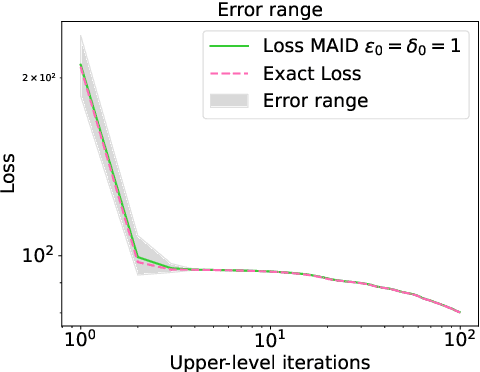
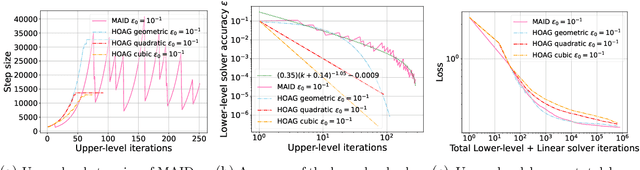
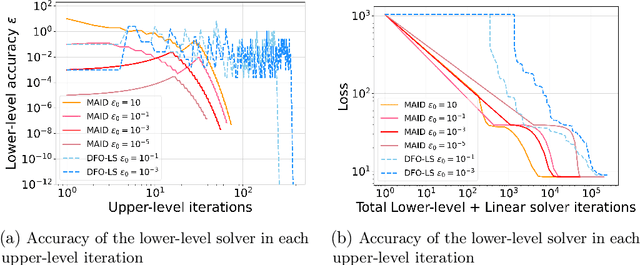
In various domains within imaging and data science, particularly when addressing tasks modeled utilizing the variational regularization approach, manually configuring regularization parameters presents a formidable challenge. The difficulty intensifies when employing regularizers involving a large number of hyperparameters. To overcome this challenge, bilevel learning is employed to learn suitable hyperparameters. However, due to the use of numerical solvers, the exact gradient with respect to the hyperparameters is unattainable, necessitating the use of methods relying on approximate gradients. State-of-the-art inexact methods a priori select a decreasing summable sequence of the required accuracy and only assure convergence given a sufficiently small fixed step size. Despite this, challenges persist in determining the Lipschitz constant of the hypergradient and identifying an appropriate fixed step size. Conversely, computing exact function values is not feasible, impeding the use of line search. In this work, we introduce a provably convergent inexact backtracking line search involving inexact function evaluations and hypergradients. We show convergence to a stationary point of the loss with respect to hyperparameters. Additionally, we propose an algorithm to determine the required accuracy dynamically. Our numerical experiments demonstrate the efficiency and feasibility of our approach for hyperparameter estimation in variational regularization problems, alongside its robustness in terms of the initial accuracy and step size choices.

Convergent regularization in inverse problems and linear plug-and-play denoisers

Plug-and-play (PnP) denoising is a popular iterative framework for solving imaging inverse problems using off-the-shelf image denoisers. Their empirical success has motivated a line of research that seeks to understand the convergence of PnP iterates under various assumptions on the denoiser. While a significant amount of research has gone into establishing the convergence of the PnP iteration for different regularity conditions on the denoisers, not much is known about the asymptotic properties of the converged solution as the noise level in the measurement tends to zero, i.e., whether PnP methods are provably convergent regularization schemes under reasonable assumptions on the denoiser. This paper serves two purposes: first, we provide an overview of the classical regularization theory in inverse problems and survey a few notable recent data-driven methods that are provably convergent regularization schemes. We then continue to discuss PnP algorithms and their established convergence guarantees. Subsequently, we consider PnP algorithms with linear denoisers and propose a novel spectral filtering technique to control the strength of regularization arising from the denoiser. Further, by relating the implicit regularization of the denoiser to an explicit regularization functional, we rigorously show that PnP with linear denoisers leads to a convergent regularization scheme. More specifically, we prove that in the limit as the noise vanishes, the PnP reconstruction converges to the minimizer of a regularization potential subject to the solution satisfying the noiseless operator equation. The theoretical analysis is corroborated by numerical experiments for the classical inverse problem of tomographic image reconstruction.

NF-ULA: Langevin Monte Carlo with Normalizing Flow Prior for Imaging Inverse Problems

Bayesian methods for solving inverse problems are a powerful alternative to classical methods since the Bayesian approach gives a probabilistic description of the problems and offers the ability to quantify the uncertainty in the solution. Meanwhile, solving inverse problems by data-driven techniques also proves to be successful, due to the increasing representation ability of data-based models. In this work, we try to incorporate the data-based models into a class of Langevin-based sampling algorithms in Bayesian inference. Loosely speaking, we introduce NF-ULA (Unadjusted Langevin algorithms by Normalizing Flows), which involves learning a normalizing flow as the prior. In particular, our algorithm only requires a pre-trained normalizing flow, which is independent of the considered inverse problem and the forward operator. We perform theoretical analysis by investigating the well-posedness of the Bayesian solution and the non-asymptotic convergence of the NF-ULA algorithm. The efficacy of the proposed NF-ULA algorithm is demonstrated in various imaging problems, including image deblurring, image inpainting, and limited-angle X-ray computed tomography (CT) reconstruction.

Fluctuation-based deconvolution in fluorescence microscopy using plug-and-play denoisers

The spatial resolution of images of living samples obtained by fluorescence microscopes is physically limited due to the diffraction of visible light, which makes the study of entities of size less than the diffraction barrier (around 200 nm in the x-y plane) very challenging. To overcome this limitation, several deconvolution and super-resolution techniques have been proposed. Within the framework of inverse problems, modern approaches in fluorescence microscopy reconstruct a super-resolved image from a temporal stack of frames by carefully designing suitable hand-crafted sparsity-promoting regularisers. Numerically, such approaches are solved by proximal gradient-based iterative schemes. Aiming at obtaining a reconstruction more adapted to sample geometries (e.g. thin filaments), we adopt a plug-and-play denoising approach with convergence guarantees and replace the proximity operator associated with the explicit image regulariser with an image denoiser (i.e. a pre-trained network) which, upon appropriate training, mimics the action of an implicit prior. To account for the independence of the fluctuations between molecules, the model relies on second-order statistics. The denoiser is then trained on covariance images coming from data representing sequences of fluctuating fluorescent molecules with filament structure. The method is evaluated on both simulated and real fluorescence microscopy images, showing its ability to correctly reconstruct filament structures with high values of peak signal-to-noise ratio (PSNR).