Dynamic Bilevel Learning with Inexact Line Search
Paper and Code
Aug 19, 2023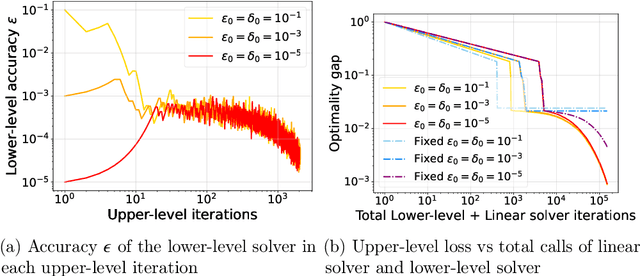
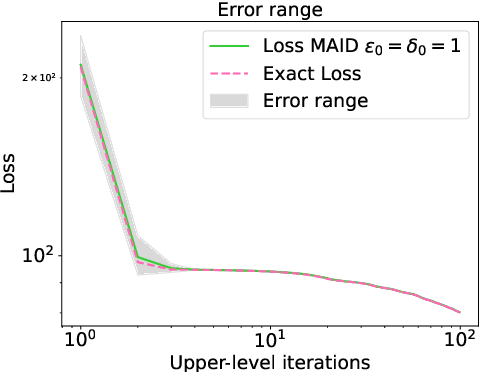
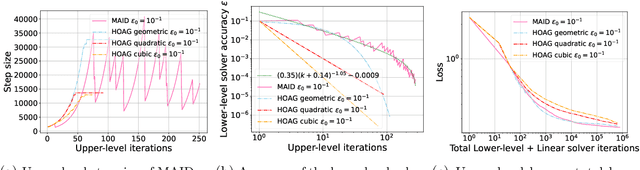
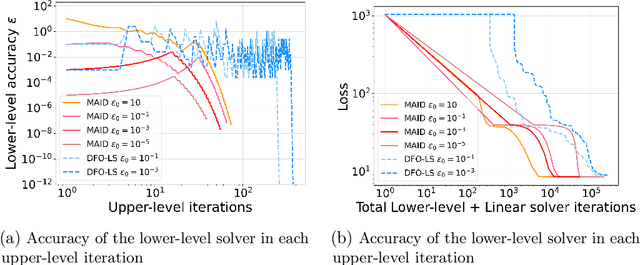
In various domains within imaging and data science, particularly when addressing tasks modeled utilizing the variational regularization approach, manually configuring regularization parameters presents a formidable challenge. The difficulty intensifies when employing regularizers involving a large number of hyperparameters. To overcome this challenge, bilevel learning is employed to learn suitable hyperparameters. However, due to the use of numerical solvers, the exact gradient with respect to the hyperparameters is unattainable, necessitating the use of methods relying on approximate gradients. State-of-the-art inexact methods a priori select a decreasing summable sequence of the required accuracy and only assure convergence given a sufficiently small fixed step size. Despite this, challenges persist in determining the Lipschitz constant of the hypergradient and identifying an appropriate fixed step size. Conversely, computing exact function values is not feasible, impeding the use of line search. In this work, we introduce a provably convergent inexact backtracking line search involving inexact function evaluations and hypergradients. We show convergence to a stationary point of the loss with respect to hyperparameters. Additionally, we propose an algorithm to determine the required accuracy dynamically. Our numerical experiments demonstrate the efficiency and feasibility of our approach for hyperparameter estimation in variational regularization problems, alongside its robustness in terms of the initial accuracy and step size choices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge