Unsupervised Training of Convex Regularizers using Maximum Likelihood Estimation

Unsupervised learning is a training approach in the situation where ground truth data is unavailable, such as inverse imaging problems. We present an unsupervised Bayesian training approach to learning convex neural network regularizers using a fixed noisy dataset, based on a dual Markov chain estimation method. Compared to classical supervised adversarial regularization methods, where there is access to both clean images as well as unlimited to noisy copies, we demonstrate close performance on natural image Gaussian deconvolution and Poisson denoising tasks.

NF-ULA: Langevin Monte Carlo with Normalizing Flow Prior for Imaging Inverse Problems

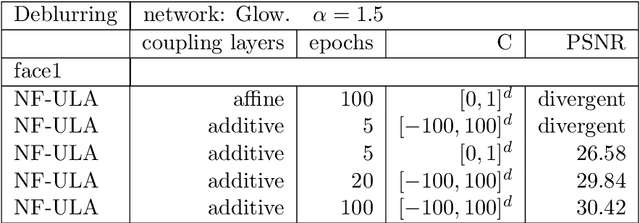
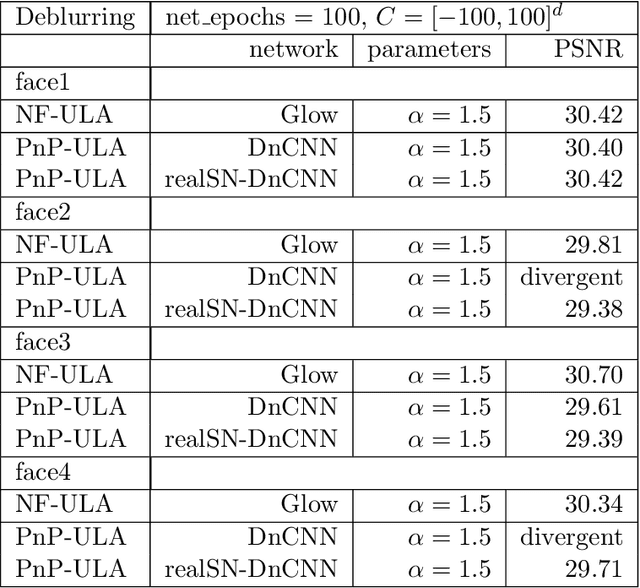
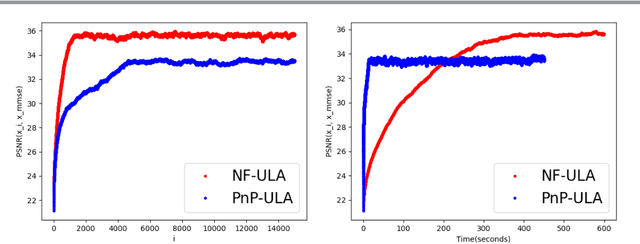
Bayesian methods for solving inverse problems are a powerful alternative to classical methods since the Bayesian approach gives a probabilistic description of the problems and offers the ability to quantify the uncertainty in the solution. Meanwhile, solving inverse problems by data-driven techniques also proves to be successful, due to the increasing representation ability of data-based models. In this work, we try to incorporate the data-based models into a class of Langevin-based sampling algorithms in Bayesian inference. Loosely speaking, we introduce NF-ULA (Unadjusted Langevin algorithms by Normalizing Flows), which involves learning a normalizing flow as the prior. In particular, our algorithm only requires a pre-trained normalizing flow, which is independent of the considered inverse problem and the forward operator. We perform theoretical analysis by investigating the well-posedness of the Bayesian solution and the non-asymptotic convergence of the NF-ULA algorithm. The efficacy of the proposed NF-ULA algorithm is demonstrated in various imaging problems, including image deblurring, image inpainting, and limited-angle X-ray computed tomography (CT) reconstruction.