Un-evaluated Solutions May Be Valuable in Expensive Optimization

Expensive optimization problems (EOPs) are prevalent in real-world applications, where the evaluation of a single solution requires a significant amount of resources. In our study of surrogate-assisted evolutionary algorithms (SAEAs) in EOPs, we discovered an intriguing phenomenon. Because only a limited number of solutions are evaluated in each iteration, relying solely on these evaluated solutions for evolution can lead to reduced disparity in successive populations. This, in turn, hampers the reproduction operators' ability to generate superior solutions, thereby reducing the algorithm's convergence speed. To address this issue, we propose a strategic approach that incorporates high-quality, un-evaluated solutions predicted by surrogate models during the selection phase. This approach aims to improve the distribution of evaluated solutions, thereby generating a superior next generation of solutions. This work details specific implementations of this concept across various reproduction operators and validates its effectiveness using multiple surrogate models. Experimental results demonstrate that the proposed strategy significantly enhances the performance of surrogate-assisted evolutionary algorithms. Compared to mainstream SAEAs and Bayesian optimization algorithms, our approach incorporating the un-evaluated solution strategy shows a marked improvement.

Bi-modality Images Transfer with a Discrete Process Matching Method

Recently, medical image synthesis gains more and more popularity, along with the rapid development of generative models. Medical image synthesis aims to generate an unacquired image modality, often from other observed data modalities. Synthesized images can be used for clinical diagnostic assistance, data augmentation for model training and validation or image quality improving. In the meanwhile, the flow-based models are among the successful generative models for the ability of generating realistic and high-quality synthetic images. However, most flow-based models require to calculate flow ordinary different equation (ODE) evolution steps in transfer process, for which the performances are significantly limited by heavy computation time due to a large number of time iterations. In this paper, we propose a novel flow-based model, namely Discrete Process Matching (DPM) to accomplish the bi-modality image transfer tasks. Different to other flow matching based models, we propose to utilize both forward and backward ODE flow and enhance the consistency on the intermediate images of few discrete time steps, resulting in a transfer process with much less iteration steps while maintaining high-quality generations for both modalities. Our experiments on three datasets of MRI T1/T2 and CT/MRI demonstrate that DPM outperforms other state-of-the-art flow-based methods for bi-modality image synthesis, achieving higher image quality with less computation time cost.

Few-shot Multi-Task Learning of Linear Invariant Features with Meta Subspace Pursuit

Data scarcity poses a serious threat to modern machine learning and artificial intelligence, as their practical success typically relies on the availability of big datasets. One effective strategy to mitigate the issue of insufficient data is to first harness information from other data sources possessing certain similarities in the study design stage, and then employ the multi-task or meta learning framework in the analysis stage. In this paper, we focus on multi-task (or multi-source) linear models whose coefficients across tasks share an invariant low-rank component, a popular structural assumption considered in the recent multi-task or meta learning literature. Under this assumption, we propose a new algorithm, called Meta Subspace Pursuit (abbreviated as Meta-SP), that provably learns this invariant subspace shared by different tasks. Under this stylized setup for multi-task or meta learning, we establish both the algorithmic and statistical guarantees of the proposed method. Extensive numerical experiments are conducted, comparing Meta-SP against several competing methods, including popular, off-the-shelf model-agnostic meta learning algorithms such as ANIL. These experiments demonstrate that Meta-SP achieves superior performance over the competing methods in various aspects.

Large Language Models as Surrogate Models in Evolutionary Algorithms: A Preliminary Study

Large Language Models (LLMs) have achieved significant progress across various fields and have exhibited strong potential in evolutionary computation, such as generating new solutions and automating algorithm design. Surrogate-assisted selection is a core step in evolutionary algorithms to solve expensive optimization problems by reducing the number of real evaluations. Traditionally, this has relied on conventional machine learning methods, leveraging historical evaluated evaluations to predict the performance of new solutions. In this work, we propose a novel surrogate model based purely on LLM inference capabilities, eliminating the need for training. Specifically, we formulate model-assisted selection as a classification and regression problem, utilizing LLMs to directly evaluate the quality of new solutions based on historical data. This involves predicting whether a solution is good or bad, or approximating its value. This approach is then integrated into evolutionary algorithms, termed LLM-assisted EA (LAEA). Detailed experiments compared the visualization results of 2D data from 9 mainstream LLMs, as well as their performance on optimization problems. The experimental results demonstrate that LLMs have significant potential as surrogate models in evolutionary computation, achieving performance comparable to traditional surrogate models only using inference. This work offers new insights into the application of LLMs in evolutionary computation. Code is available at: https://github.com/hhyqhh/LAEA.git

A First Look at Kolmogorov-Arnold Networks in Surrogate-assisted Evolutionary Algorithms

Surrogate-assisted Evolutionary Algorithm (SAEA) is an essential method for solving expensive expensive problems. Utilizing surrogate models to substitute the optimization function can significantly reduce reliance on the function evaluations during the search process, thereby lowering the optimization costs. The construction of surrogate models is a critical component in SAEAs, with numerous machine learning algorithms playing a pivotal role in the model-building phase. This paper introduces Kolmogorov-Arnold Networks (KANs) as surrogate models within SAEAs, examining their application and effectiveness. We employ KANs for regression and classification tasks, focusing on the selection of promising solutions during the search process, which consequently reduces the number of expensive function evaluations. Experimental results indicate that KANs demonstrate commendable performance within SAEAs, effectively decreasing the number of function calls and enhancing the optimization efficiency. The relevant code is publicly accessible and can be found in the GitHub repository.

Model Uncertainty in Evolutionary Optimization and Bayesian Optimization: A Comparative Analysis

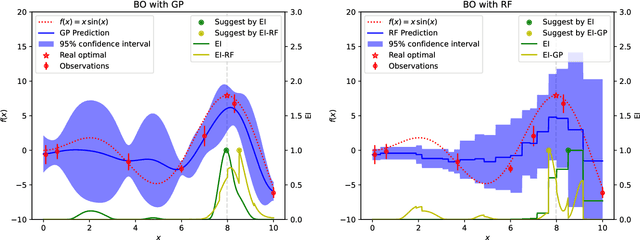
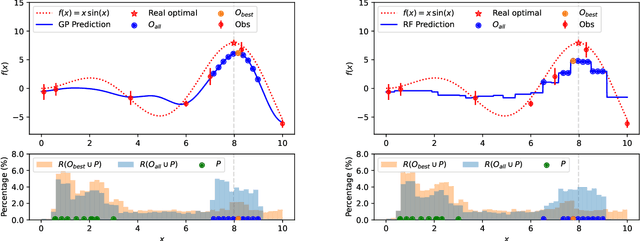
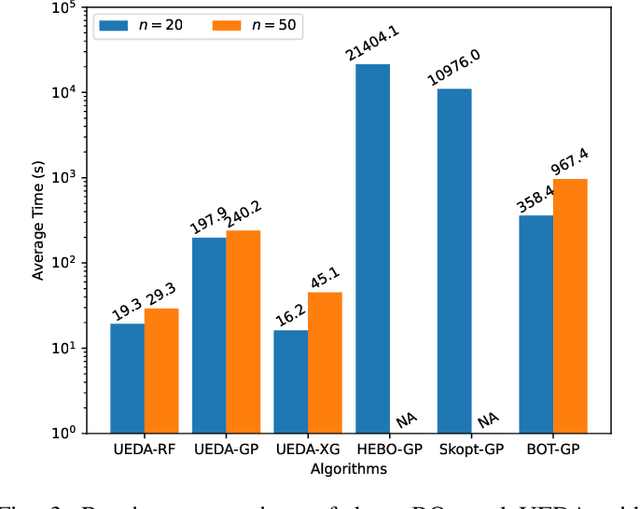
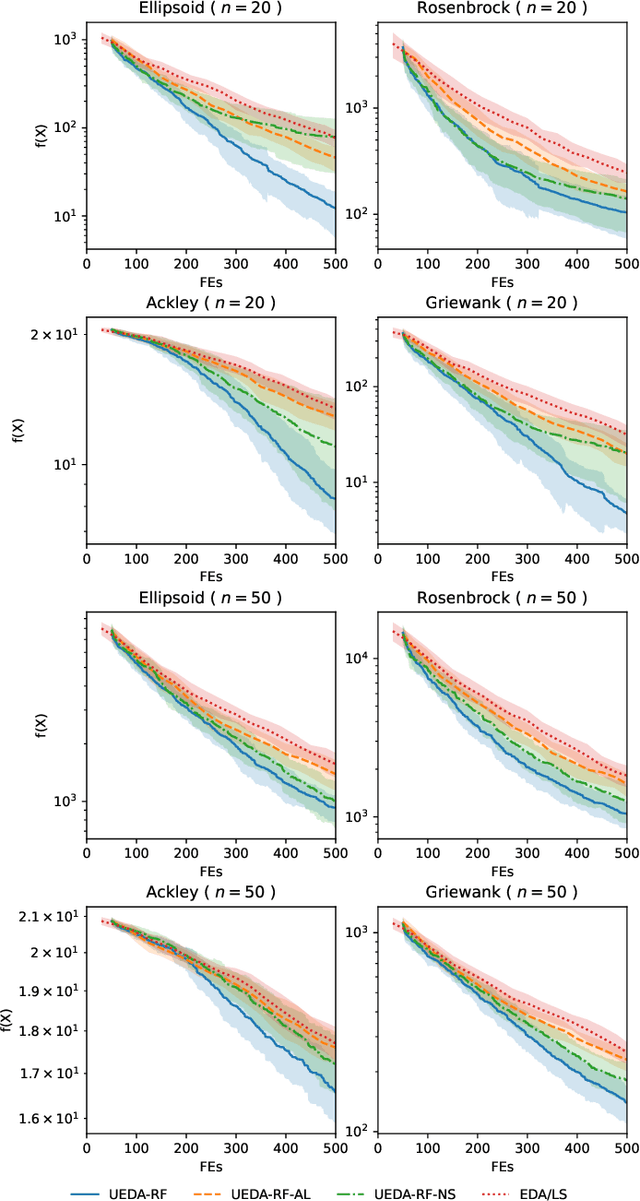
Black-box optimization problems, which are common in many real-world applications, require optimization through input-output interactions without access to internal workings. This often leads to significant computational resources being consumed for simulations. Bayesian Optimization (BO) and Surrogate-Assisted Evolutionary Algorithm (SAEA) are two widely used gradient-free optimization techniques employed to address such challenges. Both approaches follow a similar iterative procedure that relies on surrogate models to guide the search process. This paper aims to elucidate the similarities and differences in the utilization of model uncertainty between these two methods, as well as the impact of model inaccuracies on algorithmic performance. A novel model-assisted strategy is introduced, which utilizes unevaluated solutions to generate offspring, leveraging the population-based search capabilities of evolutionary algorithm to enhance the effectiveness of model-assisted optimization. Experimental results demonstrate that the proposed approach outperforms mainstream Bayesian optimization algorithms in terms of accuracy and efficiency.

Enhancing SAEAs with Unevaluated Solutions: A Case Study of Relation Model for Expensive Optimization

Surrogate-assisted evolutionary algorithms (SAEAs) hold significant importance in resolving expensive optimization problems~(EOPs). Extensive efforts have been devoted to improving the efficacy of SAEAs through the development of proficient model-assisted selection methods. However, generating high-quality solutions is a prerequisite for selection. The fundamental paradigm of evaluating a limited number of solutions in each generation within SAEAs reduces the variance of adjacent populations, thus impacting the quality of offspring solutions. This is a frequently encountered issue, yet it has not gained widespread attention. This paper presents a framework using unevaluated solutions to enhance the efficiency of SAEAs. The surrogate model is employed to identify high-quality solutions for direct generation of new solutions without evaluation. To ensure dependable selection, we have introduced two tailored relation models for the selection of the optimal solution and the unevaluated population. A comprehensive experimental analysis is performed on two test suites, which showcases the superiority of the relation model over regression and classification models in the selection phase. Furthermore, the surrogate-selected unevaluated solutions with high potential have been shown to significantly enhance the efficiency of the algorithm.

SyMOT-Flow: Learning optimal transport flow for two arbitrary distributions with maximum mean discrepancy

Finding a transformation between two unknown probability distributions from samples is crucial for modeling complex data distributions and perform tasks such as density estimation, sample generation, and statistical inference. One powerful framework for such transformations is normalizing flow, which transforms an unknown distribution into a standard normal distribution using an invertible network. In this paper, we introduce a novel model called SyMOT-Flow that trains an invertible transformation by minimizing the symmetric maximum mean discrepancy between samples from two unknown distributions, and we incorporate an optimal transport cost as regularization to obtain a short-distance and interpretable transformation. The resulted transformation leads to more stable and accurate sample generation. We establish several theoretical results for the proposed model and demonstrate its effectiveness with low-dimensional illustrative examples as well as high-dimensional generative samples obtained through the forward and reverse flows.

NF-ULA: Langevin Monte Carlo with Normalizing Flow Prior for Imaging Inverse Problems

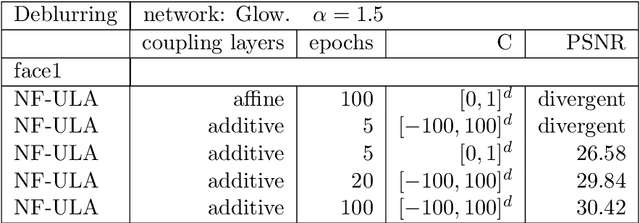
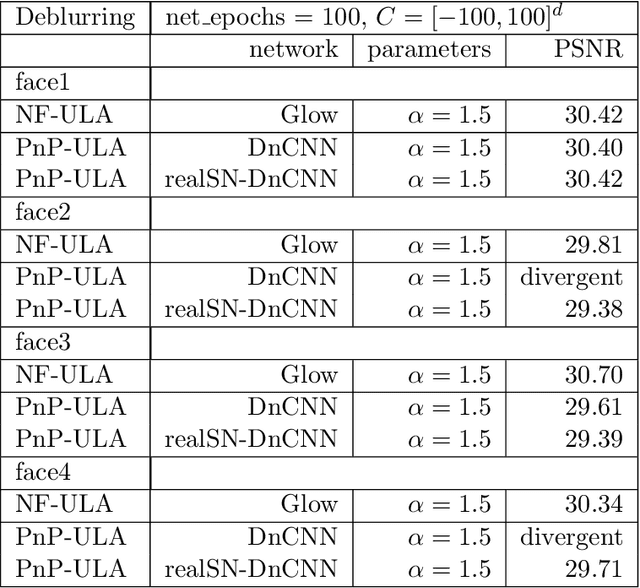
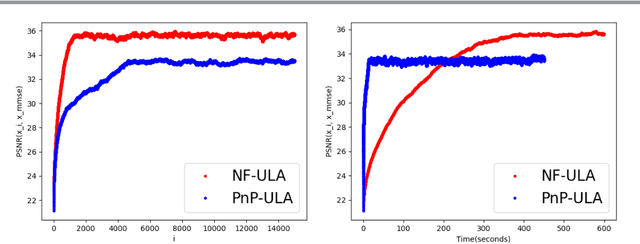
Bayesian methods for solving inverse problems are a powerful alternative to classical methods since the Bayesian approach gives a probabilistic description of the problems and offers the ability to quantify the uncertainty in the solution. Meanwhile, solving inverse problems by data-driven techniques also proves to be successful, due to the increasing representation ability of data-based models. In this work, we try to incorporate the data-based models into a class of Langevin-based sampling algorithms in Bayesian inference. Loosely speaking, we introduce NF-ULA (Unadjusted Langevin algorithms by Normalizing Flows), which involves learning a normalizing flow as the prior. In particular, our algorithm only requires a pre-trained normalizing flow, which is independent of the considered inverse problem and the forward operator. We perform theoretical analysis by investigating the well-posedness of the Bayesian solution and the non-asymptotic convergence of the NF-ULA algorithm. The efficacy of the proposed NF-ULA algorithm is demonstrated in various imaging problems, including image deblurring, image inpainting, and limited-angle X-ray computed tomography (CT) reconstruction.

Dataset-free Deep learning Method for Low-Dose CT Image Reconstruction

Low-dose CT (LDCT) imaging attracted a considerable interest for the reduction of the object's exposure to X-ray radiation. In recent years, supervised deep learning has been extensively studied for LDCT image reconstruction, which trains a network over a dataset containing many pairs of normal-dose and low-dose images. However, the challenge on collecting many such pairs in the clinical setup limits the application of such supervised-learning-based methods for LDCT image reconstruction in practice. Aiming at addressing the challenges raised by the collection of training dataset, this paper proposed a unsupervised deep learning method for LDCT image reconstruction, which does not require any external training data. The proposed method is built on a re-parametrization technique for Bayesian inference via deep network with random weights, combined with additional total variational (TV) regularization. The experiments show that the proposed method noticeably outperforms existing dataset-free image reconstruction methods on the test data.