It's Morphing Time: Unleashing the Potential of Multiple LLMs via Multi-objective Optimization

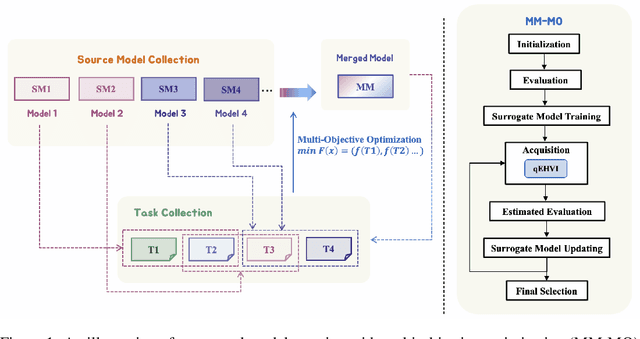
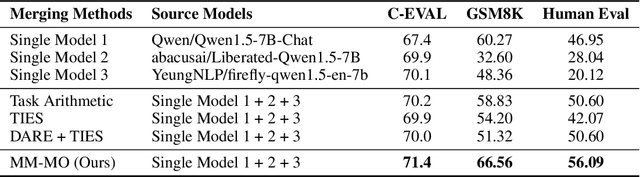
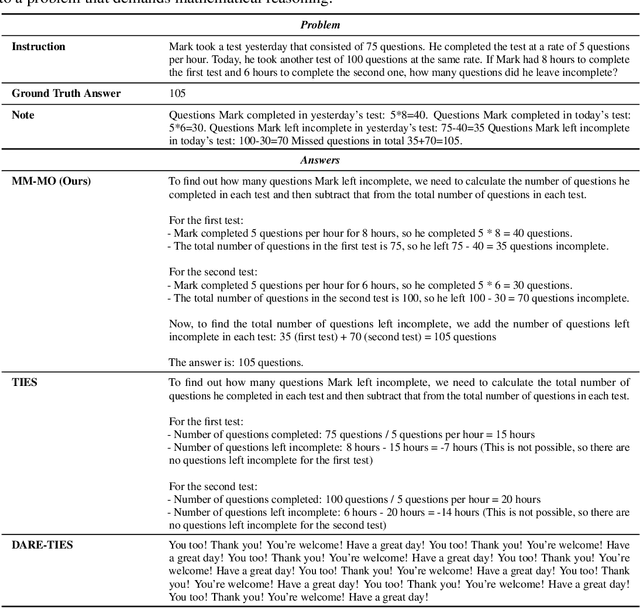
In this paper, we introduce a novel approach for large language model merging via black-box multi-objective optimization algorithms. The goal of model merging is to combine multiple models, each excelling in different tasks, into a single model that outperforms any of the individual source models. However, model merging faces two significant challenges: First, existing methods rely heavily on human intuition and customized strategies. Second, parameter conflicts often arise during merging, and while methods like DARE [1] can alleviate this issue, they tend to stochastically drop parameters, risking the loss of important delta parameters. To address these challenges, we propose the MM-MO method, which automates the search for optimal merging configurations using multi-objective optimization algorithms, eliminating the need for human intuition. During the configuration searching process, we use estimated performance across multiple diverse tasks as optimization objectives in order to alleviate the parameter conflicting between different source models without losing crucial delta parameters. We conducted comparative experiments with other mainstream model merging methods, demonstrating that our method consistently outperforms them. Moreover, our experiments reveal that even task types not explicitly targeted as optimization objectives show performance improvements, indicating that our method enhances the overall potential of the model rather than merely overfitting to specific task types. This approach provides a significant advancement in model merging techniques, offering a robust and plug-and-play solution for integrating diverse models into a unified, high-performing model.

A First Look at Kolmogorov-Arnold Networks in Surrogate-assisted Evolutionary Algorithms

Surrogate-assisted Evolutionary Algorithm (SAEA) is an essential method for solving expensive expensive problems. Utilizing surrogate models to substitute the optimization function can significantly reduce reliance on the function evaluations during the search process, thereby lowering the optimization costs. The construction of surrogate models is a critical component in SAEAs, with numerous machine learning algorithms playing a pivotal role in the model-building phase. This paper introduces Kolmogorov-Arnold Networks (KANs) as surrogate models within SAEAs, examining their application and effectiveness. We employ KANs for regression and classification tasks, focusing on the selection of promising solutions during the search process, which consequently reduces the number of expensive function evaluations. Experimental results indicate that KANs demonstrate commendable performance within SAEAs, effectively decreasing the number of function calls and enhancing the optimization efficiency. The relevant code is publicly accessible and can be found in the GitHub repository.

Expensive Multi-Objective Bayesian Optimization Based on Diffusion Models

Multi-objective Bayesian optimization (MOBO) has shown promising performance on various expensive multi-objective optimization problems (EMOPs). However, effectively modeling complex distributions of the Pareto optimal solutions is difficult with limited function evaluations. Existing Pareto set learning algorithms may exhibit considerable instability in such expensive scenarios, leading to significant deviations between the obtained solution set and the Pareto set (PS). In this paper, we propose a novel Composite Diffusion Model based Pareto Set Learning algorithm, namely CDM-PSL, for expensive MOBO. CDM-PSL includes both unconditional and conditional diffusion model for generating high-quality samples. Besides, we introduce an information entropy based weighting method to balance different objectives of EMOPs. This method is integrated with the guiding strategy, ensuring that all the objectives are appropriately balanced and given due consideration during the optimization process; Extensive experimental results on both synthetic benchmarks and real-world problems demonstrates that our proposed algorithm attains superior performance compared with various state-of-the-art MOBO algorithms.

Towards Geometry-Aware Pareto Set Learning for Neural Multi-Objective Combinatorial Optimization

Multi-objective combinatorial optimization (MOCO) problems are prevalent in various real-world applications. Most existing neural methods for MOCO problems rely solely on decomposition and utilize precise hypervolume to enhance diversity. However, these methods often approximate only limited regions of the Pareto front and spend excessive time on diversity enhancement because of ambiguous decomposition and time-consuming hypervolume calculation. To address these limitations, we design a Geometry-Aware Pareto set Learning algorithm named GAPL, which provides a novel geometric perspective for neural MOCO via a Pareto attention model based on hypervolume expectation maximization. In addition, we propose a hypervolume residual update strategy to enable the Pareto attention model to capture both local and non-local information of the Pareto set/front. We also design a novel inference approach to further improve quality of the solution set and speed up hypervolume calculation and local subset selection. Experimental results on three classic MOCO problems demonstrate that our GAPL outperforms state-of-the-art neural baselines via superior decomposition and efficient diversity enhancement.

Pointer Networks Trained Better via Evolutionary Algorithms

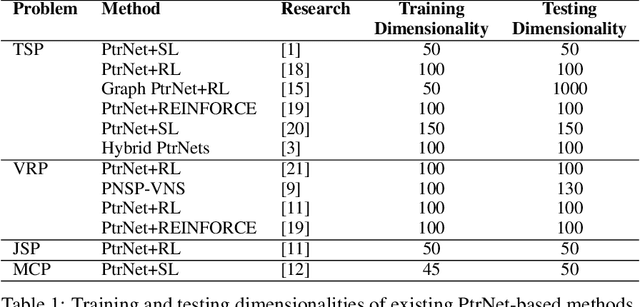
Pointer Network (PtrNet) is a specific neural network for solving Combinatorial Optimization Problems (COPs). While PtrNets offer real-time feed-forward inference for complex COPs instances, its quality of the results tends to be less satisfactory. One possible reason is that such issue suffers from the lack of global search ability of the gradient descent, which is frequently employed in traditional PtrNet training methods including both supervised learning and reinforcement learning. To improve the performance of PtrNet, this paper delves deeply into the advantages of training PtrNet with Evolutionary Algorithms (EAs), which have been widely acknowledged for not easily getting trapped by local optima. Extensive empirical studies based on the Travelling Salesman Problem (TSP) have been conducted. Results demonstrate that PtrNet trained with EA can consistently perform much better inference results than eight state-of-the-art methods on various problem scales. Compared with gradient descent based PtrNet training methods, EA achieves up to 30.21\% improvement in quality of the solution with the same computational time. With this advantage, this paper is able to at the first time report the results of solving 1000-dimensional TSPs by training a PtrNet on the same dimensionality, which strongly suggests that scaling up the training instances is in need to improve the performance of PtrNet on solving higher-dimensional COPs.