Towards Universal Offline Black-Box Optimization via Learning Language Model Embeddings

The pursuit of universal black-box optimization (BBO) algorithms is a longstanding goal. However, unlike domains such as language or vision, where scaling structured data has driven generalization, progress in offline BBO remains hindered by the lack of unified representations for heterogeneous numerical spaces. Thus, existing offline BBO approaches are constrained to single-task and fixed-dimensional settings, failing to achieve cross-domain universal optimization. Recent advances in language models (LMs) offer a promising path forward: their embeddings capture latent relationships in a unifying way, enabling universal optimization across different data types possible. In this paper, we discuss multiple potential approaches, including an end-to-end learning framework in the form of next-token prediction, as well as prioritizing the learning of latent spaces with strong representational capabilities. To validate the effectiveness of these methods, we collect offline BBO tasks and data from open-source academic works for training. Experiments demonstrate the universality and effectiveness of our proposed methods. Our findings suggest that unifying language model priors and learning string embedding space can overcome traditional barriers in universal BBO, paving the way for general-purpose BBO algorithms. The code is provided at https://github.com/lamda-bbo/universal-offline-bbo.

Quality-Diversity Red-Teaming: Automated Generation of High-Quality and Diverse Attackers for Large Language Models

Ensuring safety of large language models (LLMs) is important. Red teaming--a systematic approach to identifying adversarial prompts that elicit harmful responses from target LLMs--has emerged as a crucial safety evaluation method. Within this framework, the diversity of adversarial prompts is essential for comprehensive safety assessments. We find that previous approaches to red-teaming may suffer from two key limitations. First, they often pursue diversity through simplistic metrics like word frequency or sentence embedding similarity, which may not capture meaningful variation in attack strategies. Second, the common practice of training a single attacker model restricts coverage across potential attack styles and risk categories. This paper introduces Quality-Diversity Red-Teaming (QDRT), a new framework designed to address these limitations. QDRT achieves goal-driven diversity through behavior-conditioned training and implements a behavioral replay buffer in an open-ended manner. Additionally, it trains multiple specialized attackers capable of generating high-quality attacks across diverse styles and risk categories. Our empirical evaluation demonstrates that QDRT generates attacks that are both more diverse and more effective against a wide range of target LLMs, including GPT-2, Llama-3, Gemma-2, and Qwen2.5. This work advances the field of LLM safety by providing a systematic and effective approach to automated red-teaming, ultimately supporting the responsible deployment of LLMs.

Runtime Analysis of Evolutionary NAS for Multiclass Classification

Evolutionary neural architecture search (ENAS) is a key part of evolutionary machine learning, which commonly utilizes evolutionary algorithms (EAs) to automatically design high-performing deep neural architectures. During past years, various ENAS methods have been proposed with exceptional performance. However, the theory research of ENAS is still in the infant. In this work, we step for the runtime analysis, which is an essential theory aspect of EAs, of ENAS upon multiclass classification problems. Specifically, we first propose a benchmark to lay the groundwork for the analysis. Furthermore, we design a two-level search space, making it suitable for multiclass classification problems and consistent with the common settings of ENAS. Based on both designs, we consider (1+1)-ENAS algorithms with one-bit and bit-wise mutations, and analyze their upper and lower bounds on the expected runtime. We prove that the algorithm using both mutations can find the optimum with the expected runtime upper bound of $O(rM\ln{rM})$ and lower bound of $\Omega(rM\ln{M})$. This suggests that a simple one-bit mutation may be greatly considered, given that most state-of-the-art ENAS methods are laboriously designed with the bit-wise mutation. Empirical studies also support our theoretical proof.

Automating Versatile Time-Series Analysis with Tiny Transformers on Embedded FPGAs

Transformer-based models have shown strong performance across diverse time-series tasks, but their deployment on resource-constrained devices remains challenging due to high memory and computational demand. While prior work targeting Microcontroller Units (MCUs) has explored hardware-specific optimizations, such approaches are often task-specific and limited to 8-bit fixed-point precision. Field-Programmable Gate Arrays (FPGAs) offer greater flexibility, enabling fine-grained control over data precision and architecture. However, existing FPGA-based deployments of Transformers for time-series analysis typically focus on high-density platforms with manual configuration. This paper presents a unified and fully automated deployment framework for Tiny Transformers on embedded FPGAs. Our framework supports a compact encoder-only Transformer architecture across three representative time-series tasks (forecasting, classification, and anomaly detection). It combines quantization-aware training (down to 4 bits), hardware-aware hyperparameter search using Optuna, and automatic VHDL generation for seamless deployment. We evaluate our framework on six public datasets across two embedded FPGA platforms. Results show that our framework produces integer-only, task-specific Transformer accelerators achieving as low as 0.033 mJ per inference with millisecond latency on AMD Spartan-7, while also providing insights into deployment feasibility on Lattice iCE40. All source code will be released in the GitHub repository (https://github.com/Edwina1030/TinyTransformer4TS).

Open3DBench: Open-Source Benchmark for 3D-IC Backend Implementation and PPA Evaluation

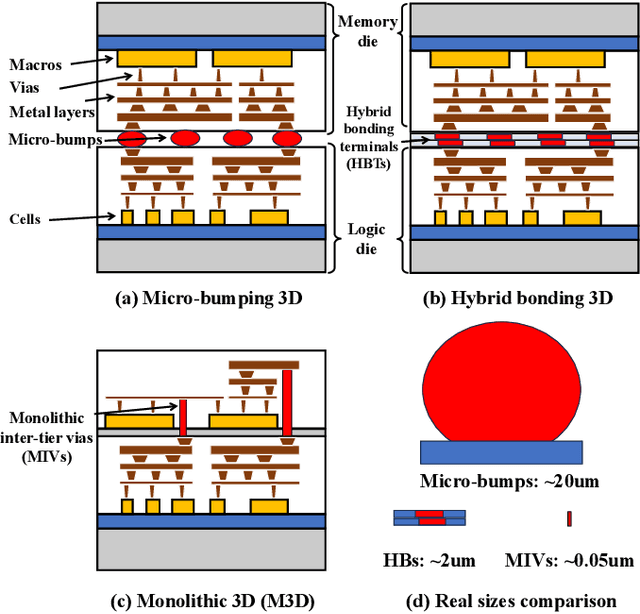
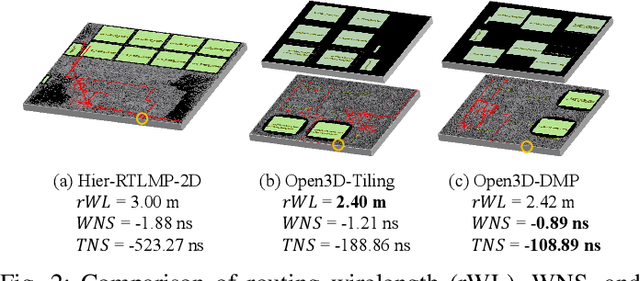
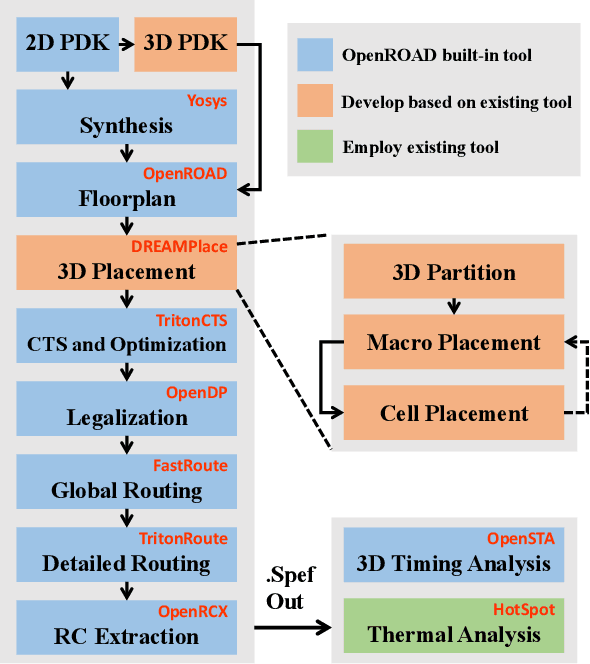
This work introduces Open3DBench, an open-source 3D-IC backend implementation benchmark built upon the OpenROAD-flow-scripts framework, enabling comprehensive evaluation of power, performance, area, and thermal metrics. Our proposed flow supports modular integration of 3D partitioning, placement, 3D routing, RC extraction, and thermal simulation, aligning with advanced 3D flows that rely on commercial tools and in-house scripts. We present two foundational 3D placement algorithms: Open3D-Tiling, which emphasizes regular macro placement, and Open3D-DMP, which enhances wirelength optimization through cross-die co-placement with analytical placer DREAMPlace. Experimental results show significant improvements in area (51.19%), wirelength (24.06%), timing (30.84%), and power (5.72%) compared to 2D flows. The results also highlight that better wirelength does not necessarily lead to PPA gain, emphasizing the need of developing PPA-driven methods. Open3DBench offers a standardized, reproducible platform for evaluating 3D EDA methods, effectively bridging the gap between open-source tools and commercial solutions in 3D-IC design.

Stochastic Population Update Provably Needs An Archive in Evolutionary Multi-objective Optimization

Evolutionary algorithms (EAs) have been widely applied to multi-objective optimization, due to their nature of population-based search. Population update, a key component in multi-objective EAs (MOEAs), is usually performed in a greedy, deterministic manner. However, recent studies have questioned this practice and shown that stochastic population update (SPU), which allows inferior solutions have a chance to be preserved, can help MOEAs jump out of local optima more easily. While introducing randomness in the population update process boosts the exploration of MOEAs, there is a drawback that the population may not always preserve the very best solutions found, thus entailing a large population. Intuitively, a possible solution to this issue is to introduce an archive that stores the best solutions ever found. In this paper, we theoretically show that using an archive can allow a small population and accelerate the search of SPU-based MOEAs substantially. Specifically, we analyze the expected running time of two well-established MOEAs, SMS-EMOA and NSGA-II, with SPU for solving a commonly studied bi-objective problem OneJumpZeroJump, and prove that using an archive can bring (even exponential) speedups. The comparison between SMS-EMOA and NSGA-II also suggests that the $(\mu+\mu)$ update mode may be more suitable for SPU than the $(\mu+1)$ update mode. Furthermore, our derived running time bounds for using SPU alone are significantly tighter than previously known ones. Our theoretical findings are also empirically validated on a well-known practical problem, the multi-objective traveling salesperson problem. We hope this work may provide theoretical support to explore different ideas of designing algorithms in evolutionary multi-objective optimization.

Pareto Set Learning for Multi-Objective Reinforcement Learning

Multi-objective decision-making problems have emerged in numerous real-world scenarios, such as video games, navigation and robotics. Considering the clear advantages of Reinforcement Learning (RL) in optimizing decision-making processes, researchers have delved into the development of Multi-Objective RL (MORL) methods for solving multi-objective decision problems. However, previous methods either cannot obtain the entire Pareto front, or employ only a single policy network for all the preferences over multiple objectives, which may not produce personalized solutions for each preference. To address these limitations, we propose a novel decomposition-based framework for MORL, Pareto Set Learning for MORL (PSL-MORL), that harnesses the generation capability of hypernetwork to produce the parameters of the policy network for each decomposition weight, generating relatively distinct policies for various scalarized subproblems with high efficiency. PSL-MORL is a general framework, which is compatible for any RL algorithm. The theoretical result guarantees the superiority of the model capacity of PSL-MORL and the optimality of the obtained policy network. Through extensive experiments on diverse benchmarks, we demonstrate the effectiveness of PSL-MORL in achieving dense coverage of the Pareto front, significantly outperforming state-of-the-art MORL methods in the hypervolume and sparsity indicators.

Pareto Optimization with Robust Evaluation for Noisy Subset Selection

Subset selection is a fundamental problem in combinatorial optimization, which has a wide range of applications such as influence maximization and sparse regression. The goal is to select a subset of limited size from a ground set in order to maximize a given objective function. However, the evaluation of the objective function in real-world scenarios is often noisy. Previous algorithms, including the greedy algorithm and multi-objective evolutionary algorithms POSS and PONSS, either struggle in noisy environments or consume excessive computational resources. In this paper, we focus on the noisy subset selection problem with a cardinality constraint, where the evaluation of a subset is noisy. We propose a novel approach based on Pareto Optimization with Robust Evaluation for noisy subset selection (PORE), which maximizes a robust evaluation function and minimizes the subset size simultaneously. PORE can efficiently identify well-structured solutions and handle computational resources, addressing the limitations observed in PONSS. Our experiments, conducted on real-world datasets for influence maximization and sparse regression, demonstrate that PORE significantly outperforms previous methods, including the classical greedy algorithm, POSS, and PONSS. Further validation through ablation studies confirms the effectiveness of our robust evaluation function.

Reinforcement Learning Policy as Macro Regulator Rather than Macro Placer

In modern chip design, placement aims at placing millions of circuit modules, which is an essential step that significantly influences power, performance, and area (PPA) metrics. Recently, reinforcement learning (RL) has emerged as a promising technique for improving placement quality, especially macro placement. However, current RL-based placement methods suffer from long training times, low generalization ability, and inability to guarantee PPA results. A key issue lies in the problem formulation, i.e., using RL to place from scratch, which results in limits useful information and inaccurate rewards during the training process. In this work, we propose an approach that utilizes RL for the refinement stage, which allows the RL policy to learn how to adjust existing placement layouts, thereby receiving sufficient information for the policy to act and obtain relatively dense and precise rewards. Additionally, we introduce the concept of regularity during training, which is considered an important metric in the chip design industry but is often overlooked in current RL placement methods. We evaluate our approach on the ISPD 2005 and ICCAD 2015 benchmark, comparing the global half-perimeter wirelength and regularity of our proposed method against several competitive approaches. Besides, we test the PPA performance using commercial software, showing that RL as a regulator can achieve significant PPA improvements. Our RL regulator can fine-tune placements from any method and enhance their quality. Our work opens up new possibilities for the application of RL in placement, providing a more effective and efficient approach to optimizing chip design. Our code is available at \url{https://github.com/lamda-bbo/macro-regulator}.

Monte Carlo Tree Search based Space Transfer for Black-box Optimization

Bayesian optimization (BO) is a popular method for computationally expensive black-box optimization. However, traditional BO methods need to solve new problems from scratch, leading to slow convergence. Recent studies try to extend BO to a transfer learning setup to speed up the optimization, where search space transfer is one of the most promising approaches and has shown impressive performance on many tasks. However, existing search space transfer methods either lack an adaptive mechanism or are not flexible enough, making it difficult to efficiently identify promising search space during the optimization process. In this paper, we propose a search space transfer learning method based on Monte Carlo tree search (MCTS), called MCTS-transfer, to iteratively divide, select, and optimize in a learned subspace. MCTS-transfer can not only provide a well-performing search space for warm-start but also adaptively identify and leverage the information of similar source tasks to reconstruct the search space during the optimization process. Experiments on synthetic functions, real-world problems, Design-Bench and hyper-parameter optimization show that MCTS-transfer can demonstrate superior performance compared to other search space transfer methods under different settings. Our code is available at \url{https://github.com/lamda-bbo/mcts-transfer}.