Shengjie Ren
Not Just for Archiving: Provable Benefits of Reusing the Archive in Evolutionary Multi-objective Optimization
Aug 23, 2025Abstract:Evolutionary Algorithms (EAs) have become the most popular tool for solving widely-existed multi-objective optimization problems. In Multi-Objective EAs (MOEAs), there is increasing interest in using an archive to store non-dominated solutions generated during the search. This approach can 1) mitigate the effects of population oscillation, a common issue in many MOEAs, and 2) allow for the use of smaller, more practical population sizes. In this paper, we analytically show that the archive can even further help MOEAs through reusing its solutions during the process of new solution generation. We first prove that using a small population size alongside an archive (without incorporating archived solutions in the generation process) may fail on certain problems, as the population may remove previously discovered but promising solutions. We then prove that reusing archive solutions can overcome this limitation, resulting in at least a polynomial speedup on the expected running time. Our analysis focuses on the well-established SMS-EMOA algorithm applied to the commonly studied OneJumpZeroJump problem as well as one of its variants. We also show that reusing archive solutions can be better than using a large population size directly. Finally, we show that our theoretical findings can generally hold in practice by experiments on four well-known practical optimization problems -- multi-objective 0-1 Knapsack, TSP, QAP and NK-landscape problems -- with realistic settings.
Stochastic Population Update Provably Needs An Archive in Evolutionary Multi-objective Optimization
Jan 28, 2025


Abstract:Evolutionary algorithms (EAs) have been widely applied to multi-objective optimization, due to their nature of population-based search. Population update, a key component in multi-objective EAs (MOEAs), is usually performed in a greedy, deterministic manner. However, recent studies have questioned this practice and shown that stochastic population update (SPU), which allows inferior solutions have a chance to be preserved, can help MOEAs jump out of local optima more easily. While introducing randomness in the population update process boosts the exploration of MOEAs, there is a drawback that the population may not always preserve the very best solutions found, thus entailing a large population. Intuitively, a possible solution to this issue is to introduce an archive that stores the best solutions ever found. In this paper, we theoretically show that using an archive can allow a small population and accelerate the search of SPU-based MOEAs substantially. Specifically, we analyze the expected running time of two well-established MOEAs, SMS-EMOA and NSGA-II, with SPU for solving a commonly studied bi-objective problem OneJumpZeroJump, and prove that using an archive can bring (even exponential) speedups. The comparison between SMS-EMOA and NSGA-II also suggests that the $(\mu+\mu)$ update mode may be more suitable for SPU than the $(\mu+1)$ update mode. Furthermore, our derived running time bounds for using SPU alone are significantly tighter than previously known ones. Our theoretical findings are also empirically validated on a well-known practical problem, the multi-objective traveling salesperson problem. We hope this work may provide theoretical support to explore different ideas of designing algorithms in evolutionary multi-objective optimization.
A First Running Time Analysis of the Strength Pareto Evolutionary Algorithm 2 (SPEA2)
Jun 23, 2024Abstract:Evolutionary algorithms (EAs) have emerged as a predominant approach for addressing multi-objective optimization problems. However, the theoretical foundation of multi-objective EAs (MOEAs), particularly the fundamental aspects like running time analysis, remains largely underexplored. Existing theoretical studies mainly focus on basic MOEAs, with little attention given to practical MOEAs. In this paper, we present a running time analysis of strength Pareto evolutionary algorithm 2 (SPEA2) for the first time. Specifically, we prove that the expected running time of SPEA2 for solving three commonly used multi-objective problems, i.e., $m$OneMinMax, $m$LeadingOnesTrailingZeroes, and $m$-OneJumpZeroJump, is $O(\mu n\cdot \min\{m\log n, n\})$, $O(\mu n^2)$, and $O(\mu n^k \cdot \min\{mn, 3^{m/2}\})$, respectively. Here $m$ denotes the number of objectives, and the population size $\mu$ is required to be at least $(2n/m+1)^{m/2}$, $(2n/m+1)^{m-1}$ and $(2n/m-2k+3)^{m/2}$, respectively. The proofs are accomplished through general theorems which are also applicable for analyzing the expected running time of other MOEAs on these problems, and thus can be helpful for future theoretical analysis of MOEAs.
Maintaining Diversity Provably Helps in Evolutionary Multimodal Optimization
Jun 04, 2024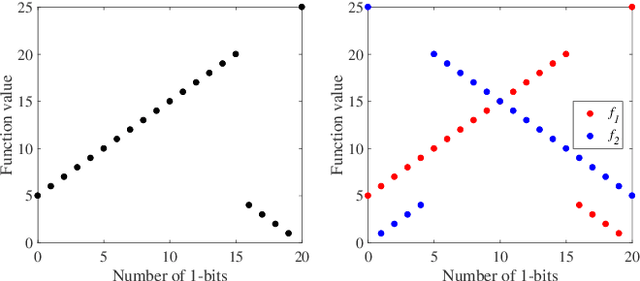
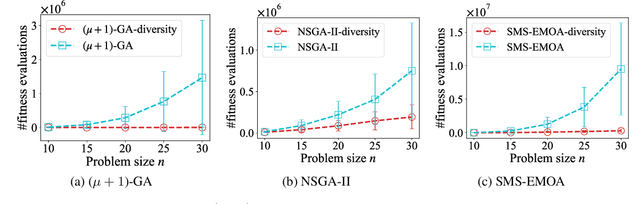
Abstract:In the real world, there exist a class of optimization problems that multiple (local) optimal solutions in the solution space correspond to a single point in the objective space. In this paper, we theoretically show that for such multimodal problems, a simple method that considers the diversity of solutions in the solution space can benefit the search in evolutionary algorithms (EAs). Specifically, we prove that the proposed method, working with crossover, can help enhance the exploration, leading to polynomial or even exponential acceleration on the expected running time. This result is derived by rigorous running time analysis in both single-objective and multi-objective scenarios, including $(\mu+1)$-GA solving the widely studied single-objective problem, Jump, and NSGA-II and SMS-EMOA (two well-established multi-objective EAs) solving the widely studied bi-objective problem, OneJumpZeroJump. Experiments are also conducted to validate the theoretical results. We hope that our results may encourage the exploration of diversity maintenance in the solution space for multi-objective optimization, where existing EAs usually only consider the diversity in the objective space and can easily be trapped in local optima.
An Archive Can Bring Provable Speed-ups in Multi-Objective Evolutionary Algorithms
Jun 04, 2024Abstract:In the area of multi-objective evolutionary algorithms (MOEAs), there is a trend of using an archive to store non-dominated solutions generated during the search. This is because 1) MOEAs may easily end up with the final population containing inferior solutions that are dominated by other solutions discarded during the search process and 2) the population that has a commensurable size of the problem's Pareto front is often not practical. In this paper, we theoretically show, for the first time, that using an archive can guarantee speed-ups for MOEAs. Specifically, we prove that for two well-established MOEAs (NSGA-II and SMS-EMOA) on two commonly studied problems (OneMinMax and LeadingOnesTrailingZeroes), using an archive brings a polynomial acceleration on the expected running time. The reason is that with an archive, the size of the population can reduce to a small constant; there is no need for the population to keep all the Pareto optimal solutions found. This contrasts existing theoretical studies for MOEAs where a population with a commensurable size of the problem's Pareto front is needed. The findings in this paper not only provide a theoretical confirmation for an increasingly popular practice in the design of MOEAs, but can also be beneficial to the theory community towards studying more practical MOEAs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge