Quality-Diversity Red-Teaming: Automated Generation of High-Quality and Diverse Attackers for Large Language Models

Ensuring safety of large language models (LLMs) is important. Red teaming--a systematic approach to identifying adversarial prompts that elicit harmful responses from target LLMs--has emerged as a crucial safety evaluation method. Within this framework, the diversity of adversarial prompts is essential for comprehensive safety assessments. We find that previous approaches to red-teaming may suffer from two key limitations. First, they often pursue diversity through simplistic metrics like word frequency or sentence embedding similarity, which may not capture meaningful variation in attack strategies. Second, the common practice of training a single attacker model restricts coverage across potential attack styles and risk categories. This paper introduces Quality-Diversity Red-Teaming (QDRT), a new framework designed to address these limitations. QDRT achieves goal-driven diversity through behavior-conditioned training and implements a behavioral replay buffer in an open-ended manner. Additionally, it trains multiple specialized attackers capable of generating high-quality attacks across diverse styles and risk categories. Our empirical evaluation demonstrates that QDRT generates attacks that are both more diverse and more effective against a wide range of target LLMs, including GPT-2, Llama-3, Gemma-2, and Qwen2.5. This work advances the field of LLM safety by providing a systematic and effective approach to automated red-teaming, ultimately supporting the responsible deployment of LLMs.

Pareto Set Learning for Multi-Objective Reinforcement Learning

Multi-objective decision-making problems have emerged in numerous real-world scenarios, such as video games, navigation and robotics. Considering the clear advantages of Reinforcement Learning (RL) in optimizing decision-making processes, researchers have delved into the development of Multi-Objective RL (MORL) methods for solving multi-objective decision problems. However, previous methods either cannot obtain the entire Pareto front, or employ only a single policy network for all the preferences over multiple objectives, which may not produce personalized solutions for each preference. To address these limitations, we propose a novel decomposition-based framework for MORL, Pareto Set Learning for MORL (PSL-MORL), that harnesses the generation capability of hypernetwork to produce the parameters of the policy network for each decomposition weight, generating relatively distinct policies for various scalarized subproblems with high efficiency. PSL-MORL is a general framework, which is compatible for any RL algorithm. The theoretical result guarantees the superiority of the model capacity of PSL-MORL and the optimality of the obtained policy network. Through extensive experiments on diverse benchmarks, we demonstrate the effectiveness of PSL-MORL in achieving dense coverage of the Pareto front, significantly outperforming state-of-the-art MORL methods in the hypervolume and sparsity indicators.

Quality-Diversity with Limited Resources

Quality-Diversity (QD) algorithms have emerged as a powerful optimization paradigm with the aim of generating a set of high-quality and diverse solutions. To achieve such a challenging goal, QD algorithms require maintaining a large archive and a large population in each iteration, which brings two main issues, sample and resource efficiency. Most advanced QD algorithms focus on improving the sample efficiency, while the resource efficiency is overlooked to some extent. Particularly, the resource overhead during the training process has not been touched yet, hindering the wider application of QD algorithms. In this paper, we highlight this important research question, i.e., how to efficiently train QD algorithms with limited resources, and propose a novel and effective method called RefQD to address it. RefQD decomposes a neural network into representation and decision parts, and shares the representation part with all decision parts in the archive to reduce the resource overhead. It also employs a series of strategies to address the mismatch issue between the old decision parts and the newly updated representation part. Experiments on different types of tasks from small to large resource consumption demonstrate the excellent performance of RefQD: it not only uses significantly fewer resources (e.g., 16\% GPU memories on QDax and 3.7\% on Atari) but also achieves comparable or better performance compared to sample-efficient QD algorithms. Our code is available at \url{https://github.com/lamda-bbo/RefQD}.

Quality-Diversity Algorithms Can Provably Be Helpful for Optimization

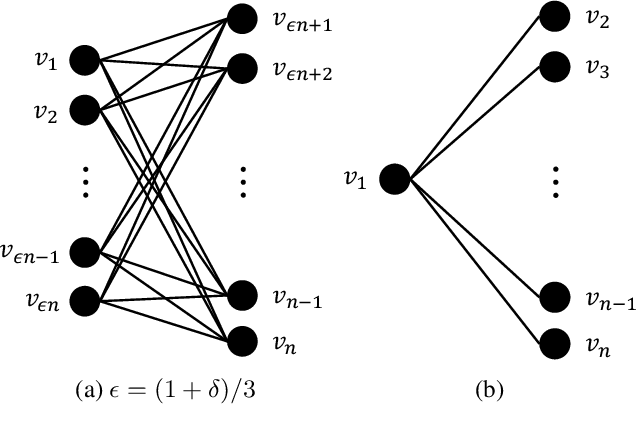
Quality-Diversity (QD) algorithms are a new type of Evolutionary Algorithms (EAs), aiming to find a set of high-performing, yet diverse solutions. They have found many successful applications in reinforcement learning and robotics, helping improve the robustness in complex environments. Furthermore, they often empirically find a better overall solution than traditional search algorithms which explicitly search for a single highest-performing solution. However, their theoretical analysis is far behind, leaving many fundamental questions unexplored. In this paper, we try to shed some light on the optimization ability of QD algorithms via rigorous running time analysis. By comparing the popular QD algorithm MAP-Elites with $(\mu+1)$-EA (a typical EA focusing on finding better objective values only), we prove that on two NP-hard problem classes with wide applications, i.e., monotone approximately submodular maximization with a size constraint, and set cover, MAP-Elites can achieve the (asymptotically) optimal polynomial-time approximation ratio, while $(\mu+1)$-EA requires exponential expected time on some instances. This provides theoretical justification for that QD algorithms can be helpful for optimization, and discloses that the simultaneous search for high-performing solutions with diverse behaviors can provide stepping stones to good overall solutions and help avoid local optima.

Diversity from Human Feedback

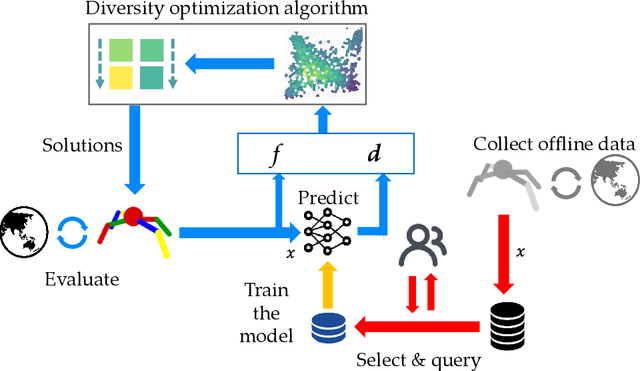
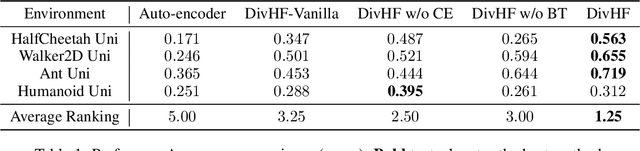
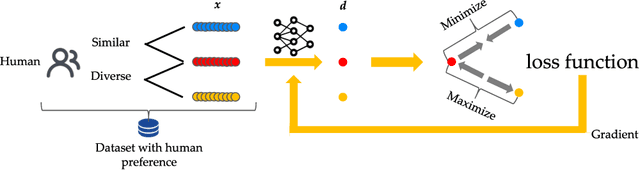
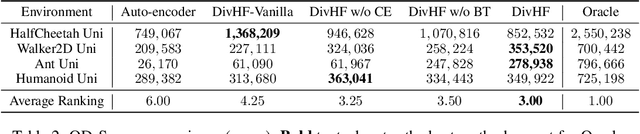
Diversity plays a significant role in many problems, such as ensemble learning, reinforcement learning, and combinatorial optimization. How to define the diversity measure is a longstanding problem. Many methods rely on expert experience to define a proper behavior space and then obtain the diversity measure, which is, however, challenging in many scenarios. In this paper, we propose the problem of learning a behavior space from human feedback and present a general method called Diversity from Human Feedback (DivHF) to solve it. DivHF learns a behavior descriptor consistent with human preference by querying human feedback. The learned behavior descriptor can be combined with any distance measure to define a diversity measure. We demonstrate the effectiveness of DivHF by integrating it with the Quality-Diversity optimization algorithm MAP-Elites and conducting experiments on the QDax suite. The results show that DivHF learns a behavior space that aligns better with human requirements compared to direct data-driven approaches and leads to more diverse solutions under human preference. Our contributions include formulating the problem, proposing the DivHF method, and demonstrating its effectiveness through experiments.