Best Practices For Empirical Meta-Algorithmic Research: Guidelines from the COSEAL Research Network

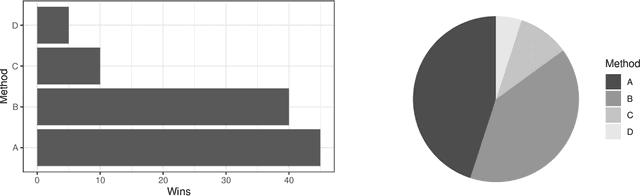
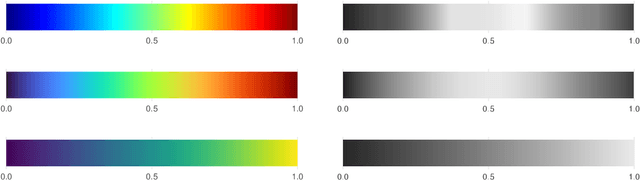
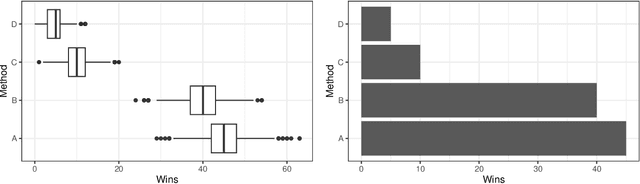
Empirical research on meta-algorithmics, such as algorithm selection, configuration, and scheduling, often relies on extensive and thus computationally expensive experiments. With the large degree of freedom we have over our experimental setup and design comes a plethora of possible error sources that threaten the scalability and validity of our scientific insights. Best practices for meta-algorithmic research exist, but they are scattered between different publications and fields, and continue to evolve separately from each other. In this report, we collect good practices for empirical meta-algorithmic research across the subfields of the COSEAL community, encompassing the entire experimental cycle: from formulating research questions and selecting an experimental design, to executing experiments, and ultimately, analyzing and presenting results impartially. It establishes the current state-of-the-art practices within meta-algorithmic research and serves as a guideline to both new researchers and practitioners in meta-algorithmic fields.

Re$^{\text{2}}$MaP: Macro Placement by Recursively Prototyping and Packing Tree-based Relocating

This work introduces the Re$^{\text{2}}$MaP method, which generates expert-quality macro placements through recursively prototyping and packing tree-based relocating. We first perform multi-level macro grouping and PPA-aware cell clustering to produce a unified connection matrix that captures both wirelength and dataflow among macros and clusters. Next, we use DREAMPlace to build a mixed-size placement prototype and obtain reference positions for each macro and cluster. Based on this prototype, we introduce ABPlace, an angle-based analytical method that optimizes macro positions on an ellipse to distribute macros uniformly near chip periphery, while optimizing wirelength and dataflow. A packing tree-based relocating procedure is then designed to jointly adjust the locations of macro groups and the macros within each group, by optimizing an expertise-inspired cost function that captures various design constraints through evolutionary search. Re$^{\text{2}}$MaP repeats the above process: Only a subset of macro groups are positioned in each iteration, and the remaining macros are deferred to the next iteration to improve the prototype's accuracy. Using a well-established backend flow with sufficient timing optimizations, Re$^{\text{2}}$MaP achieves up to 22.22% (average 10.26%) improvement in worst negative slack (WNS) and up to 97.91% (average 33.97%) improvement in total negative slack (TNS) compared to the state-of-the-art academic placer Hier-RTLMP. It also ranks higher on WNS, TNS, power, design rule check (DRC) violations, and runtime than the conference version ReMaP, across seven tested cases. Our code is available at https://github.com/lamda-bbo/Re2MaP.

Towards Universal Offline Black-Box Optimization via Learning Language Model Embeddings

The pursuit of universal black-box optimization (BBO) algorithms is a longstanding goal. However, unlike domains such as language or vision, where scaling structured data has driven generalization, progress in offline BBO remains hindered by the lack of unified representations for heterogeneous numerical spaces. Thus, existing offline BBO approaches are constrained to single-task and fixed-dimensional settings, failing to achieve cross-domain universal optimization. Recent advances in language models (LMs) offer a promising path forward: their embeddings capture latent relationships in a unifying way, enabling universal optimization across different data types possible. In this paper, we discuss multiple potential approaches, including an end-to-end learning framework in the form of next-token prediction, as well as prioritizing the learning of latent spaces with strong representational capabilities. To validate the effectiveness of these methods, we collect offline BBO tasks and data from open-source academic works for training. Experiments demonstrate the universality and effectiveness of our proposed methods. Our findings suggest that unifying language model priors and learning string embedding space can overcome traditional barriers in universal BBO, paving the way for general-purpose BBO algorithms. The code is provided at https://github.com/lamda-bbo/universal-offline-bbo.

Quality-Diversity Red-Teaming: Automated Generation of High-Quality and Diverse Attackers for Large Language Models

Ensuring safety of large language models (LLMs) is important. Red teaming--a systematic approach to identifying adversarial prompts that elicit harmful responses from target LLMs--has emerged as a crucial safety evaluation method. Within this framework, the diversity of adversarial prompts is essential for comprehensive safety assessments. We find that previous approaches to red-teaming may suffer from two key limitations. First, they often pursue diversity through simplistic metrics like word frequency or sentence embedding similarity, which may not capture meaningful variation in attack strategies. Second, the common practice of training a single attacker model restricts coverage across potential attack styles and risk categories. This paper introduces Quality-Diversity Red-Teaming (QDRT), a new framework designed to address these limitations. QDRT achieves goal-driven diversity through behavior-conditioned training and implements a behavioral replay buffer in an open-ended manner. Additionally, it trains multiple specialized attackers capable of generating high-quality attacks across diverse styles and risk categories. Our empirical evaluation demonstrates that QDRT generates attacks that are both more diverse and more effective against a wide range of target LLMs, including GPT-2, Llama-3, Gemma-2, and Qwen2.5. This work advances the field of LLM safety by providing a systematic and effective approach to automated red-teaming, ultimately supporting the responsible deployment of LLMs.

Open3DBench: Open-Source Benchmark for 3D-IC Backend Implementation and PPA Evaluation

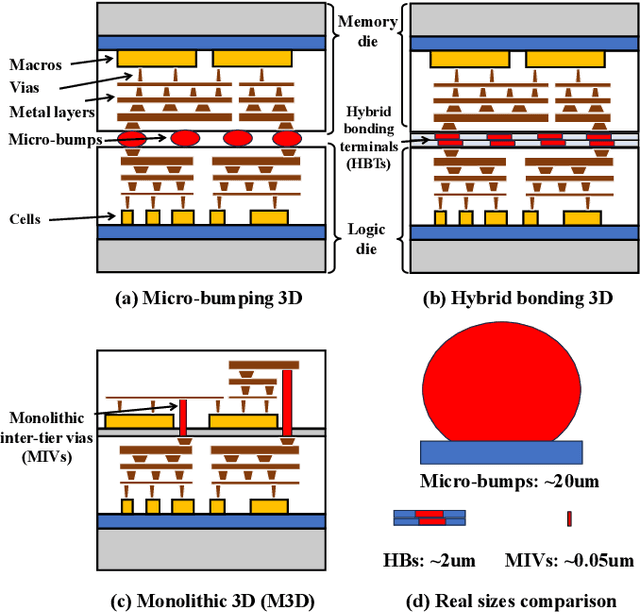
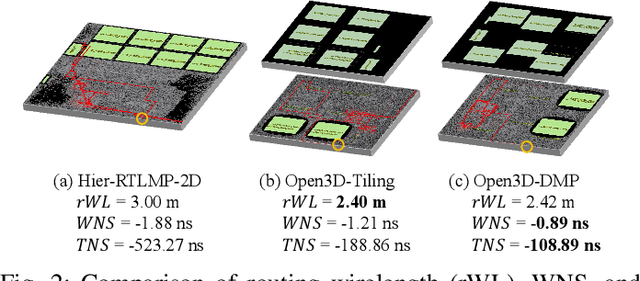
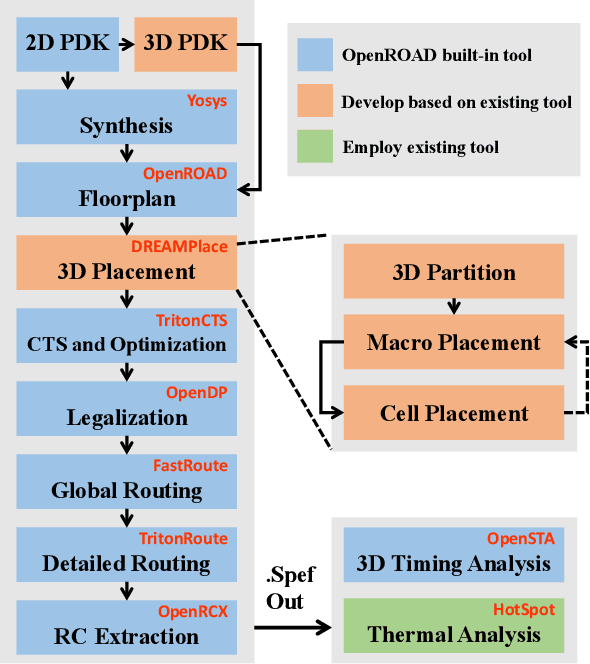
This work introduces Open3DBench, an open-source 3D-IC backend implementation benchmark built upon the OpenROAD-flow-scripts framework, enabling comprehensive evaluation of power, performance, area, and thermal metrics. Our proposed flow supports modular integration of 3D partitioning, placement, 3D routing, RC extraction, and thermal simulation, aligning with advanced 3D flows that rely on commercial tools and in-house scripts. We present two foundational 3D placement algorithms: Open3D-Tiling, which emphasizes regular macro placement, and Open3D-DMP, which enhances wirelength optimization through cross-die co-placement with analytical placer DREAMPlace. Experimental results show significant improvements in area (51.19%), wirelength (24.06%), timing (30.84%), and power (5.72%) compared to 2D flows. The results also highlight that better wirelength does not necessarily lead to PPA gain, emphasizing the need of developing PPA-driven methods. Open3DBench offers a standardized, reproducible platform for evaluating 3D EDA methods, effectively bridging the gap between open-source tools and commercial solutions in 3D-IC design.

DualStream Contextual Fusion Network: Efficient Target Speaker Extraction by Leveraging Mixture and Enrollment Interactions

Target speaker extraction focuses on extracting a target speech signal from an environment with multiple speakers by leveraging an enrollment. Existing methods predominantly rely on speaker embeddings obtained from the enrollment, potentially disregarding the contextual information and the internal interactions between the mixture and enrollment. In this paper, we propose a novel DualStream Contextual Fusion Network (DCF-Net) in the time-frequency (T-F) domain. Specifically, DualStream Fusion Block (DSFB) is introduced to obtain contextual information and capture the interactions between contextualized enrollment and mixture representation across both spatial and channel dimensions, and then rich and consistent representations are utilized to guide the extraction network for better extraction. Experimental results demonstrate that DCF-Net outperforms state-of-the-art (SOTA) methods, achieving a scale-invariant signal-to-distortion ratio improvement (SI-SDRi) of 21.6 dB on the benchmark dataset, and exhibits its robustness and effectiveness in both noise and reverberation scenarios. In addition, the wrong extraction results of our model, called target confusion problem, reduce to 0.4%, which highlights the potential of DCF-Net for practical applications.

Pareto Set Learning for Multi-Objective Reinforcement Learning

Multi-objective decision-making problems have emerged in numerous real-world scenarios, such as video games, navigation and robotics. Considering the clear advantages of Reinforcement Learning (RL) in optimizing decision-making processes, researchers have delved into the development of Multi-Objective RL (MORL) methods for solving multi-objective decision problems. However, previous methods either cannot obtain the entire Pareto front, or employ only a single policy network for all the preferences over multiple objectives, which may not produce personalized solutions for each preference. To address these limitations, we propose a novel decomposition-based framework for MORL, Pareto Set Learning for MORL (PSL-MORL), that harnesses the generation capability of hypernetwork to produce the parameters of the policy network for each decomposition weight, generating relatively distinct policies for various scalarized subproblems with high efficiency. PSL-MORL is a general framework, which is compatible for any RL algorithm. The theoretical result guarantees the superiority of the model capacity of PSL-MORL and the optimality of the obtained policy network. Through extensive experiments on diverse benchmarks, we demonstrate the effectiveness of PSL-MORL in achieving dense coverage of the Pareto front, significantly outperforming state-of-the-art MORL methods in the hypervolume and sparsity indicators.

Reinforcement Learning Policy as Macro Regulator Rather than Macro Placer

In modern chip design, placement aims at placing millions of circuit modules, which is an essential step that significantly influences power, performance, and area (PPA) metrics. Recently, reinforcement learning (RL) has emerged as a promising technique for improving placement quality, especially macro placement. However, current RL-based placement methods suffer from long training times, low generalization ability, and inability to guarantee PPA results. A key issue lies in the problem formulation, i.e., using RL to place from scratch, which results in limits useful information and inaccurate rewards during the training process. In this work, we propose an approach that utilizes RL for the refinement stage, which allows the RL policy to learn how to adjust existing placement layouts, thereby receiving sufficient information for the policy to act and obtain relatively dense and precise rewards. Additionally, we introduce the concept of regularity during training, which is considered an important metric in the chip design industry but is often overlooked in current RL placement methods. We evaluate our approach on the ISPD 2005 and ICCAD 2015 benchmark, comparing the global half-perimeter wirelength and regularity of our proposed method against several competitive approaches. Besides, we test the PPA performance using commercial software, showing that RL as a regulator can achieve significant PPA improvements. Our RL regulator can fine-tune placements from any method and enhance their quality. Our work opens up new possibilities for the application of RL in placement, providing a more effective and efficient approach to optimizing chip design. Our code is available at \url{https://github.com/lamda-bbo/macro-regulator}.

Monte Carlo Tree Search based Space Transfer for Black-box Optimization

Bayesian optimization (BO) is a popular method for computationally expensive black-box optimization. However, traditional BO methods need to solve new problems from scratch, leading to slow convergence. Recent studies try to extend BO to a transfer learning setup to speed up the optimization, where search space transfer is one of the most promising approaches and has shown impressive performance on many tasks. However, existing search space transfer methods either lack an adaptive mechanism or are not flexible enough, making it difficult to efficiently identify promising search space during the optimization process. In this paper, we propose a search space transfer learning method based on Monte Carlo tree search (MCTS), called MCTS-transfer, to iteratively divide, select, and optimize in a learned subspace. MCTS-transfer can not only provide a well-performing search space for warm-start but also adaptively identify and leverage the information of similar source tasks to reconstruct the search space during the optimization process. Experiments on synthetic functions, real-world problems, Design-Bench and hyper-parameter optimization show that MCTS-transfer can demonstrate superior performance compared to other search space transfer methods under different settings. Our code is available at \url{https://github.com/lamda-bbo/mcts-transfer}.

Offline Model-Based Optimization by Learning to Rank

Offline model-based optimization (MBO) aims to identify a design that maximizes a black-box function using only a fixed, pre-collected dataset of designs and their corresponding scores. A common approach in offline MBO is to train a regression-based surrogate model by minimizing mean squared error (MSE) and then find the best design within this surrogate model by different optimizers (e.g., gradient ascent). However, a critical challenge is the risk of out-of-distribution errors, i.e., the surrogate model may typically overestimate the scores and mislead the optimizers into suboptimal regions. Prior works have attempted to address this issue in various ways, such as using regularization techniques and ensemble learning to enhance the robustness of the model, but it still remains. In this paper, we argue that regression models trained with MSE are not well-aligned with the primary goal of offline MBO, which is to select promising designs rather than to predict their scores precisely. Notably, if a surrogate model can maintain the order of candidate designs based on their relative score relationships, it can produce the best designs even without precise predictions. To validate it, we conduct experiments to compare the relationship between the quality of the final designs and MSE, finding that the correlation is really very weak. In contrast, a metric that measures order-maintaining quality shows a significantly stronger correlation. Based on this observation, we propose learning a ranking-based model that leverages learning to rank techniques to prioritize promising designs based on their relative scores. We show that the generalization error on ranking loss can be well bounded. Empirical results across diverse tasks demonstrate the superior performance of our proposed ranking-based models than twenty existing methods.