Pareto Optimization with Robust Evaluation for Noisy Subset Selection

Subset selection is a fundamental problem in combinatorial optimization, which has a wide range of applications such as influence maximization and sparse regression. The goal is to select a subset of limited size from a ground set in order to maximize a given objective function. However, the evaluation of the objective function in real-world scenarios is often noisy. Previous algorithms, including the greedy algorithm and multi-objective evolutionary algorithms POSS and PONSS, either struggle in noisy environments or consume excessive computational resources. In this paper, we focus on the noisy subset selection problem with a cardinality constraint, where the evaluation of a subset is noisy. We propose a novel approach based on Pareto Optimization with Robust Evaluation for noisy subset selection (PORE), which maximizes a robust evaluation function and minimizes the subset size simultaneously. PORE can efficiently identify well-structured solutions and handle computational resources, addressing the limitations observed in PONSS. Our experiments, conducted on real-world datasets for influence maximization and sparse regression, demonstrate that PORE significantly outperforms previous methods, including the classical greedy algorithm, POSS, and PONSS. Further validation through ablation studies confirms the effectiveness of our robust evaluation function.

Biased Pareto Optimization for Subset Selection with Dynamic Cost Constraints

Subset selection with cost constraints aims to select a subset from a ground set to maximize a monotone objective function without exceeding a given budget, which has various applications such as influence maximization and maximum coverage. In real-world scenarios, the budget, representing available resources, may change over time, which requires that algorithms must adapt quickly to new budgets. However, in this dynamic environment, previous algorithms either lack theoretical guarantees or require a long running time. The state-of-the-art algorithm, POMC, is a Pareto optimization approach designed for static problems, lacking consideration for dynamic problems. In this paper, we propose BPODC, enhancing POMC with biased selection and warm-up strategies tailored for dynamic environments. We focus on the ability of BPODC to leverage existing computational results while adapting to budget changes. We prove that BPODC can maintain the best known $(\alpha_f/2)(1-e^{-\alpha_f})$-approximation guarantee when the budget changes. Experiments on influence maximization and maximum coverage show that BPODC adapts more effectively and rapidly to budget changes, with a running time that is less than that of the static greedy algorithm.

Peptide Vaccine Design by Evolutionary Multi-Objective Optimization

Peptide vaccines are growing in significance for fighting diverse diseases. Machine learning has improved the identification of peptides that can trigger immune responses, and the main challenge of peptide vaccine design now lies in selecting an effective subset of peptides due to the allelic diversity among individuals. Previous works mainly formulated this task as a constrained optimization problem, aiming to maximize the expected number of peptide-Major Histocompatibility Complex (peptide-MHC) bindings across a broad range of populations by selecting a subset of diverse peptides with limited size; and employed a greedy algorithm, whose performance, however, may be limited due to the greedy nature. In this paper, we propose a new framework PVD-EMO based on Evolutionary Multi-objective Optimization, which reformulates Peptide Vaccine Design as a bi-objective optimization problem that maximizes the expected number of peptide-MHC bindings and minimizes the number of selected peptides simultaneously, and employs a Multi-Objective Evolutionary Algorithm (MOEA) to solve it. We also incorporate warm-start and repair strategies into MOEAs to improve efficiency and performance. We prove that the warm-start strategy ensures that PVD-EMO maintains the same worst-case approximation guarantee as the previous greedy algorithm, and meanwhile, the EMO framework can help avoid local optima. Experiments on a peptide vaccine design for COVID-19, caused by the SARS-CoV-2 virus, demonstrate the superiority of PVD-EMO.

Migrant Resettlement by Evolutionary Multi-objective Optimization

Migration has been a universal phenomenon, which brings opportunities as well as challenges for global development. As the number of migrants (e.g., refugees) increases rapidly in recent years, a key challenge faced by each country is the problem of migrant resettlement. This problem has attracted scientific research attention, from the perspective of maximizing the employment rate. Previous works mainly formulated migrant resettlement as an approximately submodular optimization problem subject to multiple matroid constraints and employed the greedy algorithm, whose performance, however, may be limited due to its greedy nature. In this paper, we propose a new framework MR-EMO based on Evolutionary Multi-objective Optimization, which reformulates Migrant Resettlement as a bi-objective optimization problem that maximizes the expected number of employed migrants and minimizes the number of dispatched migrants simultaneously, and employs a Multi-Objective Evolutionary Algorithm (MOEA) to solve the bi-objective problem. We implement MR-EMO using three MOEAs, the popular NSGA-II, MOEA/D as well as the theoretically grounded GSEMO. To further improve the performance of MR-EMO, we propose a specific MOEA, called GSEMO-SR, using matrix-swap mutation and repair mechanism, which has a better ability to search for feasible solutions. We prove that MR-EMO using either GSEMO or GSEMO-SR can achieve better theoretical guarantees than the previous greedy algorithm. Experimental results under the interview and coordination migration models clearly show the superiority of MR-EMO (with either NSGA-II, MOEA/D, GSEMO or GSEMO-SR) over previous algorithms, and that using GSEMO-SR leads to the best performance of MR-EMO.

Result Diversification by Multi-objective Evolutionary Algorithms with Theoretical Guarantees

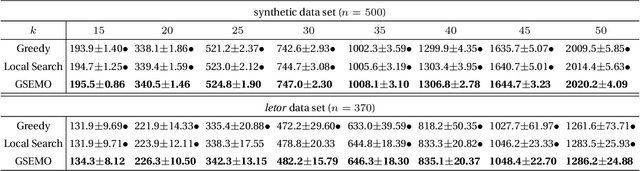
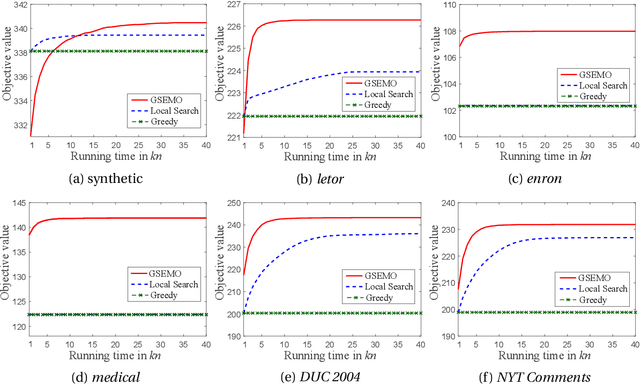
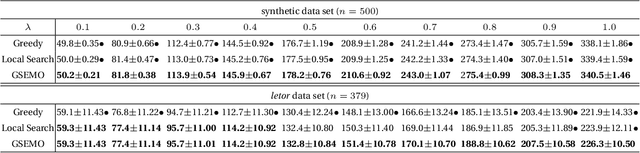
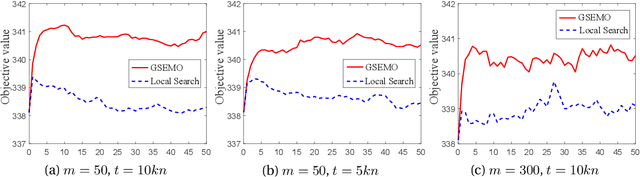
Given a ground set of items, the result diversification problem aims to select a subset with high "quality" and "diversity" while satisfying some constraints. It arises in various real-world artificial intelligence applications, such as web-based search, document summarization and feature selection, and also has applications in other areas, e.g., computational geometry, databases, finance and operations research. Previous algorithms are mainly based on greedy or local search. In this paper, we propose to reformulate the result diversification problem as a bi-objective maximization problem, and solve it by a multi-objective evolutionary algorithm (EA), i.e., the GSEMO. We theoretically prove that the GSEMO can achieve the (asymptotically) optimal theoretical guarantees under both static and dynamic environments. For cardinality constraints, the GSEMO can achieve the optimal polynomial-time approximation ratio, $1/2$. For more general matroid constraints, the GSEMO can achieve the asymptotically optimal polynomial-time approximation ratio, $1/2-\epsilon/(4n)$. Furthermore, when the objective function (i.e., a linear combination of quality and diversity) changes dynamically, the GSEMO can maintain this approximation ratio in polynomial running time, addressing the open question proposed by Borodin et al. This also theoretically shows the superiority of EAs over local search for solving dynamic optimization problems for the first time, and discloses the robustness of the mutation operator of EAs against dynamic changes. Experiments on the applications of web-based search, multi-label feature selection and document summarization show the superior performance of the GSEMO over the state-of-the-art algorithms (i.e., the greedy algorithm and local search) under both static and dynamic environments.

Multi-objective Evolutionary Algorithms are Generally Good: Maximizing Monotone Submodular Functions over Sequences

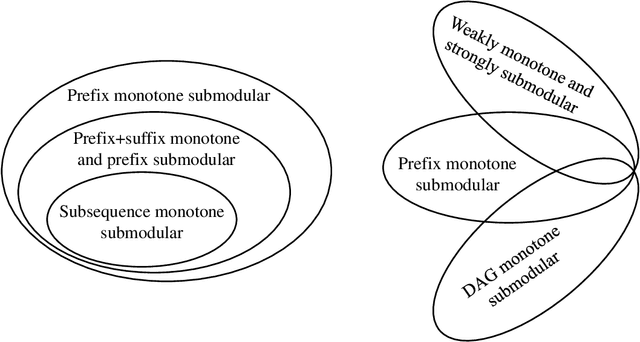
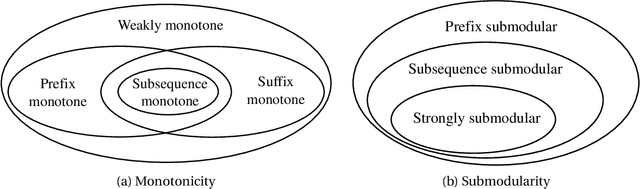
Evolutionary algorithms (EAs) are general-purpose optimization algorithms, inspired by natural evolution. Recent theoretical studies have shown that EAs can achieve good approximation guarantees for solving the problem classes of submodular optimization, which have a wide range of applications, such as maximum coverage, sparse regression, influence maximization, document summarization and sensor placement, just to name a few. Though they have provided some theoretical explanation for the general-purpose nature of EAs, the considered submodular objective functions are defined only over sets or multisets. To complement this line of research, this paper studies the problem class of maximizing monotone submodular functions over sequences, where the objective function depends on the order of items. We prove that for each kind of previously studied monotone submodular objective functions over sequences, i.e., prefix monotone submodular functions, weakly monotone and strongly submodular functions, and DAG monotone submodular functions, a simple multi-objective EA, i.e., GSEMO, can always reach or improve the best known approximation guarantee after running polynomial time in expectation. Note that these best-known approximation guarantees can be obtained only by different greedy-style algorithms before. Empirical studies on various applications, e.g., accomplishing tasks, maximizing information gain, search-and-tracking and recommender systems, show the excellent performance of the GSEMO.