Migrant Resettlement by Evolutionary Multi-objective Optimization

Migration has been a universal phenomenon, which brings opportunities as well as challenges for global development. As the number of migrants (e.g., refugees) increases rapidly in recent years, a key challenge faced by each country is the problem of migrant resettlement. This problem has attracted scientific research attention, from the perspective of maximizing the employment rate. Previous works mainly formulated migrant resettlement as an approximately submodular optimization problem subject to multiple matroid constraints and employed the greedy algorithm, whose performance, however, may be limited due to its greedy nature. In this paper, we propose a new framework MR-EMO based on Evolutionary Multi-objective Optimization, which reformulates Migrant Resettlement as a bi-objective optimization problem that maximizes the expected number of employed migrants and minimizes the number of dispatched migrants simultaneously, and employs a Multi-Objective Evolutionary Algorithm (MOEA) to solve the bi-objective problem. We implement MR-EMO using three MOEAs, the popular NSGA-II, MOEA/D as well as the theoretically grounded GSEMO. To further improve the performance of MR-EMO, we propose a specific MOEA, called GSEMO-SR, using matrix-swap mutation and repair mechanism, which has a better ability to search for feasible solutions. We prove that MR-EMO using either GSEMO or GSEMO-SR can achieve better theoretical guarantees than the previous greedy algorithm. Experimental results under the interview and coordination migration models clearly show the superiority of MR-EMO (with either NSGA-II, MOEA/D, GSEMO or GSEMO-SR) over previous algorithms, and that using GSEMO-SR leads to the best performance of MR-EMO.

Submodular Maximization under the Intersection of Matroid and Knapsack Constraints

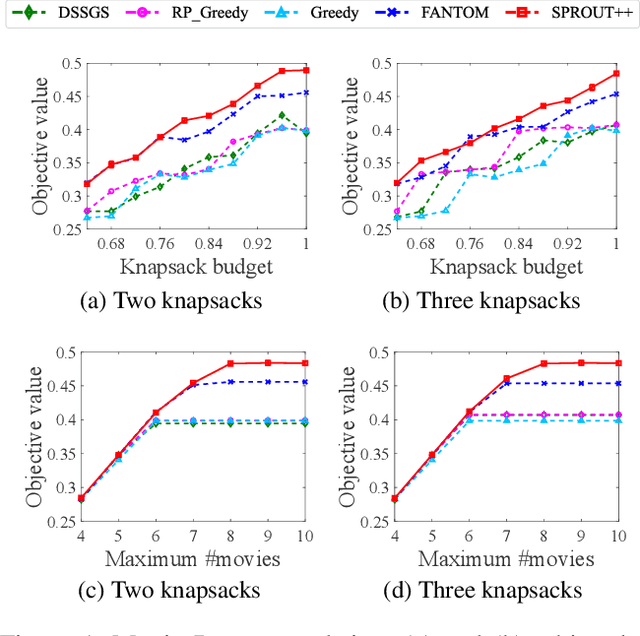
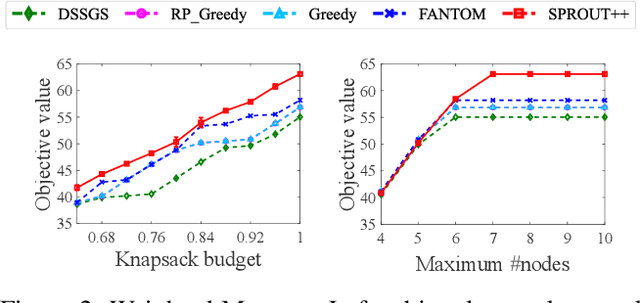
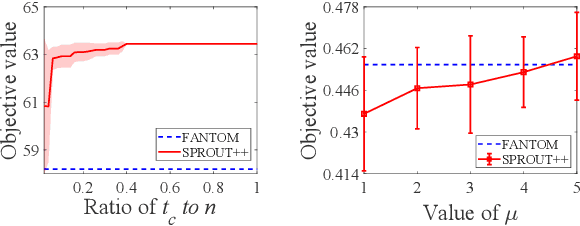
Submodular maximization arises in many applications, and has attracted a lot of research attentions from various areas such as artificial intelligence, finance and operations research. Previous studies mainly consider only one kind of constraint, while many real-world problems often involve several constraints. In this paper, we consider the problem of submodular maximization under the intersection of two commonly used constraints, i.e., $k$-matroid constraint and $m$-knapsack constraint, and propose a new algorithm SPROUT by incorporating partial enumeration into the simultaneous greedy framework. We prove that SPROUT can achieve a polynomial-time approximation guarantee better than the state-of-the-art algorithms. Then, we introduce the random enumeration and smooth techniques into SPROUT to improve its efficiency, resulting in the SPROUT++ algorithm, which can keep a similar approximation guarantee. Experiments on the applications of movie recommendation and weighted max-cut demonstrate the superiority of SPROUT++ in practice.