Submodular Maximization under the Intersection of Matroid and Knapsack Constraints
Paper and Code
Jul 18, 2023
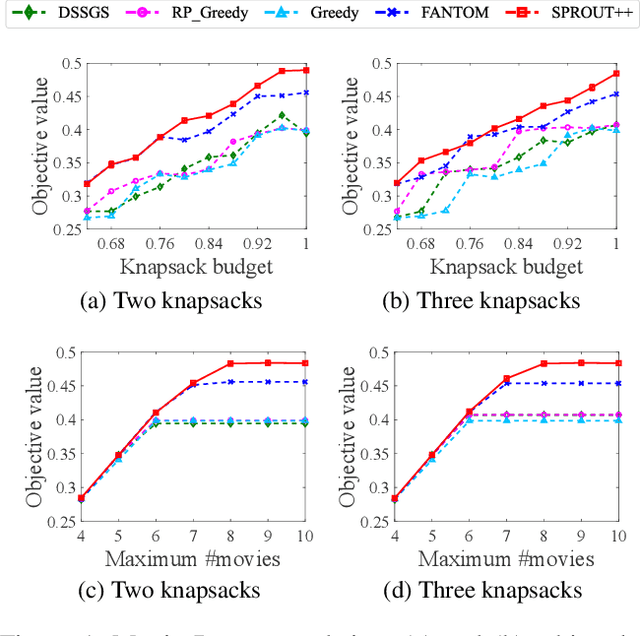
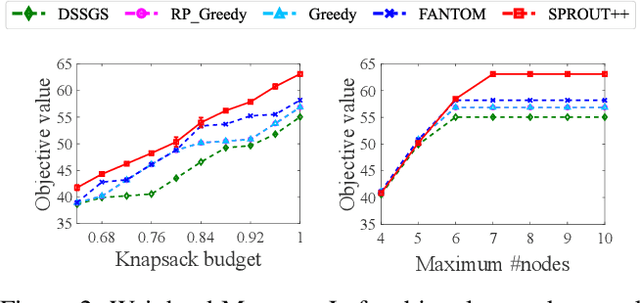
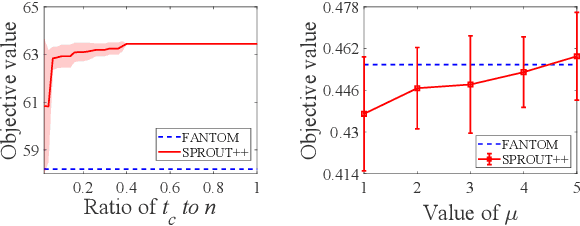
Submodular maximization arises in many applications, and has attracted a lot of research attentions from various areas such as artificial intelligence, finance and operations research. Previous studies mainly consider only one kind of constraint, while many real-world problems often involve several constraints. In this paper, we consider the problem of submodular maximization under the intersection of two commonly used constraints, i.e., $k$-matroid constraint and $m$-knapsack constraint, and propose a new algorithm SPROUT by incorporating partial enumeration into the simultaneous greedy framework. We prove that SPROUT can achieve a polynomial-time approximation guarantee better than the state-of-the-art algorithms. Then, we introduce the random enumeration and smooth techniques into SPROUT to improve its efficiency, resulting in the SPROUT++ algorithm, which can keep a similar approximation guarantee. Experiments on the applications of movie recommendation and weighted max-cut demonstrate the superiority of SPROUT++ in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge