A New Convergence Analysis of Plug-and-Play Proximal Gradient Descent Under Prior Mismatch

In this work, we provide a new convergence theory for plug-and-play proximal gradient descent (PnP-PGD) under prior mismatch where the denoiser is trained on a different data distribution to the inference task at hand. To the best of our knowledge, this is the first convergence proof of PnP-PGD under prior mismatch. Compared with the existing theoretical results for PnP algorithms, our new results removed the need for several restrictive and unverifiable assumptions.

The Practicality of Normalizing Flow Test-Time Training in Bayesian Inference for Agent-Based Models

Agent-Based Models (ABMs) are gaining great popularity in economics and social science because of their strong flexibility to describe the realistic and heterogeneous decisions and interaction rules between individual agents. In this work, we investigate for the first time the practicality of test-time training (TTT) of deep models such as normalizing flows, in the parameters posterior estimations of ABMs. We propose several practical TTT strategies for fine-tuning the normalizing flow against distribution shifts. Our numerical study demonstrates that TTT schemes are remarkably effective, enabling real-time adjustment of flow-based inference for ABM parameters.

Fast Equivariant Imaging: Acceleration for Unsupervised Learning via Augmented Lagrangian and Auxiliary PnP Denoisers

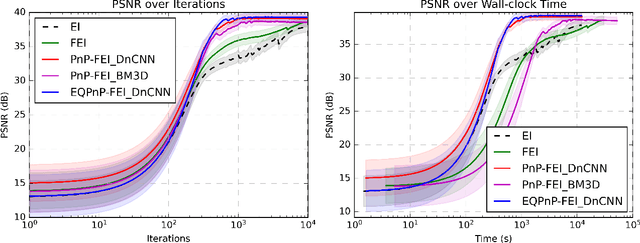
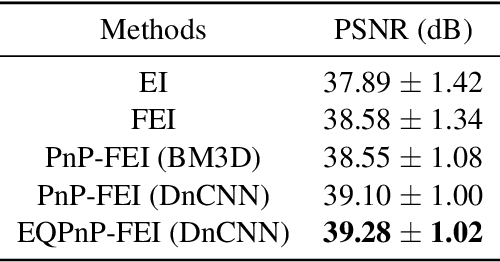
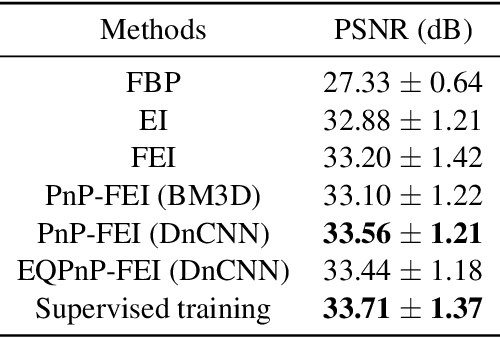
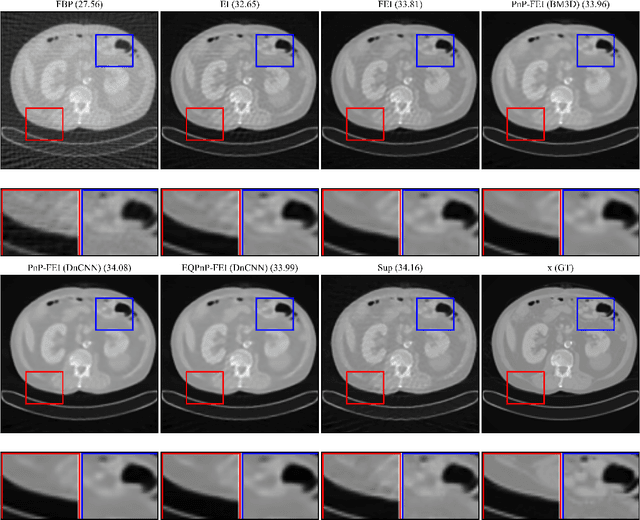
We propose Fast Equivariant Imaging (FEI), a novel unsupervised learning framework to efficiently train deep imaging networks without ground-truth data. From the perspective of reformulating the Equivariant Imaging based optimization problem via the method of Lagrange multipliers and utilizing plug-and-play denoisers, this novel unsupervised scheme shows superior efficiency and performance compared to vanilla Equivariant Imaging paradigm. In particular, our PnP-FEI scheme achieves an order-of-magnitude (10x) acceleration over standard EI on training U-Net with CT100 dataset for X-ray CT reconstruction, with improved generalization performance.

Sketched Equivariant Imaging Regularization and Deep Internal Learning for Inverse Problems

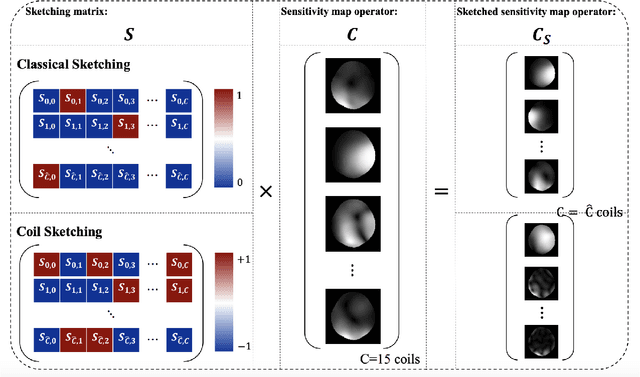
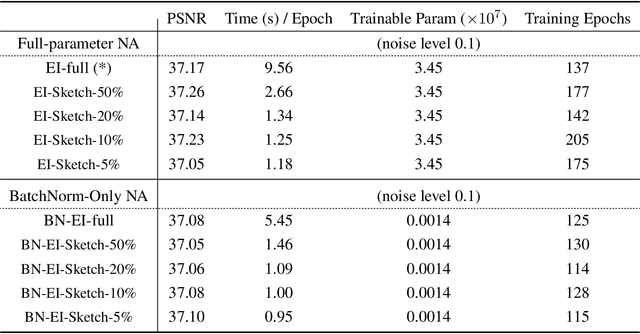
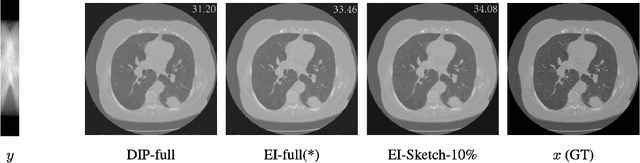
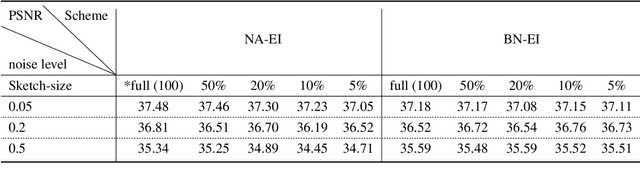
Equivariant Imaging (EI) regularization has become the de-facto technique for unsupervised training of deep imaging networks, without any need of ground-truth data. Observing that the EI-based unsupervised training paradigm currently has significant computational redundancy leading to inefficiency in high-dimensional applications, we propose a sketched EI regularization which leverages the randomized sketching techniques for acceleration. We then extend our sketched EI regularization to develop an accelerated deep internal learning framework -- Sketched Equivariant Deep Image Prior (Sk.EI-DIP), which can be efficiently applied for single-image and task-adapted reconstruction. Our numerical study on X-ray CT image reconstruction tasks demonstrate that our approach can achieve order-of-magnitude computational acceleration over standard EI-based counterpart in single-input setting, and network adaptation at test time.

On Estimating the Gradient of the Expected Information Gain in Bayesian Experimental Design

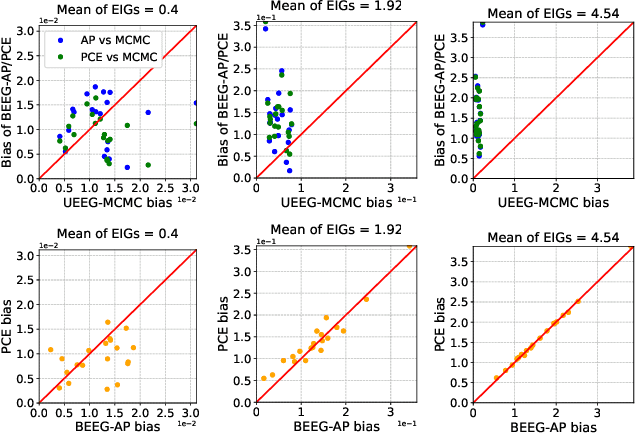
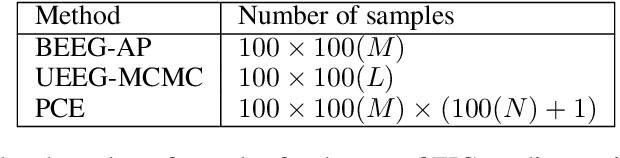
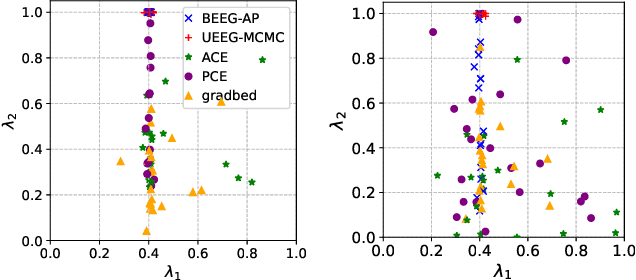
Bayesian Experimental Design (BED), which aims to find the optimal experimental conditions for Bayesian inference, is usually posed as to optimize the expected information gain (EIG). The gradient information is often needed for efficient EIG optimization, and as a result the ability to estimate the gradient of EIG is essential for BED problems. The primary goal of this work is to develop methods for estimating the gradient of EIG, which, combined with the stochastic gradient descent algorithms, result in efficient optimization of EIG. Specifically, we first introduce a posterior expected representation of the EIG gradient with respect to the design variables. Based on this, we propose two methods for estimating the EIG gradient, UEEG-MCMC that leverages posterior samples generated through Markov Chain Monte Carlo (MCMC) to estimate the EIG gradient, and BEEG-AP that focuses on achieving high simulation efficiency by repeatedly using parameter samples. Theoretical analysis and numerical studies illustrate that UEEG-MCMC is robust agains the actual EIG value, while BEEG-AP is more efficient when the EIG value to be optimized is small. Moreover, both methods show superior performance compared to several popular benchmarks in our numerical experiments.

Deep Unrolling Networks with Recurrent Momentum Acceleration for Nonlinear Inverse Problems

Combining the strengths of model-based iterative algorithms and data-driven deep learning solutions, deep unrolling networks (DuNets) have become a popular tool to solve inverse imaging problems. While DuNets have been successfully applied to many linear inverse problems, nonlinear problems tend to impair the performance of the method. Inspired by momentum acceleration techniques that are often used in optimization algorithms, we propose a recurrent momentum acceleration (RMA) framework that uses a long short-term memory recurrent neural network (LSTM-RNN) to simulate the momentum acceleration process. The RMA module leverages the ability of the LSTM-RNN to learn and retain knowledge from the previous gradients. We apply RMA to two popular DuNets -- the learned proximal gradient descent (LPGD) and the learned primal-dual (LPD) methods, resulting in LPGD-RMA and LPD-RMA respectively. We provide experimental results on two nonlinear inverse problems: a nonlinear deconvolution problem, and an electrical impedance tomography problem with limited boundary measurements. In the first experiment we have observed that the improvement due to RMA largely increases with respect to the nonlinearity of the problem. The results of the second example further demonstrate that the RMA schemes can significantly improve the performance of DuNets in strongly ill-posed problems.

NF-ULA: Langevin Monte Carlo with Normalizing Flow Prior for Imaging Inverse Problems

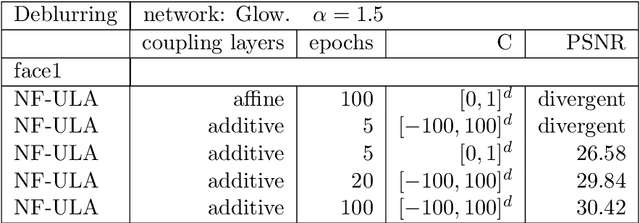
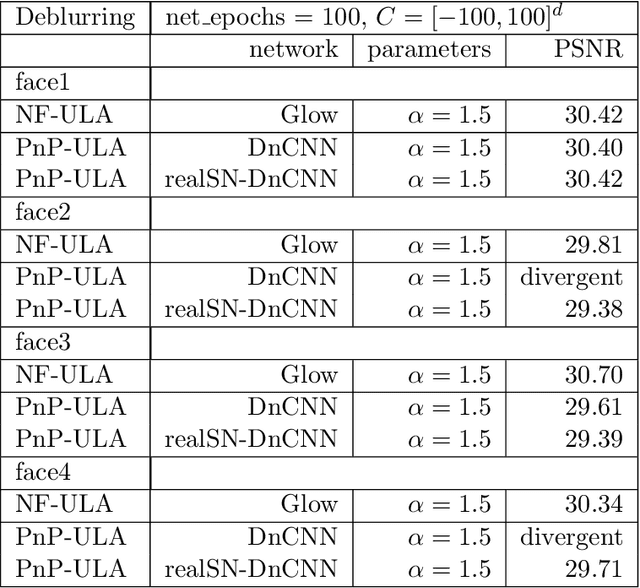
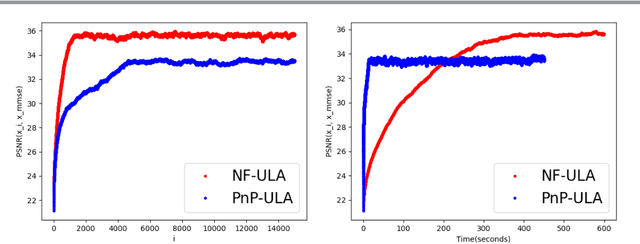
Bayesian methods for solving inverse problems are a powerful alternative to classical methods since the Bayesian approach gives a probabilistic description of the problems and offers the ability to quantify the uncertainty in the solution. Meanwhile, solving inverse problems by data-driven techniques also proves to be successful, due to the increasing representation ability of data-based models. In this work, we try to incorporate the data-based models into a class of Langevin-based sampling algorithms in Bayesian inference. Loosely speaking, we introduce NF-ULA (Unadjusted Langevin algorithms by Normalizing Flows), which involves learning a normalizing flow as the prior. In particular, our algorithm only requires a pre-trained normalizing flow, which is independent of the considered inverse problem and the forward operator. We perform theoretical analysis by investigating the well-posedness of the Bayesian solution and the non-asymptotic convergence of the NF-ULA algorithm. The efficacy of the proposed NF-ULA algorithm is demonstrated in various imaging problems, including image deblurring, image inpainting, and limited-angle X-ray computed tomography (CT) reconstruction.

VI-DGP: A variational inference method with deep generative prior for solving high-dimensional inverse problems

Solving high-dimensional Bayesian inverse problems (BIPs) with the variational inference (VI) method is promising but still challenging. The main difficulties arise from two aspects. First, VI methods approximate the posterior distribution using a simple and analytic variational distribution, which makes it difficult to estimate complex spatially-varying parameters in practice. Second, VI methods typically rely on gradient-based optimization, which can be computationally expensive or intractable when applied to BIPs involving partial differential equations (PDEs). To address these challenges, we propose a novel approximation method for estimating the high-dimensional posterior distribution. This approach leverages a deep generative model to learn a prior model capable of generating spatially-varying parameters. This enables posterior approximation over the latent variable instead of the complex parameters, thus improving estimation accuracy. Moreover, to accelerate gradient computation, we employ a differentiable physics-constrained surrogate model to replace the adjoint method. The proposed method can be fully implemented in an automatic differentiation manner. Numerical examples demonstrate two types of log-permeability estimation for flow in heterogeneous media. The results show the validity, accuracy, and high efficiency of the proposed method.

ODEs learn to walk: ODE-Net based data-driven modeling for crowd dynamics

Predicting the behaviors of pedestrian crowds is of critical importance for a variety of real-world problems. Data driven modeling, which aims to learn the mathematical models from observed data, is a promising tool to construct models that can make accurate predictions of such systems. In this work, we present a data-driven modeling approach based on the ODE-Net framework, for constructing continuous-time models of crowd dynamics. We discuss some challenging issues in applying the ODE-Net method to such problems, which are primarily associated with the dimensionality of the underlying crowd system, and we propose to address these issues by incorporating the social-force concept in the ODE-Net framework. Finally application examples are provided to demonstrate the performance of the proposed method.

Linear-Mapping based Variational Ensemble Kalman Filter

We propose a linear-mapping based variational Ensemble Kalman filter for sequential Bayesian filtering problems with generic observation models. Specifically, the proposed method is formulated as to construct a linear mapping from the prior ensemble to the posterior one, and the linear mapping is computed via a variational Bayesian formulation, i.e., by minimizing the Kullback-Leibler divergence between the transformed distribution by the linear mapping and the actual posterior. A gradient descent scheme is proposed to solve the resulting optimization problem. With numerical examples we demonstrate that the method has competitive performance against existing methods.