Dimension-reduced KRnet maps for high-dimensional Bayesian inverse problems

We present a dimension-reduced KRnet map approach (DR-KRnet) for high-dimensional Bayesian inverse problems, which is based on an explicit construction of a map that pushes forward the prior measure to the posterior measure in the latent space. Our approach consists of two main components: data-driven VAE prior and density approximation of the posterior of the latent variable. In reality, it may not be trivial to initialize a prior distribution that is consistent with available prior data; in other words, the complex prior information is often beyond simple hand-crafted priors. We employ variational autoencoder (VAE) to approximate the underlying distribution of the prior dataset, which is achieved through a latent variable and a decoder. Using the decoder provided by the VAE prior, we reformulate the problem in a low-dimensional latent space. In particular, we seek an invertible transport map given by KRnet to approximate the posterior distribution of the latent variable. Moreover, an efficient physics-constrained surrogate model without any labeled data is constructed to reduce the computational cost of solving both forward and adjoint problems involved in likelihood computation. With numerical experiments, we demonstrate the accuracy and efficiency of DR-KRnet for high-dimensional Bayesian inverse problems.

Streaming probabilistic tensor train decomposition

The Bayesian streaming tensor decomposition method is a novel method to discover the low-rank approximation of streaming data. However, when the streaming data comes from a high-order tensor, tensor structures of existing Bayesian streaming tensor decomposition algorithms may not be suitable in terms of representation and computation power. In this paper, we present a new Bayesian streaming tensor decomposition method based on tensor train (TT) decomposition. Especially, TT decomposition renders an efficient approach to represent high-order tensors. By exploiting the streaming variational inference (SVI) framework and TT decomposition, we can estimate the latent structure of high-order incomplete noisy streaming tensors. The experiments in synthetic and real-world data show the accuracy of our algorithm compared to the state-of-the-art Bayesian streaming tensor decomposition approaches.

VI-DGP: A variational inference method with deep generative prior for solving high-dimensional inverse problems

Solving high-dimensional Bayesian inverse problems (BIPs) with the variational inference (VI) method is promising but still challenging. The main difficulties arise from two aspects. First, VI methods approximate the posterior distribution using a simple and analytic variational distribution, which makes it difficult to estimate complex spatially-varying parameters in practice. Second, VI methods typically rely on gradient-based optimization, which can be computationally expensive or intractable when applied to BIPs involving partial differential equations (PDEs). To address these challenges, we propose a novel approximation method for estimating the high-dimensional posterior distribution. This approach leverages a deep generative model to learn a prior model capable of generating spatially-varying parameters. This enables posterior approximation over the latent variable instead of the complex parameters, thus improving estimation accuracy. Moreover, to accelerate gradient computation, we employ a differentiable physics-constrained surrogate model to replace the adjoint method. The proposed method can be fully implemented in an automatic differentiation manner. Numerical examples demonstrate two types of log-permeability estimation for flow in heterogeneous media. The results show the validity, accuracy, and high efficiency of the proposed method.

Deep neural network based adaptive learning for switched systems

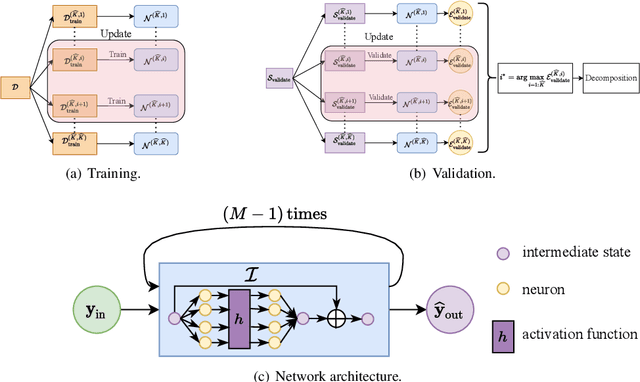
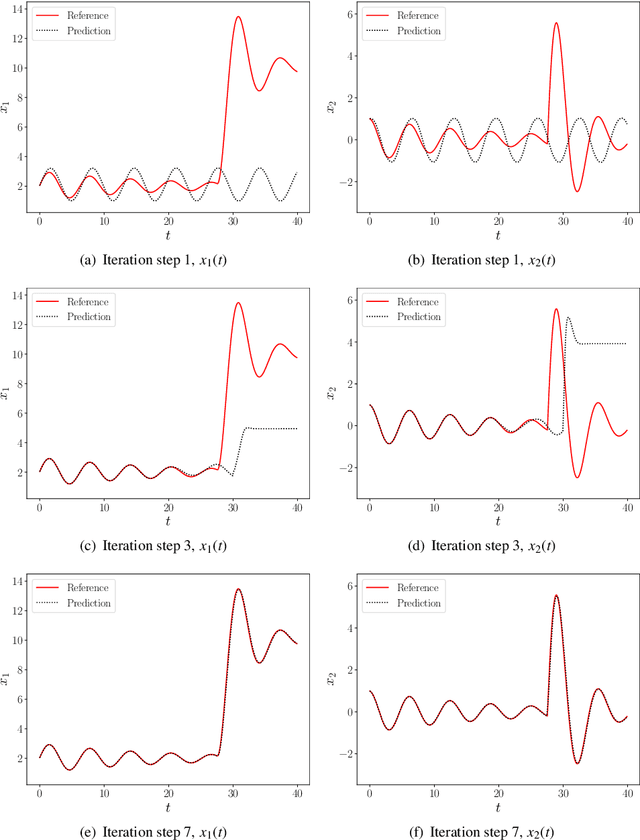
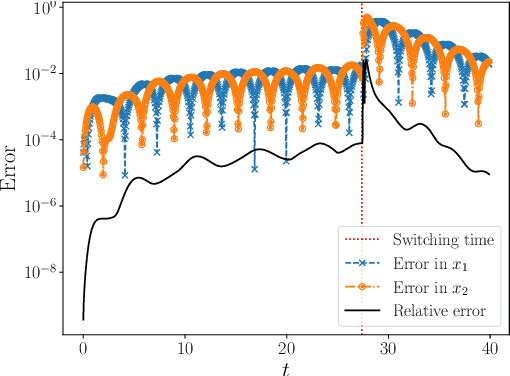
In this paper, we present a deep neural network based adaptive learning (DNN-AL) approach for switched systems. Currently, deep neural network based methods are actively developed for learning governing equations in unknown dynamic systems, but their efficiency can degenerate for switching systems, where structural changes exist at discrete time instants. In this new DNN-AL strategy, observed datasets are adaptively decomposed into subsets, such that no structural changes within each subset. During the adaptive procedures, DNNs are hierarchically constructed, and unknown switching time instants are gradually identified. Especially, network parameters at previous iteration steps are reused to initialize networks for the later iteration steps, which gives efficient training procedures for the DNNs. For the DNNs obtained through our DNN-AL, bounds of the prediction error are established. Numerical studies are conducted to demonstrate the efficiency of DNN-AL.

Adaptive deep density approximation for Fokker-Planck equations

In this paper we present a novel adaptive deep density approximation strategy based on KRnet (ADDA-KR) for solving the steady-state Fokker-Planck equation. It is known that this equation typically has high-dimensional spatial variables posed on unbounded domains, which limit the application of traditional grid based numerical methods. With the Knothe-Rosenblatt rearrangement, our newly proposed flow-based generative model, called KRnet, provides a family of probability density functions to serve as effective solution candidates of the Fokker-Planck equation, which have weaker dependence on dimensionality than traditional computational approaches. To result in effective stochastic collocation points for training KRnet, we develop an adaptive sampling procedure, where samples are generated iteratively using KRnet at each iteration. In addition, we give a detailed discussion of KRnet and show that it can efficiently estimate general high-dimensional density functions. We present a general mathematical framework of ADDA-KR, validate its accuracy and demonstrate its efficiency with numerical experiments.

Tensor Train Random Projection

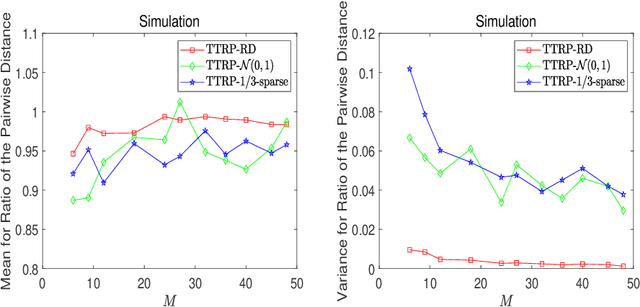
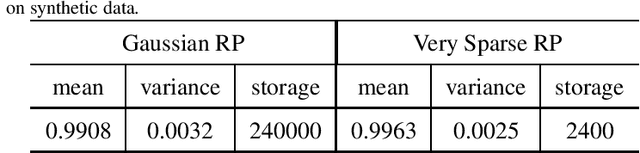
This work proposes a novel tensor train random projection (TTRP) method for dimension reduction, where the pairwise distances can be approximately preserved. Based on the tensor train format, this new random projection method can speed up the computation for high dimensional problems and requires less storage with little loss in accuracy, compared with existing methods (e.g., very sparse random projection). Our TTRP is systematically constructed through a rank-one TT-format with Rademacher random variables, which results in efficient projection with small variances. The isometry property of TTRP is proven in this work, and detailed numerical experiments with data sets (synthetic, MNIST and CIFAR-10) are conducted to demonstrate the efficiency of TTRP.

D3M: A deep domain decomposition method for partial differential equations

A state-of-the-art deep domain decomposition method (D3M) based on the variational principle is proposed for partial differential equations (PDEs). The solution of PDEs can be formulated as the solution of a constrained optimization problem, and we design a multi-fidelity neural network framework to solve this optimization problem. Our contribution is to develop a systematical computational procedure for the underlying problem in parallel with domain decomposition. Our analysis shows that the D3M approximation solution converges to the exact solution of underlying PDEs. Our proposed framework establishes a foundation to use variational deep learning in large-scale engineering problems and designs. We present a general mathematical framework of D3M, validate its accuracy and demonstrate its efficiency with numerical experiments.