Deep adaptive sampling for surrogate modeling without labeled data

Surrogate modeling is of great practical significance for parametric differential equation systems. In contrast to classical numerical methods, using physics-informed deep learning methods to construct simulators for such systems is a promising direction due to its potential to handle high dimensionality, which requires minimizing a loss over a training set of random samples. However, the random samples introduce statistical errors, which may become the dominant errors for the approximation of low-regularity and high-dimensional problems. In this work, we present a deep adaptive sampling method for surrogate modeling ($\text{DAS}^2$), where we generalize the deep adaptive sampling (DAS) method [62] [Tang, Wan and Yang, 2023] to build surrogate models for low-regularity parametric differential equations. In the parametric setting, the residual loss function can be regarded as an unnormalized probability density function (PDF) of the spatial and parametric variables. This PDF is approximated by a deep generative model, from which new samples are generated and added to the training set. Since the new samples match the residual-induced distribution, the refined training set can further reduce the statistical error in the current approximate solution. We demonstrate the effectiveness of $\text{DAS}^2$ with a series of numerical experiments, including the parametric lid-driven 2D cavity flow problem with a continuous range of Reynolds numbers from 100 to 1000.

Adversarial Adaptive Sampling: Unify PINN and Optimal Transport for the Approximation of PDEs

Solving partial differential equations (PDEs) is a central task in scientific computing. Recently, neural network approximation of PDEs has received increasing attention due to its flexible meshless discretization and its potential for high-dimensional problems. One fundamental numerical difficulty is that random samples in the training set introduce statistical errors into the discretization of loss functional which may become the dominant error in the final approximation, and therefore overshadow the modeling capability of the neural network. In this work, we propose a new minmax formulation to optimize simultaneously the approximate solution, given by a neural network model, and the random samples in the training set, provided by a deep generative model. The key idea is to use a deep generative model to adjust random samples in the training set such that the residual induced by the approximate PDE solution can maintain a smooth profile when it is being minimized. Such an idea is achieved by implicitly embedding the Wasserstein distance between the residual-induced distribution and the uniform distribution into the loss, which is then minimized together with the residual. A nearly uniform residual profile means that its variance is small for any normalized weight function such that the Monte Carlo approximation error of the loss functional is reduced significantly for a certain sample size. The adversarial adaptive sampling (AAS) approach proposed in this work is the first attempt to formulate two essential components, minimizing the residual and seeking the optimal training set, into one minmax objective functional for the neural network approximation of PDEs.

Dimension-reduced KRnet maps for high-dimensional Bayesian inverse problems

We present a dimension-reduced KRnet map approach (DR-KRnet) for high-dimensional Bayesian inverse problems, which is based on an explicit construction of a map that pushes forward the prior measure to the posterior measure in the latent space. Our approach consists of two main components: data-driven VAE prior and density approximation of the posterior of the latent variable. In reality, it may not be trivial to initialize a prior distribution that is consistent with available prior data; in other words, the complex prior information is often beyond simple hand-crafted priors. We employ variational autoencoder (VAE) to approximate the underlying distribution of the prior dataset, which is achieved through a latent variable and a decoder. Using the decoder provided by the VAE prior, we reformulate the problem in a low-dimensional latent space. In particular, we seek an invertible transport map given by KRnet to approximate the posterior distribution of the latent variable. Moreover, an efficient physics-constrained surrogate model without any labeled data is constructed to reduce the computational cost of solving both forward and adjoint problems involved in likelihood computation. With numerical experiments, we demonstrate the accuracy and efficiency of DR-KRnet for high-dimensional Bayesian inverse problems.

DAS: A deep adaptive sampling method for solving partial differential equations

In this work we propose a deep adaptive sampling (DAS) method for solving partial differential equations (PDEs), where deep neural networks are utilized to approximate the solutions of PDEs and deep generative models are employed to generate new collocation points that refine the training set. The overall procedure of DAS consists of two components: solving the PDEs by minimizing the residual loss on the collocation points in the training set and generating a new training set to further improve the accuracy of current approximate solution. In particular, we treat the residual as a probability density function and approximate it with a deep generative model, called KRnet. The new samples from KRnet are consistent with the distribution induced by the residual, i.e., more samples are located in the region of large residual and less samples are located in the region of small residual. Analogous to classical adaptive methods such as the adaptive finite element, KRnet acts as an error indicator that guides the refinement of the training set. Compared to the neural network approximation obtained with uniformly distributed collocation points, the developed algorithms can significantly improve the accuracy, especially for low regularity and high-dimensional problems. We present a theoretical analysis to show that the proposed DAS method can reduce the error bound and demonstrate its effectiveness with numerical experiments.

Augmented KRnet for density estimation and approximation

In this work, we have proposed augmented KRnets including both discrete and continuous models. One difficulty in flow-based generative modeling is to maintain the invertibility of the transport map, which is often a trade-off between effectiveness and robustness. The exact invertibility has been achieved in the real NVP using a specific pattern to exchange information between two separated groups of dimensions. KRnet has been developed to enhance the information exchange among data dimensions by incorporating the Knothe-Rosenblatt rearrangement into the structure of the transport map. Due to the maintenance of exact invertibility, a full nonlinear update of all data dimensions needs three iterations in KRnet. To alleviate this issue, we will add augmented dimensions that act as a channel for communications among the data dimensions. In the augmented KRnet, a fully nonlinear update is achieved in two iterations. We also show that the augmented KRnet can be reformulated as the discretization of a neural ODE, where the exact invertibility is kept such that the adjoint method can be formulated with respect to the discretized ODE to obtain the exact gradient. Numerical experiments have been implemented to demonstrate the effectiveness of our models.

Adaptive deep density approximation for Fokker-Planck equations

In this paper we present a novel adaptive deep density approximation strategy based on KRnet (ADDA-KR) for solving the steady-state Fokker-Planck equation. It is known that this equation typically has high-dimensional spatial variables posed on unbounded domains, which limit the application of traditional grid based numerical methods. With the Knothe-Rosenblatt rearrangement, our newly proposed flow-based generative model, called KRnet, provides a family of probability density functions to serve as effective solution candidates of the Fokker-Planck equation, which have weaker dependence on dimensionality than traditional computational approaches. To result in effective stochastic collocation points for training KRnet, we develop an adaptive sampling procedure, where samples are generated iteratively using KRnet at each iteration. In addition, we give a detailed discussion of KRnet and show that it can efficiently estimate general high-dimensional density functions. We present a general mathematical framework of ADDA-KR, validate its accuracy and demonstrate its efficiency with numerical experiments.

Tensor Train Random Projection

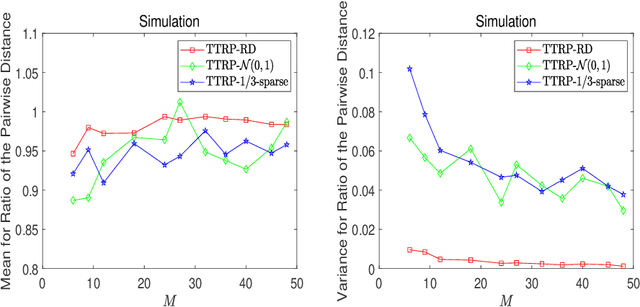
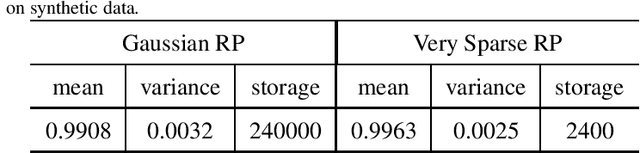
This work proposes a novel tensor train random projection (TTRP) method for dimension reduction, where the pairwise distances can be approximately preserved. Based on the tensor train format, this new random projection method can speed up the computation for high dimensional problems and requires less storage with little loss in accuracy, compared with existing methods (e.g., very sparse random projection). Our TTRP is systematically constructed through a rank-one TT-format with Rademacher random variables, which results in efficient projection with small variances. The isometry property of TTRP is proven in this work, and detailed numerical experiments with data sets (synthetic, MNIST and CIFAR-10) are conducted to demonstrate the efficiency of TTRP.

D3M: A deep domain decomposition method for partial differential equations

A state-of-the-art deep domain decomposition method (D3M) based on the variational principle is proposed for partial differential equations (PDEs). The solution of PDEs can be formulated as the solution of a constrained optimization problem, and we design a multi-fidelity neural network framework to solve this optimization problem. Our contribution is to develop a systematical computational procedure for the underlying problem in parallel with domain decomposition. Our analysis shows that the D3M approximation solution converges to the exact solution of underlying PDEs. Our proposed framework establishes a foundation to use variational deep learning in large-scale engineering problems and designs. We present a general mathematical framework of D3M, validate its accuracy and demonstrate its efficiency with numerical experiments.