Deep Learning Method for Computing Committor Functions with Adaptive Sampling

The committor function is a central object for quantifying the transitions between metastable states of dynamical systems. Recently, a number of computational methods based on deep neural networks have been developed for computing the high-dimensional committor function. The success of the methods relies on sampling adequate data for the transition, which still is a challenging task for complex systems at low temperatures. In this work, we propose a deep learning method with two novel adaptive sampling schemes (I and II). In the two schemes, the data are generated actively with a modified potential where the bias potential is constructed from the learned committor function. We theoretically demonstrate the advantages of the sampling schemes and show that the data in sampling scheme II are uniformly distributed along the transition tube. This makes a promising method for studying the transition of complex systems. The efficiency of the method is illustrated in high-dimensional systems including the alanine dipeptide and a solvated dimer system.

Computing Transition Pathways for the Study of Rare Events Using Deep Reinforcement Learning

Understanding the transition events between metastable states in complex systems is an important subject in the fields of computational physics, chemistry and biology. The transition pathway plays an important role in characterizing the mechanism underlying the transition, for example, in the study of conformational changes of bio-molecules. In fact, computing the transition pathway is a challenging task for complex and high-dimensional systems. In this work, we formulate the path-finding task as a cost minimization problem over a particular path space. The cost function is adapted from the Freidlin-Wentzell action functional so that it is able to deal with rough potential landscapes. The path-finding problem is then solved using a actor-critic method based on the deep deterministic policy gradient algorithm (DDPG). The method incorporates the potential force of the system in the policy for generating episodes and combines physical properties of the system with the learning process for molecular systems. The exploitation and exploration nature of reinforcement learning enables the method to efficiently sample the transition events and compute the globally optimal transition pathway. We illustrate the effectiveness of the proposed method using three benchmark systems including an extended Mueller system and the Lennard-Jones system of seven particles.

A Survey on Collaborative DNN Inference for Edge Intelligence

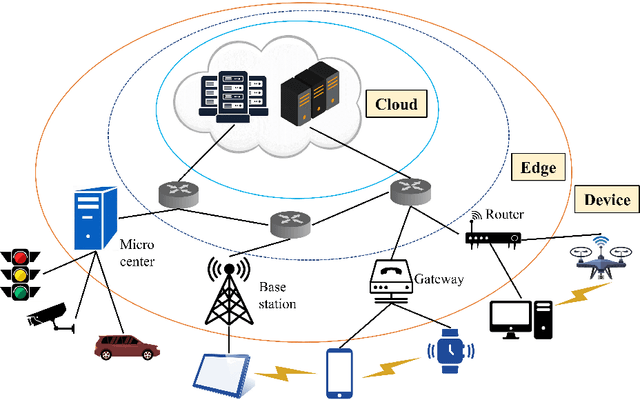
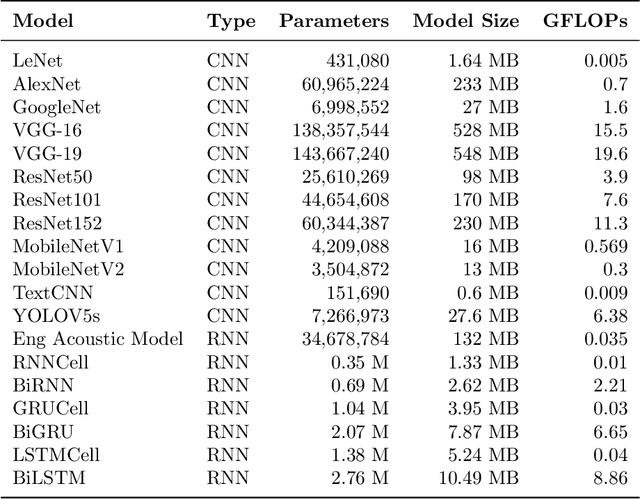
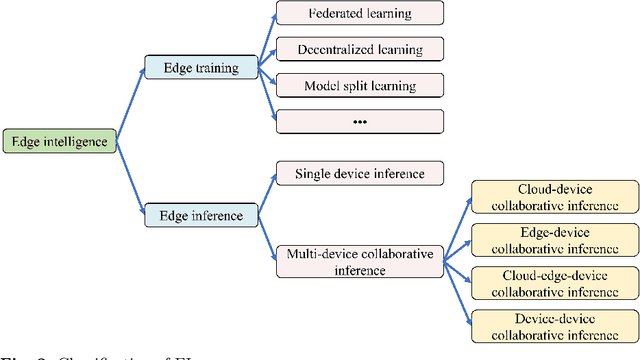
With the vigorous development of artificial intelligence (AI), the intelligent applications based on deep neural network (DNN) change people's lifestyles and the production efficiency. However, the huge amount of computation and data generated from the network edge becomes the major bottleneck, and traditional cloud-based computing mode has been unable to meet the requirements of real-time processing tasks. To solve the above problems, by embedding AI model training and inference capabilities into the network edge, edge intelligence (EI) becomes a cutting-edge direction in the field of AI. Furthermore, collaborative DNN inference among the cloud, edge, and end device provides a promising way to boost the EI. Nevertheless, at present, EI oriented collaborative DNN inference is still in its early stage, lacking a systematic classification and discussion of existing research efforts. Thus motivated, we have made a comprehensive investigation on the recent studies about EI oriented collaborative DNN inference. In this paper, we firstly review the background and motivation of EI. Then, we classify four typical collaborative DNN inference paradigms for EI, and analyze the characteristics and key technologies of them. Finally, we summarize the current challenges of collaborative DNN inference, discuss the future development trend and provide the future research direction.

Computing the Invariant Distribution of Randomly Perturbed Dynamical Systems Using Deep Learning

The invariant distribution, which is characterized by the stationary Fokker-Planck equation, is an important object in the study of randomly perturbed dynamical systems. Traditional numerical methods for computing the invariant distribution based on the Fokker-Planck equation, such as finite difference or finite element methods, are limited to low-dimensional systems due to the curse of dimensionality. In this work, we propose a deep learning based method to compute the generalized potential, i.e. the negative logarithm of the invariant distribution multiplied by the noise. The idea of the method is to learn a decomposition of the force field, as specified by the Fokker-Planck equation, from the trajectory data. The potential component of the decomposition gives the generalized potential. The method can deal with high-dimensional systems, possibly with partially known dynamics. Using the generalized potential also allows us to deal with systems at low temperatures, where the invariant distribution becomes singular around the metastable states. These advantages make it an efficient method to analyze invariant distributions for practical dynamical systems. The effectiveness of the proposed method is demonstrated by numerical examples.

A Data Driven Method for Computing Quasipotentials

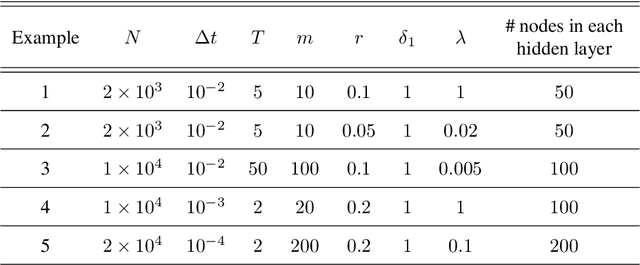
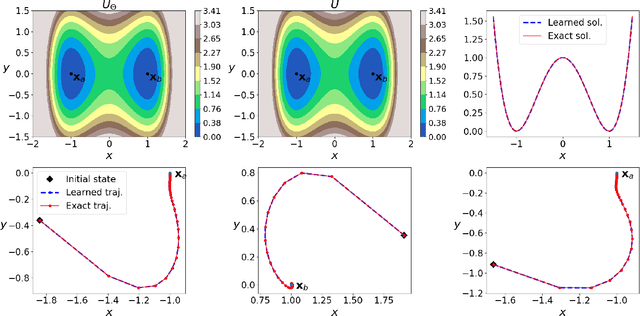
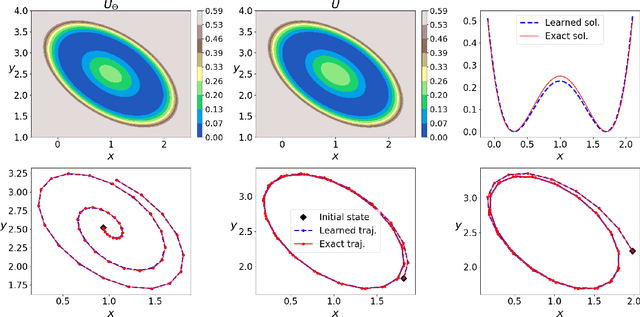
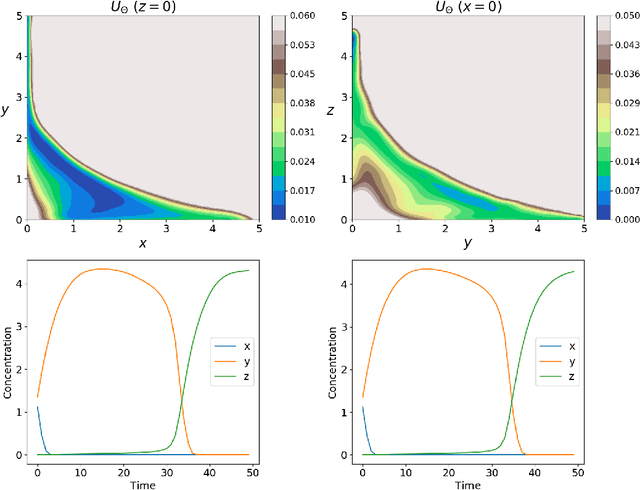
The quasipotential is a natural generalization of the concept of energy functions to non-equilibrium systems. In the analysis of rare events in stochastic dynamics, it plays a central role in characterizing the statistics of transition events and the likely transition paths. However, computing the quasipotential is challenging, especially in high dimensional dynamical systems where a global landscape is sought. Traditional methods based on the dynamic programming principle or path space minimization tend to suffer from the curse of dimensionality. In this paper, we propose a simple and efficient machine learning method to resolve this problem. The key idea is to learn an orthogonal decomposition of the vector field that drives the dynamics, from which one can identify the quasipotential. We demonstrate on various example systems that our method can effectively compute quasipotential landscapes without requiring spatial discretization or solving path-space optimization problems. Moreover, the method is purely data driven in the sense that only observed trajectories of the dynamics are required for the computation of the quasipotential. These properties make it a promising method to enable the general application of quasipotential analysis to dynamical systems away from equilibrium.

Computing Committor Functions for the Study of Rare Events Using Deep Learning

The committor function is a central object of study in understanding transitions between metastable states in complex systems. However, computing the committor function for realistic systems at low temperatures is a challenging task, due to the curse of dimensionality and the scarcity of transition data. In this paper, we introduce a computational approach that overcomes these issues and achieves good performance on complex benchmark problems with rough energy landscapes. The new approach combines deep learning, data sampling and feature engineering techniques. This establishes an alternative practical method for studying rare transition events between metastable states in complex, high dimensional systems.