A Data Driven Method for Computing Quasipotentials
Paper and Code
Dec 13, 2020
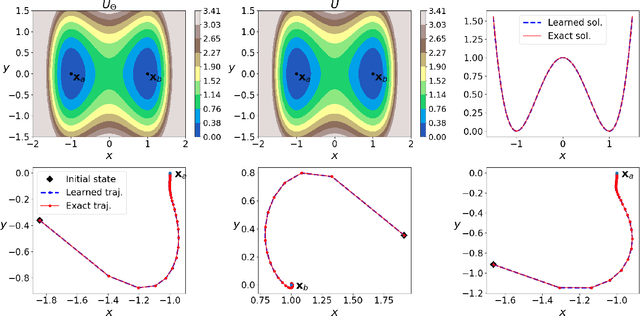
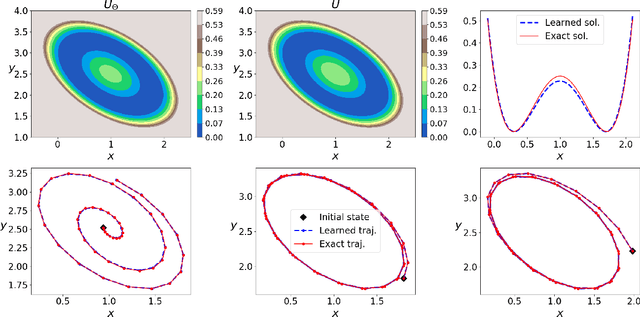
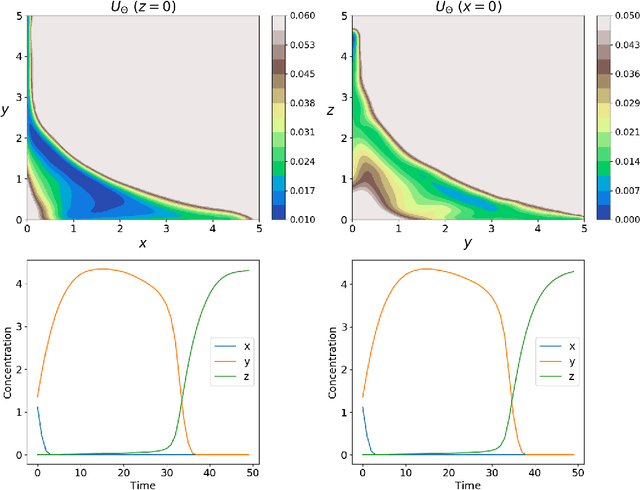
The quasipotential is a natural generalization of the concept of energy functions to non-equilibrium systems. In the analysis of rare events in stochastic dynamics, it plays a central role in characterizing the statistics of transition events and the likely transition paths. However, computing the quasipotential is challenging, especially in high dimensional dynamical systems where a global landscape is sought. Traditional methods based on the dynamic programming principle or path space minimization tend to suffer from the curse of dimensionality. In this paper, we propose a simple and efficient machine learning method to resolve this problem. The key idea is to learn an orthogonal decomposition of the vector field that drives the dynamics, from which one can identify the quasipotential. We demonstrate on various example systems that our method can effectively compute quasipotential landscapes without requiring spatial discretization or solving path-space optimization problems. Moreover, the method is purely data driven in the sense that only observed trajectories of the dynamics are required for the computation of the quasipotential. These properties make it a promising method to enable the general application of quasipotential analysis to dynamical systems away from equilibrium.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge