Numerical Investigation of Sequence Modeling Theory using Controllable Memory Functions

The evolution of sequence modeling architectures, from recurrent neural networks and convolutional models to Transformers and structured state-space models, reflects ongoing efforts to address the diverse temporal dependencies inherent in sequential data. Despite this progress, systematically characterizing the strengths and limitations of these architectures remains a fundamental challenge.In this work, we propose a synthetic benchmarking framework to evaluate how effectively different sequence models capture distinct temporal structures. The core of this approach is to generate synthetic targets, each characterized by a memory function and a parameter that determines the strength of temporal dependence. This setup allows us to produce a continuum of tasks that vary in temporal complexity, enabling fine-grained analysis of model behavior concerning specific memory properties. We focus on four representative memory functions, each corresponding to a distinct class of temporal structures.Experiments on several sequence modeling architectures confirm existing theoretical insights and reveal new findings.These results demonstrate the effectiveness of the proposed method in advancing theoretical understandingand highlight the importance of using controllable targets with clearly defined structures for evaluating sequence modeling architectures.

Learning task-specific predictive models for scientific computing

We consider learning a predictive model to be subsequently used for a given downstream task (described by an algorithm) that requires access to the model evaluation. This task need not be prediction, and this situation is frequently encountered in machine-learning-augmented scientific computing. We show that this setting differs from classical supervised learning, and in general it cannot be solved by minimizing the mean square error of the model predictions as is frequently performed in the literature. Instead, we find that the maximum prediction error on the support of the downstream task algorithm can serve as an effective estimate for the subsequent task performance. With this insight, we formulate a task-specific supervised learning problem based on the given sampling measure, whose solution serves as a reliable surrogate model for the downstream task. Then, we discretize the empirical risk based on training data, and develop an iterative algorithm to solve the task-specific supervised learning problem. Three illustrative numerical examples on trajectory prediction, optimal control and minimum energy path computation demonstrate the effectiveness of the approach.

Continuity-Preserving Convolutional Autoencoders for Learning Continuous Latent Dynamical Models from Images

Continuous dynamical systems are cornerstones of many scientific and engineering disciplines. While machine learning offers powerful tools to model these systems from trajectory data, challenges arise when these trajectories are captured as images, resulting in pixel-level observations that are discrete in nature. Consequently, a naive application of a convolutional autoencoder can result in latent coordinates that are discontinuous in time. To resolve this, we propose continuity-preserving convolutional autoencoders (CpAEs) to learn continuous latent states and their corresponding continuous latent dynamical models from discrete image frames. We present a mathematical formulation for learning dynamics from image frames, which illustrates issues with previous approaches and motivates our methodology based on promoting the continuity of convolution filters, thereby preserving the continuity of the latent states. This approach enables CpAEs to produce latent states that evolve continuously with the underlying dynamics, leading to more accurate latent dynamical models. Extensive experiments across various scenarios demonstrate the effectiveness of CpAEs.

Autocorrelation Matters: Understanding the Role of Initialization Schemes for State Space Models

Current methods for initializing state space model (SSM) parameters primarily rely on the HiPPO framework \citep{gu2023how}, which is based on online function approximation with the SSM kernel basis. However, the HiPPO framework does not explicitly account for the effects of the temporal structures of input sequences on the optimization of SSMs. In this paper, we take a further step to investigate the roles of SSM initialization schemes by considering the autocorrelation of input sequences. Specifically, we: (1) rigorously characterize the dependency of the SSM timescale on sequence length based on sequence autocorrelation; (2) find that with a proper timescale, allowing a zero real part for the eigenvalues of the SSM state matrix mitigates the curse of memory while still maintaining stability at initialization; (3) show that the imaginary part of the eigenvalues of the SSM state matrix determines the conditioning of SSM optimization problems, and uncover an approximation-estimation tradeoff when training SSMs with a specific class of target functions.

Learning Macroscopic Dynamics from Partial Microscopic Observations

Macroscopic observables of a system are of keen interest in real applications such as the design of novel materials. Current methods rely on microscopic trajectory simulations, where the forces on all microscopic coordinates need to be computed or measured. However, this can be computationally prohibitive for realistic systems. In this paper, we propose a method to learn macroscopic dynamics requiring only force computations on a subset of the microscopic coordinates. Our method relies on a sparsity assumption: the force on each microscopic coordinate relies only on a small number of other coordinates. The main idea of our approach is to map the training procedure on the macroscopic coordinates back to the microscopic coordinates, on which partial force computations can be used as stochastic estimation to update model parameters. We provide a theoretical justification of this under suitable conditions. We demonstrate the accuracy, force computation efficiency, and robustness of our method on learning macroscopic closure models from a variety of microscopic systems, including those modeled by partial differential equations or molecular dynamics simulations.

Unifying back-propagation and forward-forward algorithms through model predictive control

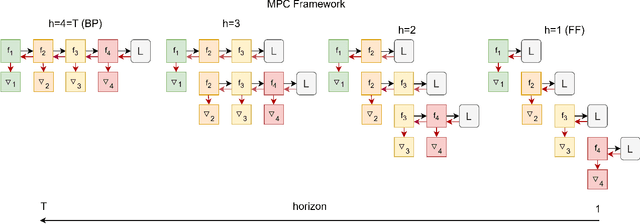
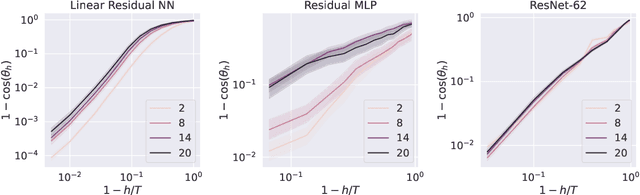
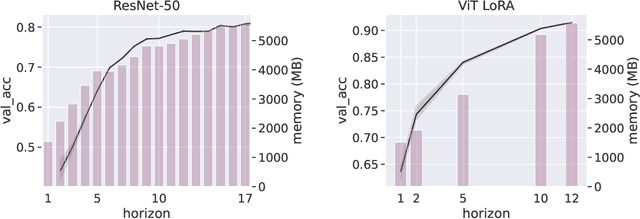
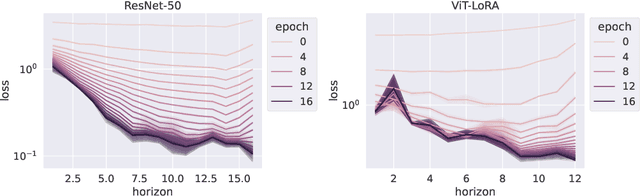
We introduce a Model Predictive Control (MPC) framework for training deep neural networks, systematically unifying the Back-Propagation (BP) and Forward-Forward (FF) algorithms. At the same time, it gives rise to a range of intermediate training algorithms with varying look-forward horizons, leading to a performance-efficiency trade-off. We perform a precise analysis of this trade-off on a deep linear network, where the qualitative conclusions carry over to general networks. Based on our analysis, we propose a principled method to choose the optimization horizon based on given objectives and model specifications. Numerical results on various models and tasks demonstrate the versatility of our method.

Accelerating Legacy Numerical Solvers by Non-intrusive Gradient-based Meta-solving

Scientific computing is an essential tool for scientific discovery and engineering design, and its computational cost is always a main concern in practice. To accelerate scientific computing, it is a promising approach to use machine learning (especially meta-learning) techniques for selecting hyperparameters of traditional numerical methods. There have been numerous proposals to this direction, but many of them require automatic-differentiable numerical methods. However, in reality, many practical applications still depend on well-established but non-automatic-differentiable legacy codes, which prevents practitioners from applying the state-of-the-art research to their own problems. To resolve this problem, we propose a non-intrusive methodology with a novel gradient estimation technique to combine machine learning and legacy numerical codes without any modification. We theoretically and numerically show the advantage of the proposed method over other baselines and present applications of accelerating established non-automatic-differentiable numerical solvers implemented in PETSc, a widely used open-source numerical software library.

From Generalization Analysis to Optimization Designs for State Space Models

A State Space Model (SSM) is a foundation model in time series analysis, which has recently been shown as an alternative to transformers in sequence modeling. In this paper, we theoretically study the generalization of SSMs and propose improvements to training algorithms based on the generalization results. Specifically, we give a \textit{data-dependent} generalization bound for SSMs, showing an interplay between the SSM parameters and the temporal dependencies of the training sequences. Leveraging the generalization bound, we (1) set up a scaling rule for model initialization based on the proposed generalization measure, which significantly improves the robustness of the output value scales on SSMs to different temporal patterns in the sequence data; (2) introduce a new regularization method for training SSMs to enhance the generalization performance. Numerical results are conducted to validate our results.

PID Control-Based Self-Healing to Improve the Robustness of Large Language Models

Despite the effectiveness of deep neural networks in numerous natural language processing applications, recent findings have exposed the vulnerability of these language models when minor perturbations are introduced. While appearing semantically indistinguishable to humans, these perturbations can significantly reduce the performance of well-trained language models, raising concerns about the reliability of deploying them in safe-critical situations. In this work, we construct a computationally efficient self-healing process to correct undesired model behavior during online inference when perturbations are applied to input data. This is formulated as a trajectory optimization problem in which the internal states of the neural network layers are automatically corrected using a PID (Proportional-Integral-Derivative) control mechanism. The P controller targets immediate state adjustments, while the I and D controllers consider past states and future dynamical trends, respectively. We leverage the geometrical properties of the training data to design effective linear PID controllers. This approach reduces the computational cost to that of using just the P controller, instead of the full PID control. Further, we introduce an analytical method for approximating the optimal control solutions, enhancing the real-time inference capabilities of this controlled system. Moreover, we conduct a theoretical error analysis of the analytic solution in a simplified setting. The proposed PID control-based self-healing is a low cost framework that improves the robustness of pre-trained large language models, whether standard or robustly trained, against a wide range of perturbations. A detailed implementation can be found in:https://github.com/zhuotongchen/PID-Control-Based-Self-Healing-to-Improve-the-Robustness-of-Large-Language-Models.

DynGMA: a robust approach for learning stochastic differential equations from data

Learning unknown stochastic differential equations (SDEs) from observed data is a significant and challenging task with applications in various fields. Current approaches often use neural networks to represent drift and diffusion functions, and construct likelihood-based loss by approximating the transition density to train these networks. However, these methods often rely on one-step stochastic numerical schemes, necessitating data with sufficiently high time resolution. In this paper, we introduce novel approximations to the transition density of the parameterized SDE: a Gaussian density approximation inspired by the random perturbation theory of dynamical systems, and its extension, the dynamical Gaussian mixture approximation (DynGMA). Benefiting from the robust density approximation, our method exhibits superior accuracy compared to baseline methods in learning the fully unknown drift and diffusion functions and computing the invariant distribution from trajectory data. And it is capable of handling trajectory data with low time resolution and variable, even uncontrollable, time step sizes, such as data generated from Gillespie's stochastic simulations. We then conduct several experiments across various scenarios to verify the advantages and robustness of the proposed method.