Paid with Models: Optimal Contract Design for Collaborative Machine Learning

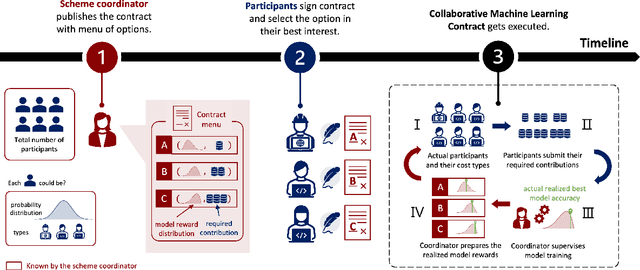
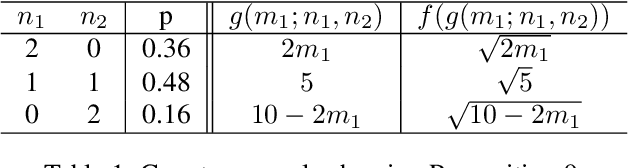
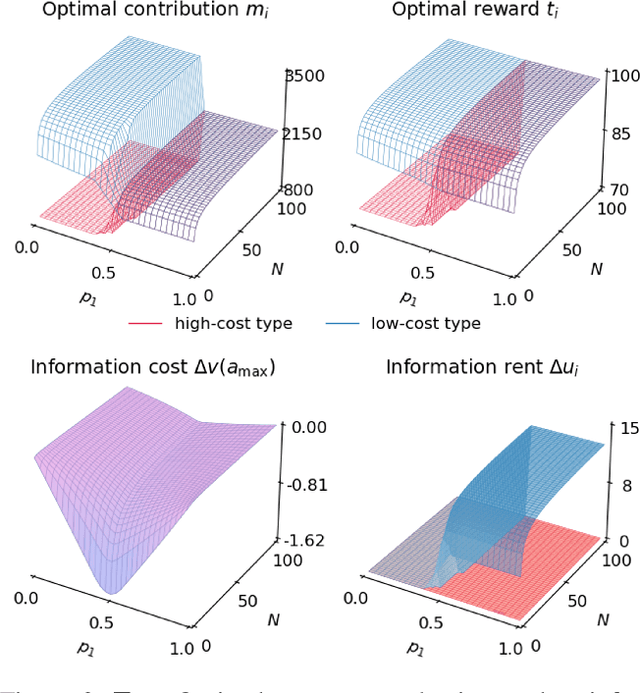
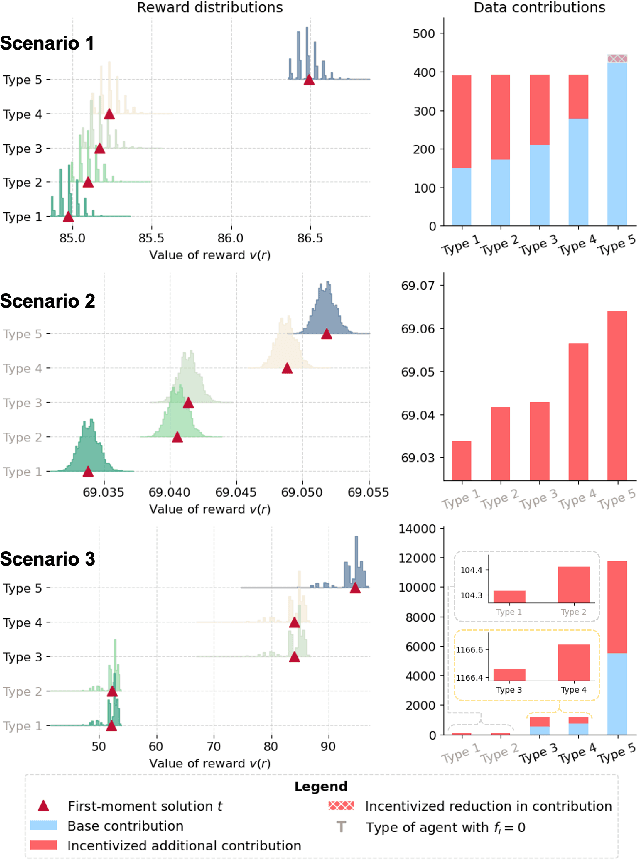
Collaborative machine learning (CML) provides a promising paradigm for democratizing advanced technologies by enabling cost-sharing among participants. However, the potential for rent-seeking behaviors among parties can undermine such collaborations. Contract theory presents a viable solution by rewarding participants with models of varying accuracy based on their contributions. However, unlike monetary compensation, using models as rewards introduces unique challenges, particularly due to the stochastic nature of these rewards when contribution costs are privately held information. This paper formalizes the optimal contracting problem within CML and proposes a transformation that simplifies the non-convex optimization problem into one that can be solved through convex optimization algorithms. We conduct a detailed analysis of the properties that an optimal contract must satisfy when models serve as the rewards, and we explore the potential benefits and welfare implications of these contract-driven CML schemes through numerical experiments.

Autocorrelation Matters: Understanding the Role of Initialization Schemes for State Space Models

Current methods for initializing state space model (SSM) parameters primarily rely on the HiPPO framework \citep{gu2023how}, which is based on online function approximation with the SSM kernel basis. However, the HiPPO framework does not explicitly account for the effects of the temporal structures of input sequences on the optimization of SSMs. In this paper, we take a further step to investigate the roles of SSM initialization schemes by considering the autocorrelation of input sequences. Specifically, we: (1) rigorously characterize the dependency of the SSM timescale on sequence length based on sequence autocorrelation; (2) find that with a proper timescale, allowing a zero real part for the eigenvalues of the SSM state matrix mitigates the curse of memory while still maintaining stability at initialization; (3) show that the imaginary part of the eigenvalues of the SSM state matrix determines the conditioning of SSM optimization problems, and uncover an approximation-estimation tradeoff when training SSMs with a specific class of target functions.

Cross-Domain Feature Augmentation for Domain Generalization

Domain generalization aims to develop models that are robust to distribution shifts. Existing methods focus on learning invariance across domains to enhance model robustness, and data augmentation has been widely used to learn invariant predictors, with most methods performing augmentation in the input space. However, augmentation in the input space has limited diversity whereas in the feature space is more versatile and has shown promising results. Nonetheless, feature semantics is seldom considered and existing feature augmentation methods suffer from a limited variety of augmented features. We decompose features into class-generic, class-specific, domain-generic, and domain-specific components. We propose a cross-domain feature augmentation method named XDomainMix that enables us to increase sample diversity while emphasizing the learning of invariant representations to achieve domain generalization. Experiments on widely used benchmark datasets demonstrate that our proposed method is able to achieve state-of-the-art performance. Quantitative analysis indicates that our feature augmentation approach facilitates the learning of effective models that are invariant across different domains.

From Generalization Analysis to Optimization Designs for State Space Models

A State Space Model (SSM) is a foundation model in time series analysis, which has recently been shown as an alternative to transformers in sequence modeling. In this paper, we theoretically study the generalization of SSMs and propose improvements to training algorithms based on the generalization results. Specifically, we give a \textit{data-dependent} generalization bound for SSMs, showing an interplay between the SSM parameters and the temporal dependencies of the training sequences. Leveraging the generalization bound, we (1) set up a scaling rule for model initialization based on the proposed generalization measure, which significantly improves the robustness of the output value scales on SSMs to different temporal patterns in the sequence data; (2) introduce a new regularization method for training SSMs to enhance the generalization performance. Numerical results are conducted to validate our results.

Data-Free Diversity-Based Ensemble Selection For One-Shot Federated Learning in Machine Learning Model Market

The emerging availability of trained machine learning models has put forward the novel concept of Machine Learning Model Market in which one can harness the collective intelligence of multiple well-trained models to improve the performance of the resultant model through one-shot federated learning and ensemble learning in a data-free manner. However, picking the models available in the market for ensemble learning is time-consuming, as using all the models is not always the best approach. It is thus crucial to have an effective ensemble selection strategy that can find a good subset of the base models for the ensemble. Conventional ensemble selection techniques are not applicable, as we do not have access to the local datasets of the parties in the federated learning setting. In this paper, we present a novel Data-Free Diversity-Based method called DeDES to address the ensemble selection problem for models generated by one-shot federated learning in practical applications such as model markets. Experiments showed that our method can achieve both better performance and higher efficiency over 5 datasets and 4 different model structures under the different data-partition strategies.

Connecting Optimization and Generalization via Gradient Flow Path Length

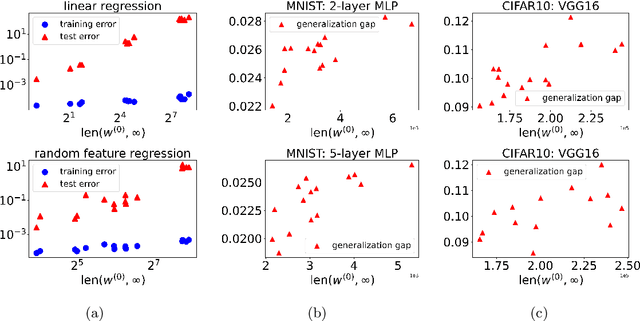
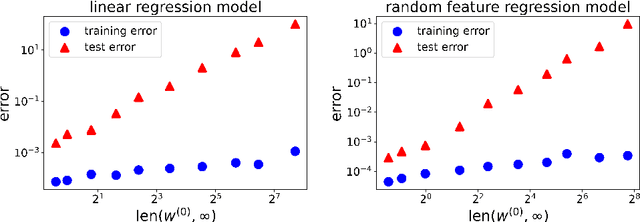
Optimization and generalization are two essential aspects of machine learning. In this paper, we propose a framework to connect optimization with generalization by analyzing the generalization error based on the length of optimization trajectory under the gradient flow algorithm after convergence. Through our approach, we show that, with a proper initialization, gradient flow converges following a short path with an explicit length estimate. Such an estimate induces a length-based generalization bound, showing that short optimization paths after convergence are associated with good generalization, which also matches our numerical results. Our framework can be applied to broad settings. For example, we use it to obtain generalization estimates on three distinct machine learning models: underdetermined $\ell_p$ linear regression, kernel regression, and overparameterized two-layer ReLU neural networks.