Connecting Optimization and Generalization via Gradient Flow Path Length

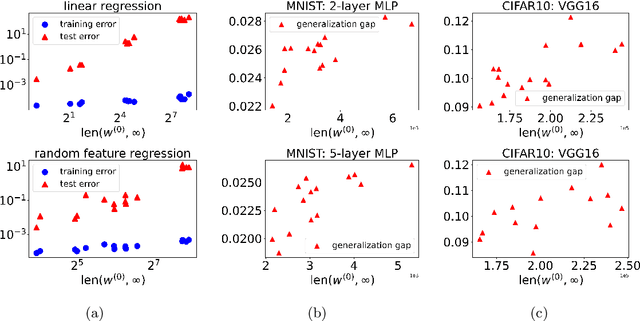
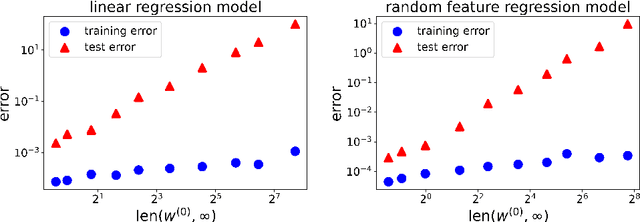
Optimization and generalization are two essential aspects of machine learning. In this paper, we propose a framework to connect optimization with generalization by analyzing the generalization error based on the length of optimization trajectory under the gradient flow algorithm after convergence. Through our approach, we show that, with a proper initialization, gradient flow converges following a short path with an explicit length estimate. Such an estimate induces a length-based generalization bound, showing that short optimization paths after convergence are associated with good generalization, which also matches our numerical results. Our framework can be applied to broad settings. For example, we use it to obtain generalization estimates on three distinct machine learning models: underdetermined $\ell_p$ linear regression, kernel regression, and overparameterized two-layer ReLU neural networks.