DynGMA: a robust approach for learning stochastic differential equations from data

Learning unknown stochastic differential equations (SDEs) from observed data is a significant and challenging task with applications in various fields. Current approaches often use neural networks to represent drift and diffusion functions, and construct likelihood-based loss by approximating the transition density to train these networks. However, these methods often rely on one-step stochastic numerical schemes, necessitating data with sufficiently high time resolution. In this paper, we introduce novel approximations to the transition density of the parameterized SDE: a Gaussian density approximation inspired by the random perturbation theory of dynamical systems, and its extension, the dynamical Gaussian mixture approximation (DynGMA). Benefiting from the robust density approximation, our method exhibits superior accuracy compared to baseline methods in learning the fully unknown drift and diffusion functions and computing the invariant distribution from trajectory data. And it is capable of handling trajectory data with low time resolution and variable, even uncontrollable, time step sizes, such as data generated from Gillespie's stochastic simulations. We then conduct several experiments across various scenarios to verify the advantages and robustness of the proposed method.

Implementation and (Inverse Modified) Error Analysis for implicitly-templated ODE-nets

We focus on learning unknown dynamics from data using ODE-nets templated on implicit numerical initial value problem solvers. First, we perform Inverse Modified error analysis of the ODE-nets using unrolled implicit schemes for ease of interpretation. It is shown that training an ODE-net using an unrolled implicit scheme returns a close approximation of an Inverse Modified Differential Equation (IMDE). In addition, we establish a theoretical basis for hyper-parameter selection when training such ODE-nets, whereas current strategies usually treat numerical integration of ODE-nets as a black box. We thus formulate an adaptive algorithm which monitors the level of error and adapts the number of (unrolled) implicit solution iterations during the training process, so that the error of the unrolled approximation is less than the current learning loss. This helps accelerate training, while maintaining accuracy. Several numerical experiments are performed to demonstrate the advantages of the proposed algorithm compared to nonadaptive unrollings, and validate the theoretical analysis. We also note that this approach naturally allows for incorporating partially known physical terms in the equations, giving rise to what is termed ``gray box" identification.

On Numerical Integration in Neural Ordinary Differential Equations

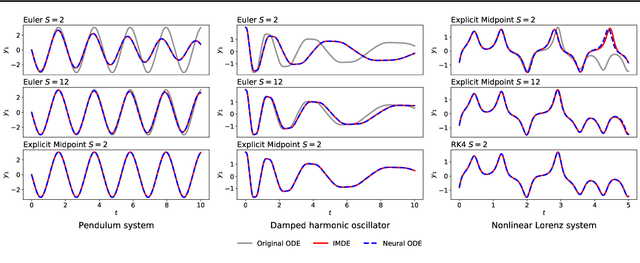
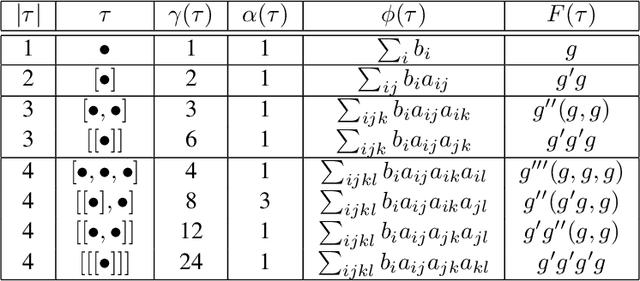
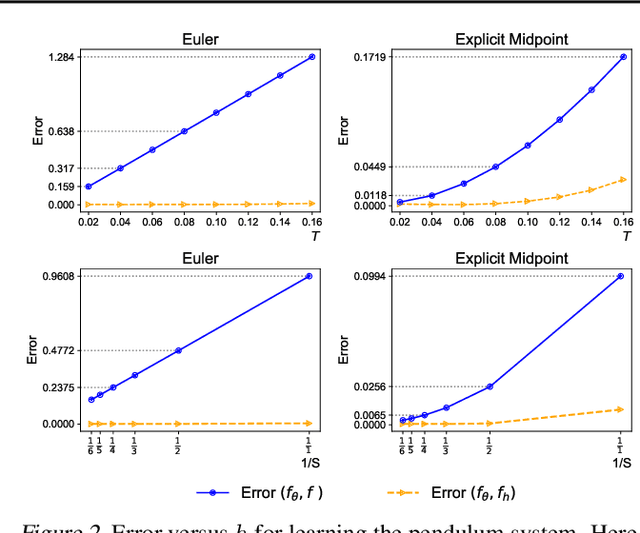
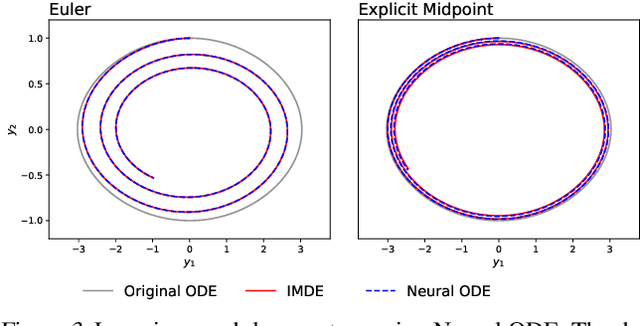
The combination of ordinary differential equations and neural networks, i.e., neural ordinary differential equations (Neural ODE), has been widely studied from various angles. However, deciphering the numerical integration in Neural ODE is still an open challenge, as many researches demonstrated that numerical integration significantly affects the performance of the model. In this paper, we propose the inverse modified differential equations (IMDE) to clarify the influence of numerical integration on training Neural ODE models. IMDE is determined by the learning task and the employed ODE solver. It is shown that training a Neural ODE model actually returns a close approximation of the IMDE, rather than the true ODE. With the help of IMDE, we deduce that (i) the discrepancy between the learned model and the true ODE is bounded by the sum of discretization error and learning loss; (ii) Neural ODE using non-symplectic numerical integration fail to learn conservation laws theoretically. Several experiments are performed to numerically verify our theoretical analysis.

VPNets: Volume-preserving neural networks for learning source-free dynamics

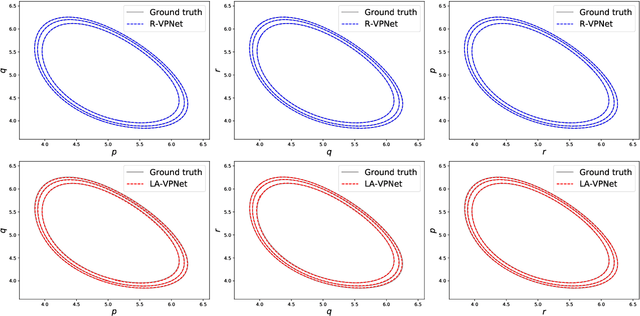
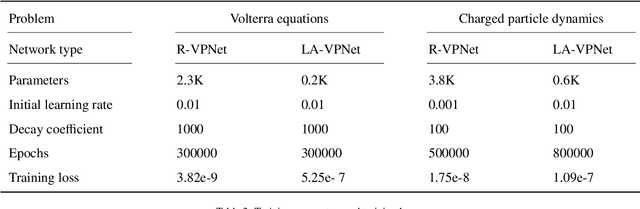
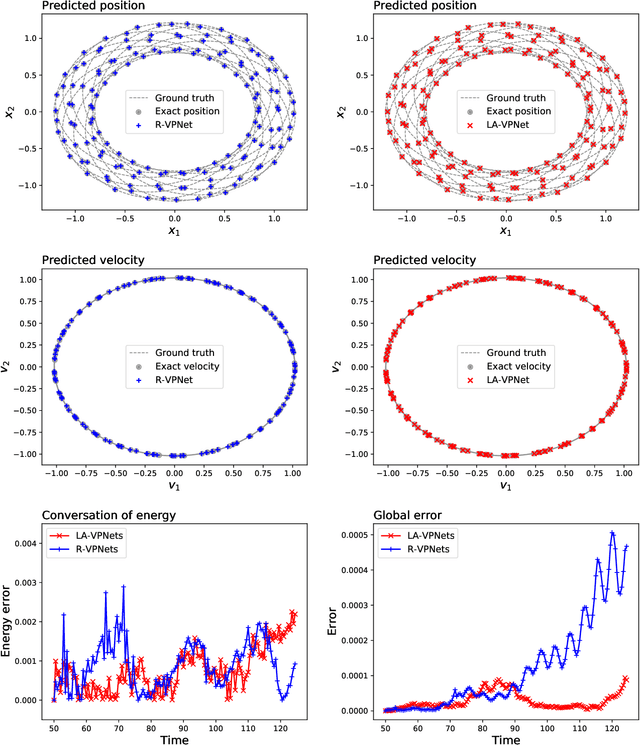
We propose volume-preserving networks (VPNets) for learning unknown source-free dynamical systems using trajectory data. We propose three modules and combine them to obtain two network architectures, coined R-VPNet and LA-VPNet. The distinct feature of the proposed models is that they are intrinsic volume-preserving. In addition, the corresponding approximation theorems are proved, which theoretically guarantee the expressivity of the proposed VPNets to learn source-free dynamics. The effectiveness, generalization ability and structure-preserving property of the VP-Nets are demonstrated by numerical experiments.

Approximation capabilities of measure-preserving neural networks

Measure-preserving neural networks are well-developed invertible models, however, the approximation capabilities remain unexplored. This paper rigorously establishes the general sufficient conditions for approximating measure-preserving maps using measure-preserving neural networks. It is shown that for compact $U \subset \R^D$ with $D\geq 2$, every measure-preserving map $\psi: U\to \R^D$ which is injective and bounded can be approximated in the $L^p$-norm by measure-preserving neural networks. Specifically, the differentiable maps with $\pm 1$ determinants of Jacobians are measure-preserving, injective and bounded on $U$, thus hold the approximation property.

Symplectic networks: Intrinsic structure-preserving networks for identifying Hamiltonian systems

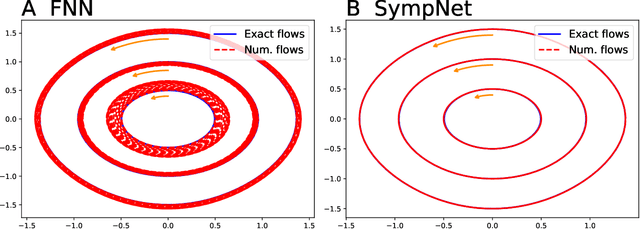
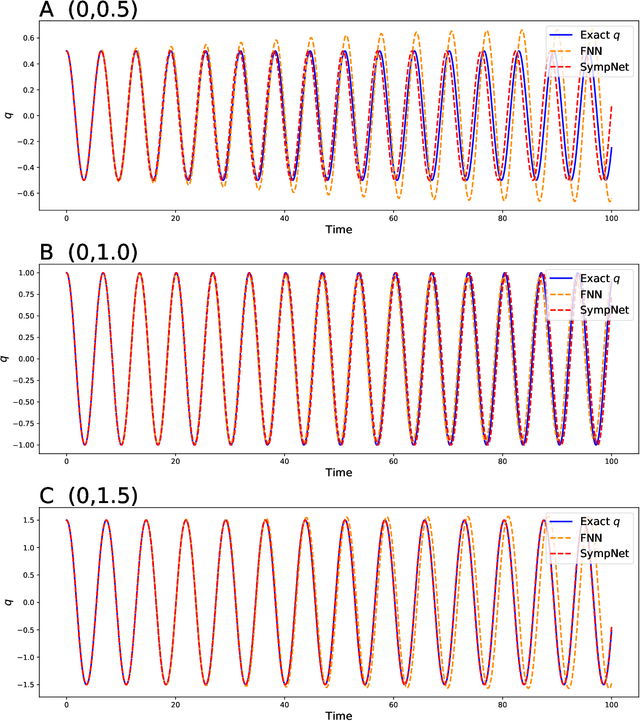
This work presents a framework of constructing the neural networks preserving the symplectic structure, so-called symplectic networks (SympNets). With the symplectic networks, we show some numerical results about (\romannumeral1) solving the Hamiltonian systems by learning abundant data points over the phase space, and (\romannumeral2) predicting the phase flows by learning a series of points depending on time. All the experiments point out that the symplectic networks perform much more better than the fully-connected networks that without any prior information, especially in the task of predicting which is unable to do within the conventional numerical methods.