Symplectic networks: Intrinsic structure-preserving networks for identifying Hamiltonian systems
Paper and Code
Jan 11, 2020
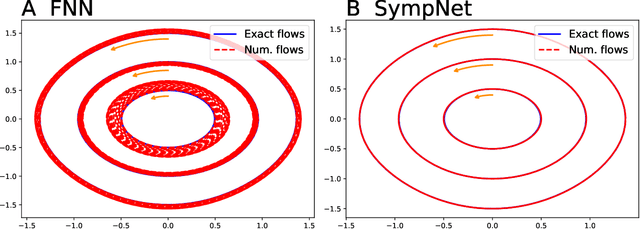

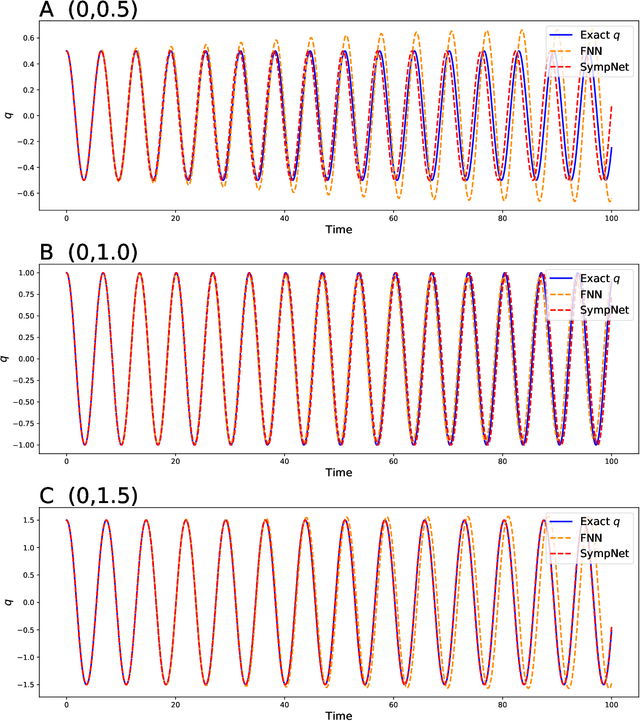
This work presents a framework of constructing the neural networks preserving the symplectic structure, so-called symplectic networks (SympNets). With the symplectic networks, we show some numerical results about (\romannumeral1) solving the Hamiltonian systems by learning abundant data points over the phase space, and (\romannumeral2) predicting the phase flows by learning a series of points depending on time. All the experiments point out that the symplectic networks perform much more better than the fully-connected networks that without any prior information, especially in the task of predicting which is unable to do within the conventional numerical methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge