A deformation-based framework for learning solution mappings of PDEs defined on varying domains

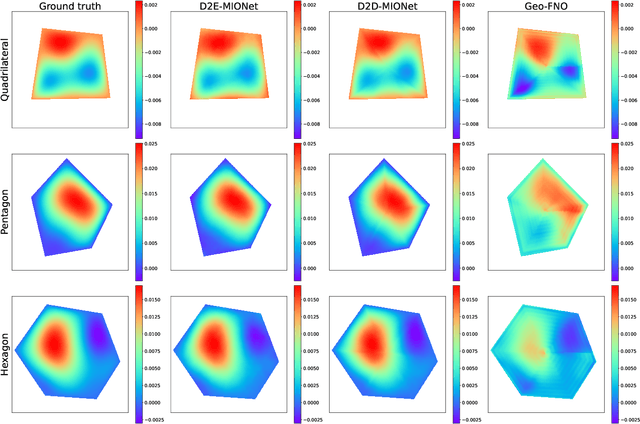
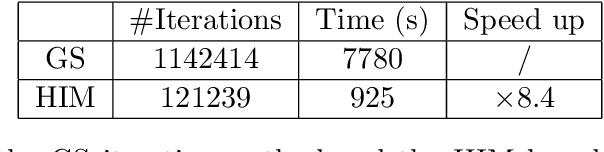
In this work, we establish a deformation-based framework for learning solution mappings of PDEs defined on varying domains. The union of functions defined on varying domains can be identified as a metric space according to the deformation, then the solution mapping is regarded as a continuous metric-to-metric mapping, and subsequently can be represented by another continuous metric-to-Banach mapping using two different strategies, referred to as the D2D framework and the D2E framework, respectively. We point out that such a metric-to-Banach mapping can be learned by neural networks, hence the solution mapping is accordingly learned. With this framework, a rigorous convergence analysis is built for the problem of learning solution mappings of PDEs on varying domains. As the theoretical framework holds based on several pivotal assumptions which need to be verified for a given specific problem, we study the star domains as a typical example, and other situations could be similarly verified. There are three important features of this framework: (1) The domains under consideration are not required to be diffeomorphic, therefore a wide range of regions can be covered by one model provided they are homeomorphic. (2) The deformation mapping is unnecessary to be continuous, thus it can be flexibly established via combining a primary identity mapping and a local deformation mapping. This capability facilitates the resolution of large systems where only local parts of the geometry undergo change. (3) If a linearity-preserving neural operator such as MIONet is adopted, this framework still preserves the linearity of the surrogate solution mapping on its source term for linear PDEs, thus it can be applied to the hybrid iterative method. We finally present several numerical experiments to validate our theoretical results.

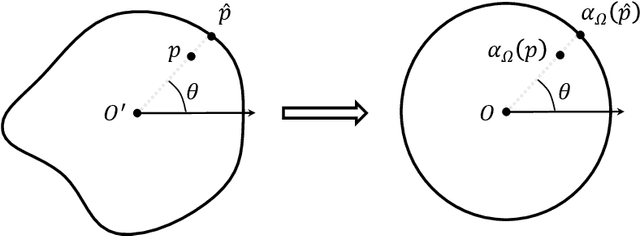
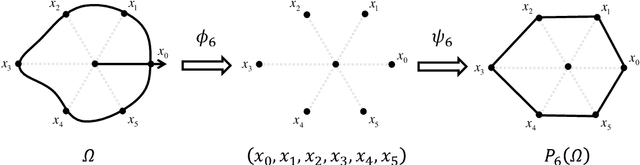
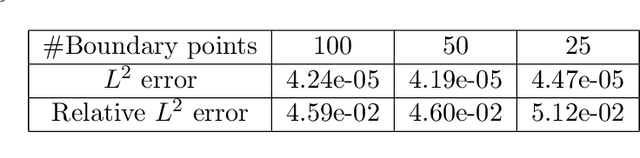
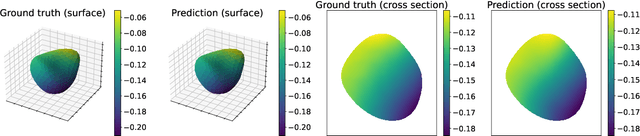
Learning solution operators of PDEs defined on varying domains via MIONet

In this work, we propose a method to learn the solution operators of PDEs defined on varying domains via MIONet, and theoretically justify this method. We first extend the approximation theory of MIONet to further deal with metric spaces, establishing that MIONet can approximate mappings with multiple inputs in metric spaces. Subsequently, we construct a set consisting of some appropriate regions and provide a metric on this set thus make it a metric space, which satisfies the approximation condition of MIONet. Building upon the theoretical foundation, we are able to learn the solution mapping of a PDE with all the parameters varying, including the parameters of the differential operator, the right-hand side term, the boundary condition, as well as the domain. Without loss of generality, we for example perform the experiments for 2-d Poisson equations, where the domains and the right-hand side terms are varying. The results provide insights into the performance of this method across convex polygons, polar regions with smooth boundary, and predictions for different levels of discretization on one task. Reasonably, we point out that this is a meshless method, hence can be flexibly used as a general solver for a type of PDE.

Generalized Lagrangian Neural Networks

Incorporating neural networks for the solution of Ordinary Differential Equations (ODEs) represents a pivotal research direction within computational mathematics. Within neural network architectures, the integration of the intrinsic structure of ODEs offers advantages such as enhanced predictive capabilities and reduced data utilization. Among these structural ODE forms, the Lagrangian representation stands out due to its significant physical underpinnings. Building upon this framework, Bhattoo introduced the concept of Lagrangian Neural Networks (LNNs). Then in this article, we introduce a groundbreaking extension (Genralized Lagrangian Neural Networks) to Lagrangian Neural Networks (LNNs), innovatively tailoring them for non-conservative systems. By leveraging the foundational importance of the Lagrangian within Lagrange's equations, we formulate the model based on the generalized Lagrange's equation. This modification not only enhances prediction accuracy but also guarantees Lagrangian representation in non-conservative systems. Furthermore, we perform various experiments, encompassing 1-dimensional and 2-dimensional examples, along with an examination of the impact of network parameters, which proved the superiority of Generalized Lagrangian Neural Networks(GLNNs).

Implementation and (Inverse Modified) Error Analysis for implicitly-templated ODE-nets

We focus on learning unknown dynamics from data using ODE-nets templated on implicit numerical initial value problem solvers. First, we perform Inverse Modified error analysis of the ODE-nets using unrolled implicit schemes for ease of interpretation. It is shown that training an ODE-net using an unrolled implicit scheme returns a close approximation of an Inverse Modified Differential Equation (IMDE). In addition, we establish a theoretical basis for hyper-parameter selection when training such ODE-nets, whereas current strategies usually treat numerical integration of ODE-nets as a black box. We thus formulate an adaptive algorithm which monitors the level of error and adapts the number of (unrolled) implicit solution iterations during the training process, so that the error of the unrolled approximation is less than the current learning loss. This helps accelerate training, while maintaining accuracy. Several numerical experiments are performed to demonstrate the advantages of the proposed algorithm compared to nonadaptive unrollings, and validate the theoretical analysis. We also note that this approach naturally allows for incorporating partially known physical terms in the equations, giving rise to what is termed ``gray box" identification.

On Numerical Integration in Neural Ordinary Differential Equations

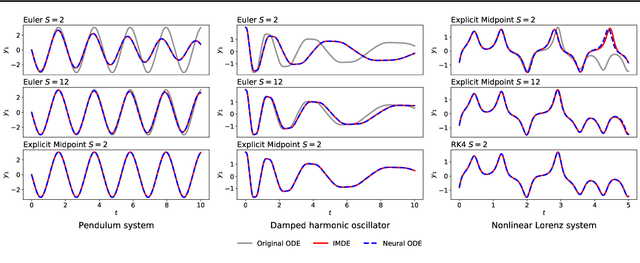
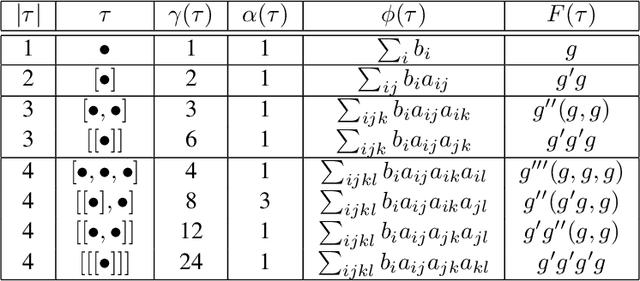
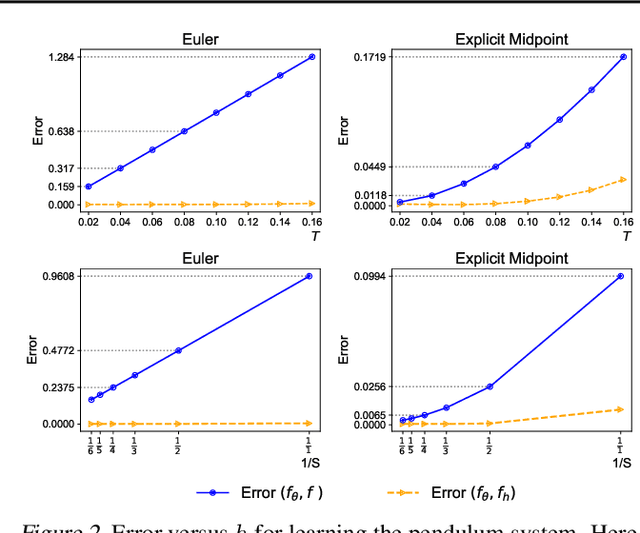
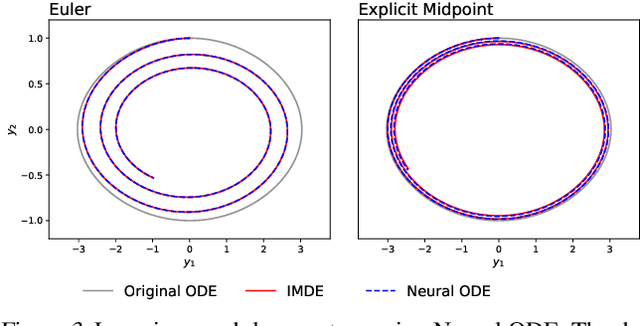
The combination of ordinary differential equations and neural networks, i.e., neural ordinary differential equations (Neural ODE), has been widely studied from various angles. However, deciphering the numerical integration in Neural ODE is still an open challenge, as many researches demonstrated that numerical integration significantly affects the performance of the model. In this paper, we propose the inverse modified differential equations (IMDE) to clarify the influence of numerical integration on training Neural ODE models. IMDE is determined by the learning task and the employed ODE solver. It is shown that training a Neural ODE model actually returns a close approximation of the IMDE, rather than the true ODE. With the help of IMDE, we deduce that (i) the discrepancy between the learned model and the true ODE is bounded by the sum of discretization error and learning loss; (ii) Neural ODE using non-symplectic numerical integration fail to learn conservation laws theoretically. Several experiments are performed to numerically verify our theoretical analysis.

VPNets: Volume-preserving neural networks for learning source-free dynamics

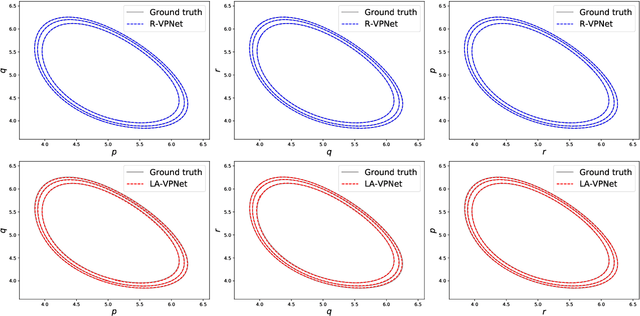
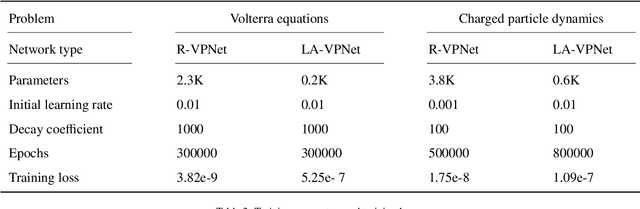
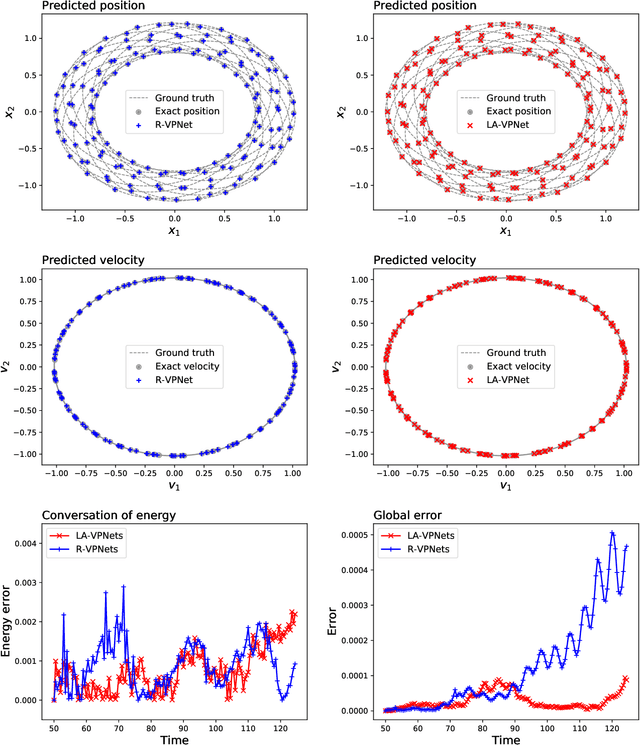
We propose volume-preserving networks (VPNets) for learning unknown source-free dynamical systems using trajectory data. We propose three modules and combine them to obtain two network architectures, coined R-VPNet and LA-VPNet. The distinct feature of the proposed models is that they are intrinsic volume-preserving. In addition, the corresponding approximation theorems are proved, which theoretically guarantee the expressivity of the proposed VPNets to learn source-free dynamics. The effectiveness, generalization ability and structure-preserving property of the VP-Nets are demonstrated by numerical experiments.

Approximation capabilities of measure-preserving neural networks

Measure-preserving neural networks are well-developed invertible models, however, the approximation capabilities remain unexplored. This paper rigorously establishes the general sufficient conditions for approximating measure-preserving maps using measure-preserving neural networks. It is shown that for compact $U \subset \R^D$ with $D\geq 2$, every measure-preserving map $\psi: U\to \R^D$ which is injective and bounded can be approximated in the $L^p$-norm by measure-preserving neural networks. Specifically, the differentiable maps with $\pm 1$ determinants of Jacobians are measure-preserving, injective and bounded on $U$, thus hold the approximation property.

Symplectic networks: Intrinsic structure-preserving networks for identifying Hamiltonian systems

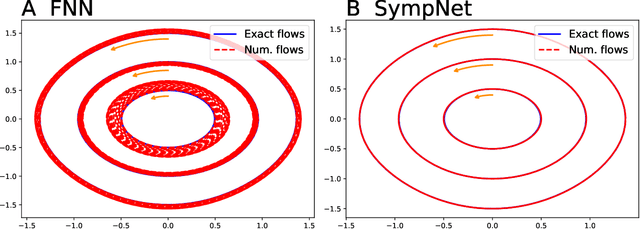
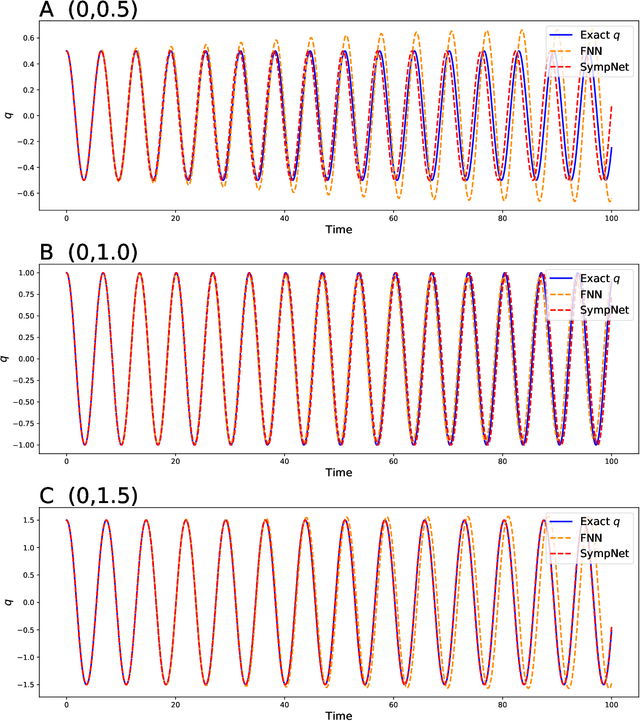
This work presents a framework of constructing the neural networks preserving the symplectic structure, so-called symplectic networks (SympNets). With the symplectic networks, we show some numerical results about (\romannumeral1) solving the Hamiltonian systems by learning abundant data points over the phase space, and (\romannumeral2) predicting the phase flows by learning a series of points depending on time. All the experiments point out that the symplectic networks perform much more better than the fully-connected networks that without any prior information, especially in the task of predicting which is unable to do within the conventional numerical methods.

Quantifying the generalization error in deep learning in terms of data distribution and neural network smoothness

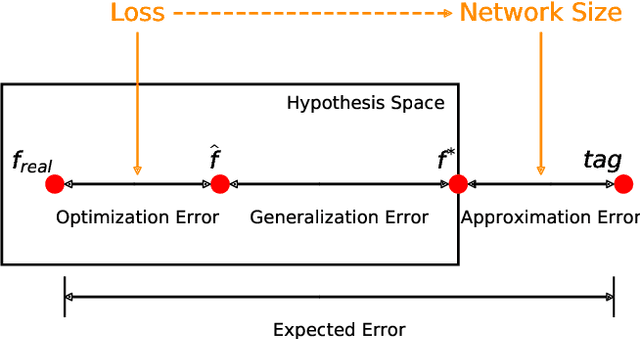
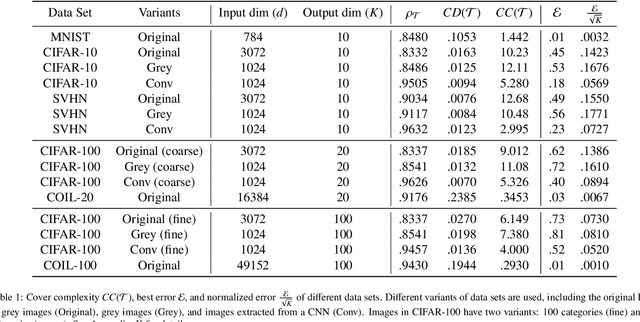
The accuracy of deep learning, i.e., deep neural networks, can be characterized by dividing the total error into three main types: approximation error, optimization error, and generalization error. Whereas there are some satisfactory answers to the problems of approximation and optimization, much less is known about the theory of generalization. Most existing theoretical works for generalization fail to explain the performance of neural networks in practice. To derive a meaningful bound, we study the generalization error of neural networks for classification problems in terms of data distribution and neural network smoothness. We introduce the cover complexity (CC) to measure the difficulty of learning a data set and the inverse of modules of continuity to quantify neural network smoothness. A quantitative bound for expected accuracy/error is derived by considering both the CC and neural network smoothness. We validate our theoretical results by several data sets of images. The numerical results verify that the expected error of trained networks scaled with the square root of the number of classes has a linear relationship with respect to the CC. In addition, we observe a clear consistency between test loss and neural network smoothness during the training process.