VPNets: Volume-preserving neural networks for learning source-free dynamics
Paper and Code
Apr 29, 2022
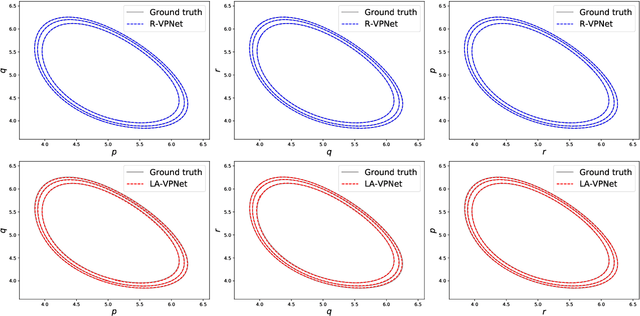
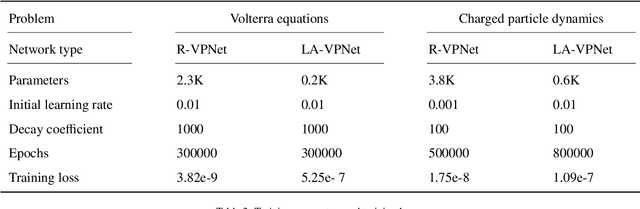
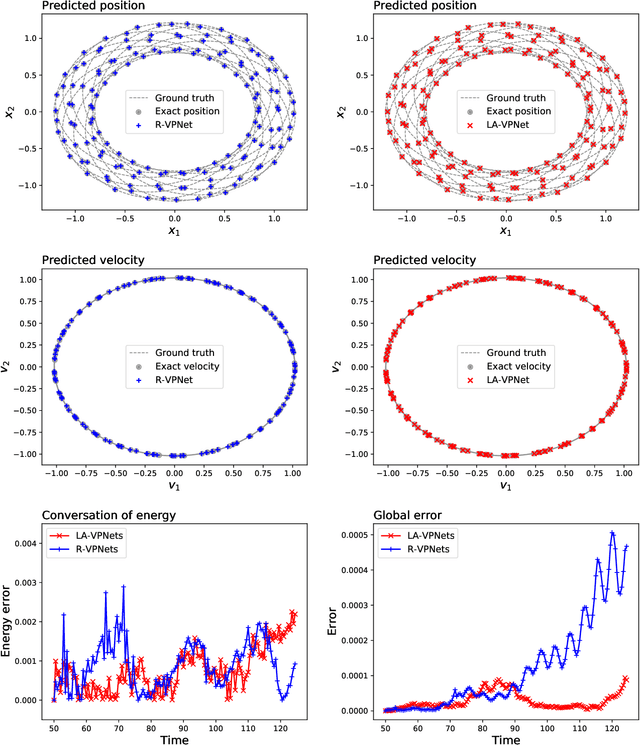
We propose volume-preserving networks (VPNets) for learning unknown source-free dynamical systems using trajectory data. We propose three modules and combine them to obtain two network architectures, coined R-VPNet and LA-VPNet. The distinct feature of the proposed models is that they are intrinsic volume-preserving. In addition, the corresponding approximation theorems are proved, which theoretically guarantee the expressivity of the proposed VPNets to learn source-free dynamics. The effectiveness, generalization ability and structure-preserving property of the VP-Nets are demonstrated by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge