LVM-GP: Uncertainty-Aware PDE Solver via coupling latent variable model and Gaussian process

We propose a novel probabilistic framework, termed LVM-GP, for uncertainty quantification in solving forward and inverse partial differential equations (PDEs) with noisy data. The core idea is to construct a stochastic mapping from the input to a high-dimensional latent representation, enabling uncertainty-aware prediction of the solution. Specifically, the architecture consists of a confidence-aware encoder and a probabilistic decoder. The encoder implements a high-dimensional latent variable model based on a Gaussian process (LVM-GP), where the latent representation is constructed by interpolating between a learnable deterministic feature and a Gaussian process prior, with the interpolation strength adaptively controlled by a confidence function learned from data. The decoder defines a conditional Gaussian distribution over the solution field, where the mean is predicted by a neural operator applied to the latent representation, allowing the model to learn flexible function-to-function mapping. Moreover, physical laws are enforced as soft constraints in the loss function to ensure consistency with the underlying PDE structure. Compared to existing approaches such as Bayesian physics-informed neural networks (B-PINNs) and deep ensembles, the proposed framework can efficiently capture functional dependencies via merging a latent Gaussian process and neural operator, resulting in competitive predictive accuracy and robust uncertainty quantification. Numerical experiments demonstrate the effectiveness and reliability of the method.

Integral regularization PINNs for evolution equations

Evolution equations, including both ordinary differential equations (ODEs) and partial differential equations (PDEs), play a pivotal role in modeling dynamic systems. However, achieving accurate long-time integration for these equations remains a significant challenge. While physics-informed neural networks (PINNs) provide a mesh-free framework for solving PDEs, they often suffer from temporal error accumulation, which limits their effectiveness in capturing long-time behaviors. To alleviate this issue, we propose integral regularization PINNs (IR-PINNs), a novel approach that enhances temporal accuracy by incorporating an integral-based residual term into the loss function. This method divides the entire time interval into smaller sub-intervals and enforces constraints over these sub-intervals, thereby improving the resolution and correlation of temporal dynamics. Furthermore, IR-PINNs leverage adaptive sampling to dynamically refine the distribution of collocation points based on the evolving solution, ensuring higher accuracy in regions with sharp gradients or rapid variations. Numerical experiments on benchmark problems demonstrate that IR-PINNs outperform original PINNs and other state-of-the-art methods in capturing long-time behaviors, offering a robust and accurate solution for evolution equations.

Estimating Committor Functions via Deep Adaptive Sampling on Rare Transition Paths

The committor functions are central to investigating rare but important events in molecular simulations. It is known that computing the committor function suffers from the curse of dimensionality. Recently, using neural networks to estimate the committor function has gained attention due to its potential for high-dimensional problems. Training neural networks to approximate the committor function needs to sample transition data from straightforward simulations of rare events, which is very inefficient. The scarcity of transition data makes it challenging to approximate the committor function. To address this problem, we propose an efficient framework to generate data points in the transition state region that helps train neural networks to approximate the committor function. We design a Deep Adaptive Sampling method for TRansition paths (DASTR), where deep generative models are employed to generate samples to capture the information of transitions effectively. In particular, we treat a non-negative function in the integrand of the loss functional as an unnormalized probability density function and approximate it with the deep generative model. The new samples from the deep generative model are located in the transition state region and fewer samples are located in the other region. This distribution provides effective samples for approximating the committor function and significantly improves the accuracy. We demonstrate the effectiveness of the proposed method through both simulations and realistic examples.

A hybrid FEM-PINN method for time-dependent partial differential equations

In this work, we present a hybrid numerical method for solving evolution partial differential equations (PDEs) by merging the time finite element method with deep neural networks. In contrast to the conventional deep learning-based formulation where the neural network is defined on a spatiotemporal domain, our methodology utilizes finite element basis functions in the time direction where the space-dependent coefficients are defined as the output of a neural network. We then apply the Galerkin or collocation projection in the time direction to obtain a system of PDEs for the space-dependent coefficients which is approximated in the framework of PINN. The advantages of such a hybrid formulation are twofold: statistical errors are avoided for the integral in the time direction, and the neural network's output can be regarded as a set of reduced spatial basis functions. To further alleviate the difficulties from high dimensionality and low regularity, we have developed an adaptive sampling strategy that refines the training set. More specifically, we use an explicit density model to approximate the distribution induced by the PDE residual and then augment the training set with new time-dependent random samples given by the learned density model. The effectiveness and efficiency of our proposed method have been demonstrated through a series of numerical experiments.

Deep adaptive sampling for surrogate modeling without labeled data

Surrogate modeling is of great practical significance for parametric differential equation systems. In contrast to classical numerical methods, using physics-informed deep learning methods to construct simulators for such systems is a promising direction due to its potential to handle high dimensionality, which requires minimizing a loss over a training set of random samples. However, the random samples introduce statistical errors, which may become the dominant errors for the approximation of low-regularity and high-dimensional problems. In this work, we present a deep adaptive sampling method for surrogate modeling ($\text{DAS}^2$), where we generalize the deep adaptive sampling (DAS) method [62] [Tang, Wan and Yang, 2023] to build surrogate models for low-regularity parametric differential equations. In the parametric setting, the residual loss function can be regarded as an unnormalized probability density function (PDF) of the spatial and parametric variables. This PDF is approximated by a deep generative model, from which new samples are generated and added to the training set. Since the new samples match the residual-induced distribution, the refined training set can further reduce the statistical error in the current approximate solution. We demonstrate the effectiveness of $\text{DAS}^2$ with a series of numerical experiments, including the parametric lid-driven 2D cavity flow problem with a continuous range of Reynolds numbers from 100 to 1000.

Adaptive importance sampling for Deep Ritz

We introduce an adaptive sampling method for the Deep Ritz method aimed at solving partial differential equations (PDEs). Two deep neural networks are used. One network is employed to approximate the solution of PDEs, while the other one is a deep generative model used to generate new collocation points to refine the training set. The adaptive sampling procedure consists of two main steps. The first step is solving the PDEs using the Deep Ritz method by minimizing an associated variational loss discretized by the collocation points in the training set. The second step involves generating a new training set, which is then used in subsequent computations to further improve the accuracy of the current approximate solution. We treat the integrand in the variational loss as an unnormalized probability density function (PDF) and approximate it using a deep generative model called bounded KRnet. The new samples and their associated PDF values are obtained from the bounded KRnet. With these new samples and their associated PDF values, the variational loss can be approximated more accurately by importance sampling. Compared to the original Deep Ritz method, the proposed adaptive method improves accuracy, especially for problems characterized by low regularity and high dimensionality. We demonstrate the effectiveness of our new method through a series of numerical experiments.

Adversarial Adaptive Sampling: Unify PINN and Optimal Transport for the Approximation of PDEs

Solving partial differential equations (PDEs) is a central task in scientific computing. Recently, neural network approximation of PDEs has received increasing attention due to its flexible meshless discretization and its potential for high-dimensional problems. One fundamental numerical difficulty is that random samples in the training set introduce statistical errors into the discretization of loss functional which may become the dominant error in the final approximation, and therefore overshadow the modeling capability of the neural network. In this work, we propose a new minmax formulation to optimize simultaneously the approximate solution, given by a neural network model, and the random samples in the training set, provided by a deep generative model. The key idea is to use a deep generative model to adjust random samples in the training set such that the residual induced by the approximate PDE solution can maintain a smooth profile when it is being minimized. Such an idea is achieved by implicitly embedding the Wasserstein distance between the residual-induced distribution and the uniform distribution into the loss, which is then minimized together with the residual. A nearly uniform residual profile means that its variance is small for any normalized weight function such that the Monte Carlo approximation error of the loss functional is reduced significantly for a certain sample size. The adversarial adaptive sampling (AAS) approach proposed in this work is the first attempt to formulate two essential components, minimizing the residual and seeking the optimal training set, into one minmax objective functional for the neural network approximation of PDEs.

Bounded KRnet and its applications to density estimation and approximation

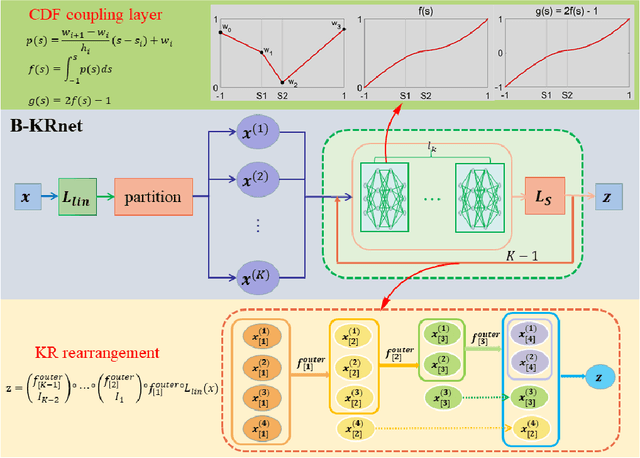
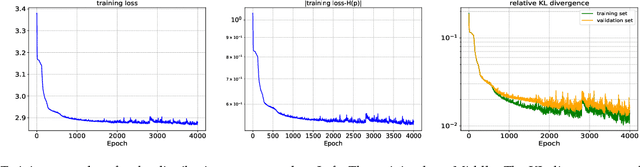
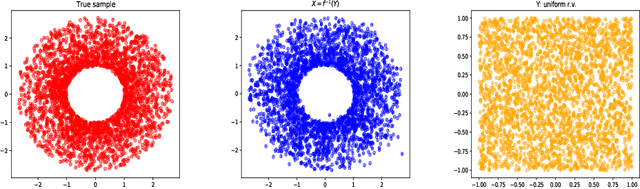
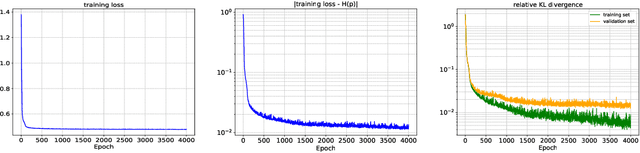
In this paper, we develop an invertible mapping, called B-KRnet, on a bounded domain and apply it to density estimation/approximation for data or the solutions of PDEs such as the Fokker-Planck equation and the Keller-Segel equation. Similar to KRnet, the structure of B-KRnet adapts the triangular form of the Knothe-Rosenblatt rearrangement into a normalizing flow model. The main difference between B-KRnet and KRnet is that B-KRnet is defined on a hypercube while KRnet is defined on the whole space, in other words, we introduce a new mechanism in B-KRnet to maintain the exact invertibility. Using B-KRnet as a transport map, we obtain an explicit probability density function (PDF) model that corresponds to the pushforward of a prior (uniform) distribution on the hypercube. To approximate PDFs defined on a bounded computational domain, B-KRnet is more effective than KRnet. By coupling KRnet and B-KRnet, we can also define a deep generative model on a high-dimensional domain where some dimensions are bounded and other dimensions are unbounded. A typical case is the solution of the stationary kinetic Fokker-Planck equation, which is a PDF of position and momentum. Based on B-KRnet, we develop an adaptive learning approach to approximate partial differential equations whose solutions are PDFs or can be regarded as a PDF. In addition, we apply B-KRnet to density estimation when only data are available. A variety of numerical experiments is presented to demonstrate the effectiveness of B-KRnet.

Dimension-reduced KRnet maps for high-dimensional Bayesian inverse problems

We present a dimension-reduced KRnet map approach (DR-KRnet) for high-dimensional Bayesian inverse problems, which is based on an explicit construction of a map that pushes forward the prior measure to the posterior measure in the latent space. Our approach consists of two main components: data-driven VAE prior and density approximation of the posterior of the latent variable. In reality, it may not be trivial to initialize a prior distribution that is consistent with available prior data; in other words, the complex prior information is often beyond simple hand-crafted priors. We employ variational autoencoder (VAE) to approximate the underlying distribution of the prior dataset, which is achieved through a latent variable and a decoder. Using the decoder provided by the VAE prior, we reformulate the problem in a low-dimensional latent space. In particular, we seek an invertible transport map given by KRnet to approximate the posterior distribution of the latent variable. Moreover, an efficient physics-constrained surrogate model without any labeled data is constructed to reduce the computational cost of solving both forward and adjoint problems involved in likelihood computation. With numerical experiments, we demonstrate the accuracy and efficiency of DR-KRnet for high-dimensional Bayesian inverse problems.

Adaptive deep density approximation for fractional Fokker-Planck equations

In this work, we propose adaptive deep learning approaches based on normalizing flows for solving fractional Fokker-Planck equations (FPEs). The solution of a FPE is a probability density function (PDF). Traditional mesh-based methods are ineffective because of the unbounded computation domain, a large number of dimensions and the nonlocal fractional operator. To this end, we represent the solution with an explicit PDF model induced by a flow-based deep generative model, simplified KRnet, which constructs a transport map from a simple distribution to the target distribution. We consider two methods to approximate the fractional Laplacian. One method is the Monte Carlo approximation. The other method is to construct an auxiliary model with Gaussian radial basis functions (GRBFs) to approximate the solution such that we may take advantage of the fact that the fractional Laplacian of a Gaussian is known analytically. Based on these two different ways for the approximation of the fractional Laplacian, we propose two models, MCNF and GRBFNF, to approximate stationary FPEs and MCTNF to approximate time-dependent FPEs. To further improve the accuracy, we refine the training set and the approximate solution alternately. A variety of numerical examples is presented to demonstrate the effectiveness of our adaptive deep density approaches.