DocMEdit: Towards Document-Level Model Editing

Model editing aims to correct errors and outdated knowledge in the Large language models (LLMs) with minimal cost. Prior research has proposed a variety of datasets to assess the effectiveness of these model editing methods. However, most existing datasets only require models to output short phrases or sentences, overlooks the widespread existence of document-level tasks in the real world, raising doubts about their practical usability. Aimed at addressing this limitation and promoting the application of model editing in real-world scenarios, we propose the task of document-level model editing. To tackle such challenges and enhance model capabilities in practical settings, we introduce \benchmarkname, a dataset focused on document-level model editing, characterized by document-level inputs and outputs, extrapolative, and multiple facts within a single edit. We propose a series of evaluation metrics and experiments. The results show that the difficulties in document-level model editing pose challenges for existing model editing methods.

EDBench: Large-Scale Electron Density Data for Molecular Modeling

Existing molecular machine learning force fields (MLFFs) generally focus on the learning of atoms, molecules, and simple quantum chemical properties (such as energy and force), but ignore the importance of electron density (ED) $\rho(r)$ in accurately understanding molecular force fields (MFFs). ED describes the probability of finding electrons at specific locations around atoms or molecules, which uniquely determines all ground state properties (such as energy, molecular structure, etc.) of interactive multi-particle systems according to the Hohenberg-Kohn theorem. However, the calculation of ED relies on the time-consuming first-principles density functional theory (DFT) which leads to the lack of large-scale ED data and limits its application in MLFFs. In this paper, we introduce EDBench, a large-scale, high-quality dataset of ED designed to advance learning-based research at the electronic scale. Built upon the PCQM4Mv2, EDBench provides accurate ED data, covering 3.3 million molecules. To comprehensively evaluate the ability of models to understand and utilize electronic information, we design a suite of ED-centric benchmark tasks spanning prediction, retrieval, and generation. Our evaluation on several state-of-the-art methods demonstrates that learning from EDBench is not only feasible but also achieves high accuracy. Moreover, we show that learning-based method can efficiently calculate ED with comparable precision while significantly reducing the computational cost relative to traditional DFT calculations. All data and benchmarks from EDBench will be freely available, laying a robust foundation for ED-driven drug discovery and materials science.

High-Throughput LLM inference on Heterogeneous Clusters

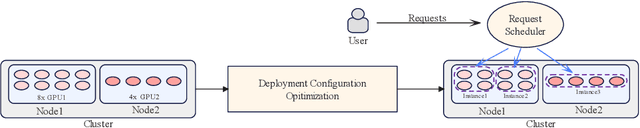
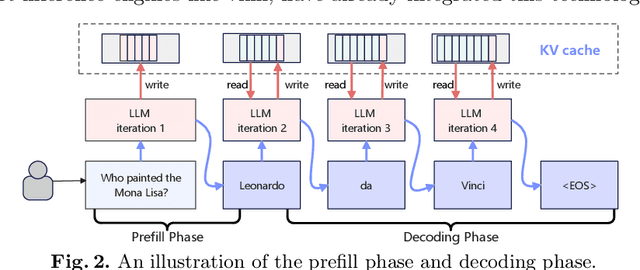
Nowadays, many companies possess various types of AI accelerators, forming heterogeneous clusters. Efficiently leveraging these clusters for high-throughput large language model (LLM) inference services can significantly reduce costs and expedite task processing. However, LLM inference on heterogeneous clusters presents two main challenges. Firstly, different deployment configurations can result in vastly different performance. The number of possible configurations is large, and evaluating the effectiveness of a specific setup is complex. Thus, finding an optimal configuration is not an easy task. Secondly, LLM inference instances within a heterogeneous cluster possess varying processing capacities, leading to different processing speeds for handling inference requests. Evaluating these capacities and designing a request scheduling algorithm that fully maximizes the potential of each instance is challenging. In this paper, we propose a high-throughput inference service system on heterogeneous clusters. First, the deployment configuration is optimized by modeling the resource amount and expected throughput and using the exhaustive search method. Second, a novel mechanism is proposed to schedule requests among instances, which fully considers the different processing capabilities of various instances. Extensive experiments show that the proposed scheduler improves throughput by 122.5% and 33.6% on two heterogeneous clusters, respectively.

FAME: Towards Factual Multi-Task Model Editing

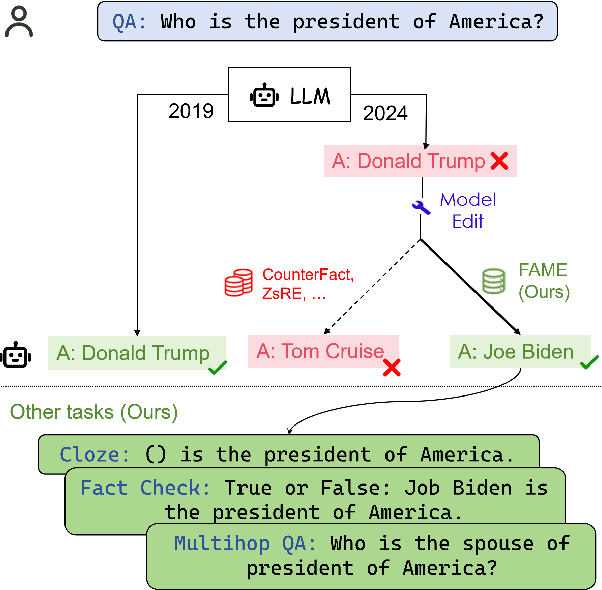
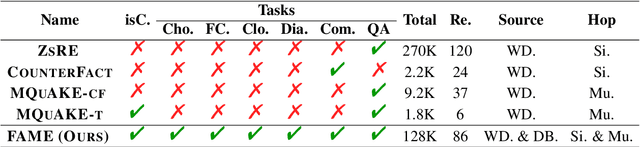
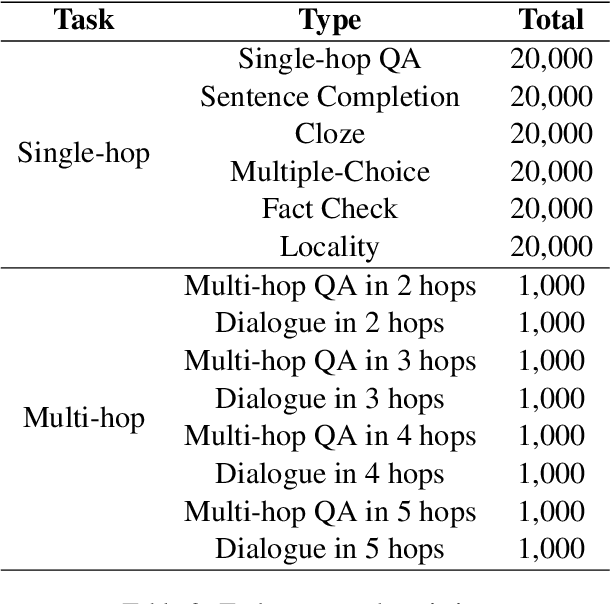
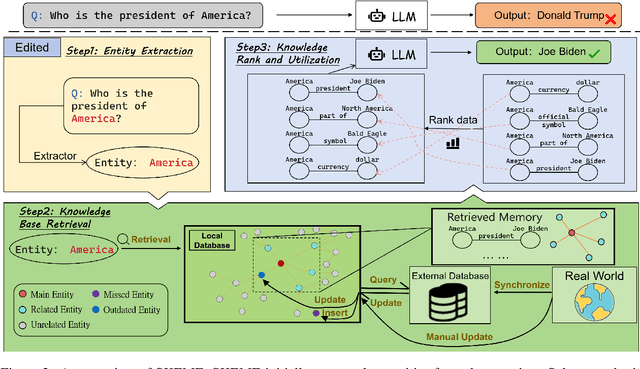
Large language models (LLMs) embed extensive knowledge and utilize it to perform exceptionally well across various tasks. Nevertheless, outdated knowledge or factual errors within LLMs can lead to misleading or incorrect responses, causing significant issues in practical applications. To rectify the fatal flaw without the necessity for costly model retraining, various model editing approaches have been proposed to correct inaccurate knowledge within LLMs in a cost-efficient way. To evaluate these model editing methods, previous work introduced a series of datasets. However, most of the previous datasets only contain fabricated data in a single format, which diverges from real-world model editing scenarios, raising doubts about their usability in practice. To facilitate the application of model editing in real-world scenarios, we propose the challenge of practicality. To resolve such challenges and effectively enhance the capabilities of LLMs, we present FAME, an factual, comprehensive, and multi-task dataset, which is designed to enhance the practicality of model editing. We then propose SKEME, a model editing method that uses a novel caching mechanism to ensure synchronization with the real world. The experiments demonstrate that SKEME performs excellently across various tasks and scenarios, confirming its practicality.

LocMoE+: Enhanced Router with Token Feature Awareness for Efficient LLM Pre-Training

Mixture-of-Experts (MoE) architectures have recently gained increasing popularity within the domain of large language models (LLMs) due to their ability to significantly reduce training and inference overhead. However, MoE architectures face challenges, such as significant disparities in the number of tokens assigned to each expert and a tendency toward homogenization among experts, which adversely affects the model's semantic generation capabilities. In this paper, we introduce LocMoE+, a refined version of the low-overhead LocMoE, incorporating the following enhancements: (1) Quantification and definition of the affinity between experts and tokens. (2) Implementation of a global-level adaptive routing strategy to rearrange tokens based on their affinity scores. (3) Reestimation of the lower bound for expert capacity, which has been shown to progressively decrease as the token feature distribution evolves. Experimental results demonstrate that, without compromising model convergence or efficacy, the number of tokens each expert processes can be reduced by over 60%. Combined with communication optimizations, this leads to an average improvement in training efficiency ranging from 5.4% to 46.6%. After fine-tuning, LocMoE+ exhibits a performance improvement of 9.7% to 14.1% across the GDAD, C-Eval, and TeleQnA datasets.

EFSA: Towards Event-Level Financial Sentiment Analysis

In this paper, we extend financial sentiment analysis~(FSA) to event-level since events usually serve as the subject of the sentiment in financial text. Though extracting events from the financial text may be conducive to accurate sentiment predictions, it has specialized challenges due to the lengthy and discontinuity of events in a financial text. To this end, we reconceptualize the event extraction as a classification task by designing a categorization comprising coarse-grained and fine-grained event categories. Under this setting, we formulate the \textbf{E}vent-Level \textbf{F}inancial \textbf{S}entiment \textbf{A}nalysis~(\textbf{EFSA} for short) task that outputs quintuples consisting of (company, industry, coarse-grained event, fine-grained event, sentiment) from financial text. A large-scale Chinese dataset containing $12,160$ news articles and $13,725$ quintuples is publicized as a brand new testbed for our task. A four-hop Chain-of-Thought LLM-based approach is devised for this task. Systematically investigations are conducted on our dataset, and the empirical results demonstrate the benchmarking scores of existing methods and our proposed method can reach the current state-of-the-art. Our dataset and framework implementation are available at https://anonymous.4open.science/r/EFSA-645E

Transform then Explore: a Simple and Effective Technique for Exploratory Combinatorial Optimization with Reinforcement Learning

Many complex problems encountered in both production and daily life can be conceptualized as combinatorial optimization problems (COPs) over graphs. Recent years, reinforcement learning (RL) based models have emerged as a promising direction, which treat the COPs solving as a heuristic learning problem. However, current finite-horizon-MDP based RL models have inherent limitations. They are not allowed to explore adquately for improving solutions at test time, which may be necessary given the complexity of NP-hard optimization tasks. Some recent attempts solve this issue by focusing on reward design and state feature engineering, which are tedious and ad-hoc. In this work, we instead propose a much simpler but more effective technique, named gauge transformation (GT). The technique is originated from physics, but is very effective in enabling RL agents to explore to continuously improve the solutions during test. Morever, GT is very simple, which can be implemented with less than 10 lines of Python codes, and can be applied to a vast majority of RL models. Experimentally, we show that traditional RL models with GT technique produce the state-of-the-art performances on the MaxCut problem. Furthermore, since GT is independent of any RL models, it can be seamlessly integrated into various RL frameworks, paving the way of these models for more effective explorations in the solving of general COPs.

Satellite Federated Edge Learning: Architecture Design and Convergence Analysis

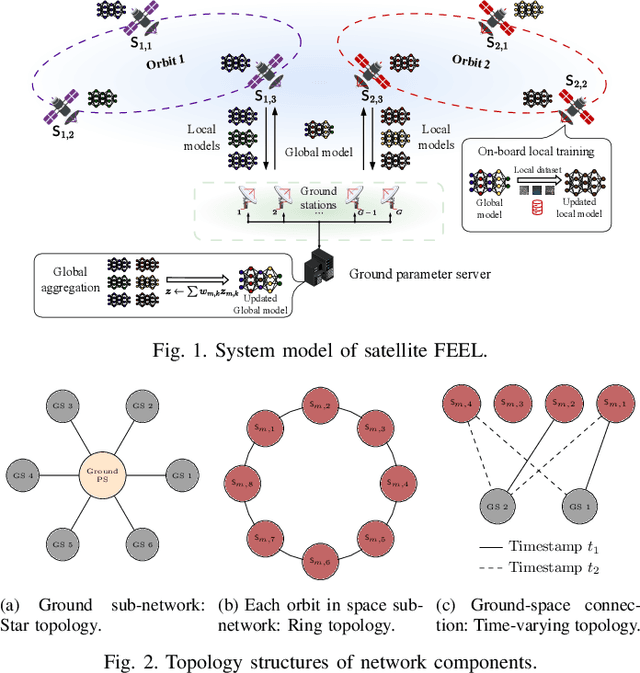
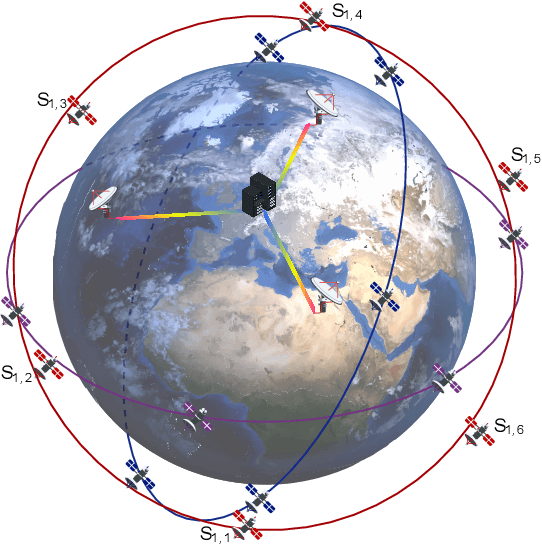
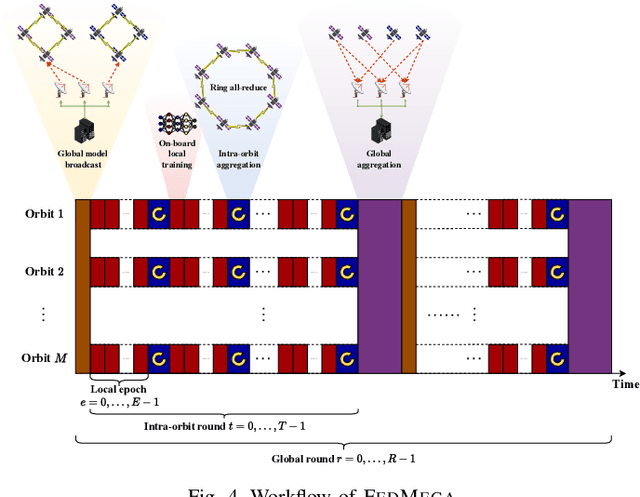
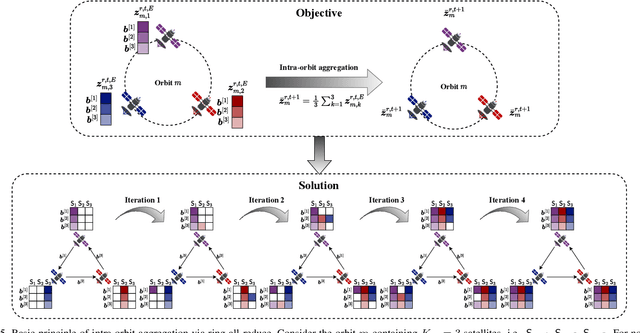
The proliferation of low-earth-orbit (LEO) satellite networks leads to the generation of vast volumes of remote sensing data which is traditionally transferred to the ground server for centralized processing, raising privacy and bandwidth concerns. Federated edge learning (FEEL), as a distributed machine learning approach, has the potential to address these challenges by sharing only model parameters instead of raw data. Although promising, the dynamics of LEO networks, characterized by the high mobility of satellites and short ground-to-satellite link (GSL) duration, pose unique challenges for FEEL. Notably, frequent model transmission between the satellites and ground incurs prolonged waiting time and large transmission latency. This paper introduces a novel FEEL algorithm, named FEDMEGA, tailored to LEO mega-constellation networks. By integrating inter-satellite links (ISL) for intra-orbit model aggregation, the proposed algorithm significantly reduces the usage of low data rate and intermittent GSL. Our proposed method includes a ring all-reduce based intra-orbit aggregation mechanism, coupled with a network flow-based transmission scheme for global model aggregation, which enhances transmission efficiency. Theoretical convergence analysis is provided to characterize the algorithm performance. Extensive simulations show that our FEDMEGA algorithm outperforms existing satellite FEEL algorithms, exhibiting an approximate 30% improvement in convergence rate.

LocMoE: A Low-overhead MoE for Large Language Model Training

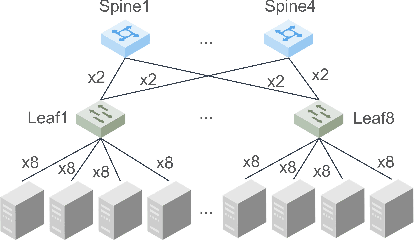
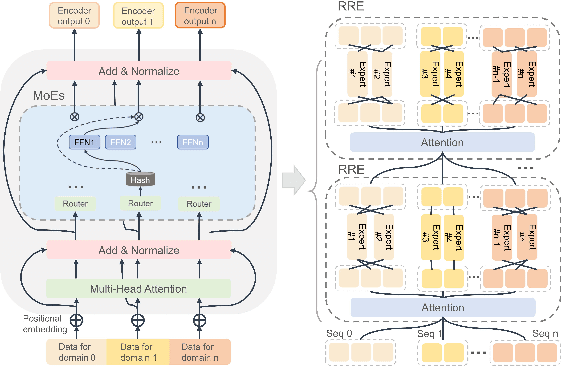
The Mixtures-of-Experts (MoE) model is a widespread distributed and integrated learning method for large language models (LLM), which is favored due to its ability to sparsify and expand models efficiently. However, the performance of MoE is limited by load imbalance and high latency of All-To-All communication, along with relatively redundant computation owing to large expert capacity. Load imbalance may result from existing routing policies that consistently tend to select certain experts. The frequent inter-node communication in the All-To-All procedure also significantly prolongs the training time. To alleviate the above performance problems, we propose a novel routing strategy that combines load balance and locality by converting partial inter-node communication to that of intra-node. Notably, we elucidate that there is a minimum threshold for expert capacity, calculated through the maximal angular deviation between the gating weights of the experts and the assigned tokens. We port these modifications on the PanGu-Sigma model based on the MindSpore framework with multi-level routing and conduct experiments on Ascend clusters. The experiment results demonstrate that the proposed LocMoE reduces training time per epoch by 12.68% to 22.24% compared to classical routers, such as hash router and switch router, without impacting the model accuracy.

Comprehensive evaluation of deep and graph learning on drug-drug interactions prediction

Recent advances and achievements of artificial intelligence (AI) as well as deep and graph learning models have established their usefulness in biomedical applications, especially in drug-drug interactions (DDIs). DDIs refer to a change in the effect of one drug to the presence of another drug in the human body, which plays an essential role in drug discovery and clinical research. DDIs prediction through traditional clinical trials and experiments is an expensive and time-consuming process. To correctly apply the advanced AI and deep learning, the developer and user meet various challenges such as the availability and encoding of data resources, and the design of computational methods. This review summarizes chemical structure based, network based, NLP based and hybrid methods, providing an updated and accessible guide to the broad researchers and development community with different domain knowledge. We introduce widely-used molecular representation and describe the theoretical frameworks of graph neural network models for representing molecular structures. We present the advantages and disadvantages of deep and graph learning methods by performing comparative experiments. We discuss the potential technical challenges and highlight future directions of deep and graph learning models for accelerating DDIs prediction.