LocMoE+: Enhanced Router with Token Feature Awareness for Efficient LLM Pre-Training

Mixture-of-Experts (MoE) architectures have recently gained increasing popularity within the domain of large language models (LLMs) due to their ability to significantly reduce training and inference overhead. However, MoE architectures face challenges, such as significant disparities in the number of tokens assigned to each expert and a tendency toward homogenization among experts, which adversely affects the model's semantic generation capabilities. In this paper, we introduce LocMoE+, a refined version of the low-overhead LocMoE, incorporating the following enhancements: (1) Quantification and definition of the affinity between experts and tokens. (2) Implementation of a global-level adaptive routing strategy to rearrange tokens based on their affinity scores. (3) Reestimation of the lower bound for expert capacity, which has been shown to progressively decrease as the token feature distribution evolves. Experimental results demonstrate that, without compromising model convergence or efficacy, the number of tokens each expert processes can be reduced by over 60%. Combined with communication optimizations, this leads to an average improvement in training efficiency ranging from 5.4% to 46.6%. After fine-tuning, LocMoE+ exhibits a performance improvement of 9.7% to 14.1% across the GDAD, C-Eval, and TeleQnA datasets.

Stochastic Distributed Optimization under Average Second-order Similarity: Algorithms and Analysis

We study finite-sum distributed optimization problems with $n$-clients under popular $\delta$-similarity condition and $\mu$-strong convexity. We propose two new algorithms: SVRS and AccSVRS motivated by previous works. The non-accelerated SVRS method combines the techniques of gradient-sliding and variance reduction, which achieves superior communication complexity $\tilde{\gO}(n {+} \sqrt{n}\delta/\mu)$ compared to existing non-accelerated algorithms. Applying the framework proposed in Katyusha X, we also build a direct accelerated practical version named AccSVRS with totally smoothness-free $\tilde{\gO}(n {+} n^{3/4}\sqrt{\delta/\mu})$ communication complexity that improves upon existing algorithms on ill-conditioning cases. Furthermore, we show a nearly matched lower bound to verify the tightness of our AccSVRS method.

On the Convergence of Policy in Unregularized Policy Mirror Descent

In this short note, we give the convergence analysis of the policy in the recent famous policy mirror descent (PMD). We mainly consider the unregularized setting following [11] with generalized Bregman divergence. The difference is that we directly give the convergence rates of policy under generalized Bregman divergence. Our results are inspired by the convergence of value function in previous works and are an extension study of policy mirror descent. Though some results have already appeared in previous work, we further discover a large body of Bregman divergences could give finite-step convergence to an optimal policy, such as the classical Euclidean distance.

Global Convergence Analysis of Deep Linear Networks with A One-neuron Layer

In this paper, we follow Eftekhari's work to give a non-local convergence analysis of deep linear networks. Specifically, we consider optimizing deep linear networks which have a layer with one neuron under quadratic loss. We describe the convergent point of trajectories with arbitrary starting point under gradient flow, including the paths which converge to one of the saddle points or the original point. We also show specific convergence rates of trajectories that converge to the global minimizer by stages. To achieve these results, this paper mainly extends the machinery in Eftekhari's work to provably identify the rank-stable set and the global minimizer convergent set. We also give specific examples to show the necessity of our definitions. Crucially, as far as we know, our results appear to be the first to give a non-local global analysis of linear neural networks from arbitrary initialized points, rather than the lazy training regime which has dominated the literature of neural networks, and restricted benign initialization in Eftekhari's work. We also note that extending our results to general linear networks without one hidden neuron assumption remains a challenging open problem.

Directional Convergence Analysis under Spherically Symmetric Distribution

We consider the fundamental problem of learning linear predictors (i.e., separable datasets with zero margin) using neural networks with gradient flow or gradient descent. Under the assumption of spherically symmetric data distribution, we show directional convergence guarantees with exact convergence rate for two-layer non-linear networks with only two hidden nodes, and (deep) linear networks. Moreover, our discovery is built on dynamic from the initialization without both initial loss and perfect classification constraint in contrast to previous works. We also point out and study the challenges in further strengthening and generalizing our results.

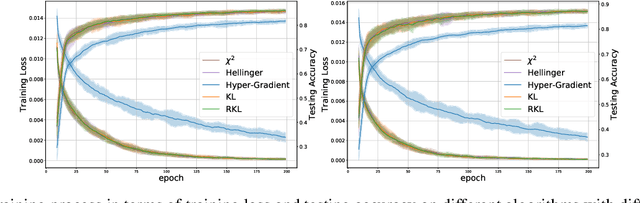
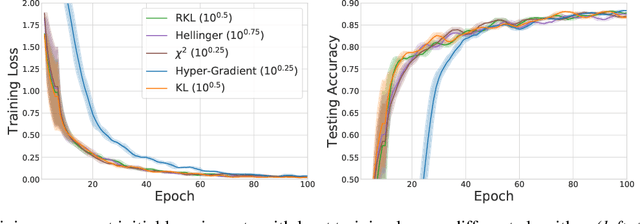
Meta-Regularization: An Approach to Adaptive Choice of the Learning Rate in Gradient Descent

We propose \textit{Meta-Regularization}, a novel approach for the adaptive choice of the learning rate in first-order gradient descent methods. Our approach modifies the objective function by adding a regularization term on the learning rate, and casts the joint updating process of parameters and learning rates into a maxmin problem. Given any regularization term, our approach facilitates the generation of practical algorithms. When \textit{Meta-Regularization} takes the $\varphi$-divergence as a regularizer, the resulting algorithms exhibit comparable theoretical convergence performance with other first-order gradient-based algorithms. Furthermore, we theoretically prove that some well-designed regularizers can improve the convergence performance under the strong-convexity condition of the objective function. Numerical experiments on benchmark problems demonstrate the effectiveness of algorithms derived from some common $\varphi$-divergence in full batch as well as online learning settings.

Landscape of Sparse Linear Network: A Brief Investigation

Network pruning, or sparse network has a long history and practical significance in modern application. A major concern for neural network training is that the non-convexity of the associated loss functions may cause bad landscape. We focus on analyzing sparse linear network generated from weight pruning strategy. With no unrealistic assumption, we prove the following statements for the squared loss objective of sparse linear neural networks: 1) every local minimum is a global minimum for scalar output with any sparse structure, or non-intersect sparse first layer and dense other layers with whitened data; 2) sparse linear networks have sub-optimal local-min for only sparse first layer or three target dimensions.

Optimal Quantization for Batch Normalization in Neural Network Deployments and Beyond

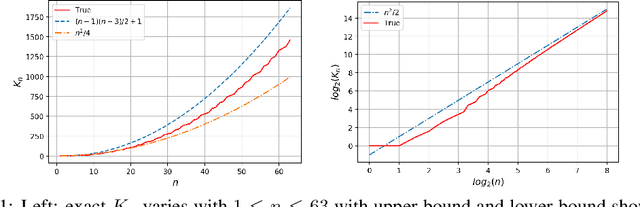
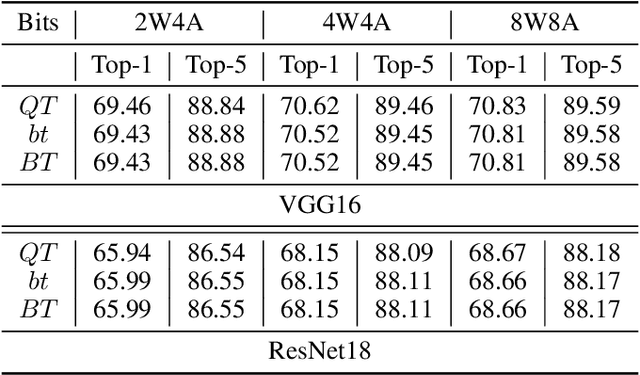
Quantized Neural Networks (QNNs) use low bit-width fixed-point numbers for representing weight parameters and activations, and are often used in real-world applications due to their saving of computation resources and reproducibility of results. Batch Normalization (BN) poses a challenge for QNNs for requiring floating points in reciprocal operations, and previous QNNs either require computing BN at high precision or revise BN to some variants in heuristic ways. In this work, we propose a novel method to quantize BN by converting an affine transformation of two floating points to a fixed-point operation with shared quantized scale, which is friendly for hardware acceleration and model deployment. We confirm that our method maintains same outputs through rigorous theoretical analysis and numerical analysis. Accuracy and efficiency of our quantization method are verified by experiments at layer level on CIFAR and ImageNet datasets. We also believe that our method is potentially useful in other problems involving quantization.

Towards Understanding the Importance of Noise in Training Neural Networks

Numerous empirical evidence has corroborated that the noise plays a crucial rule in effective and efficient training of neural networks. The theory behind, however, is still largely unknown. This paper studies this fundamental problem through training a simple two-layer convolutional neural network model. Although training such a network requires solving a nonconvex optimization problem with a spurious local optimum and a global optimum, we prove that perturbed gradient descent and perturbed mini-batch stochastic gradient algorithms in conjunction with noise annealing is guaranteed to converge to a global optimum in polynomial time with arbitrary initialization. This implies that the noise enables the algorithm to efficiently escape from the spurious local optimum. Numerical experiments are provided to support our theory.

Towards Better Generalization: BP-SVRG in Training Deep Neural Networks

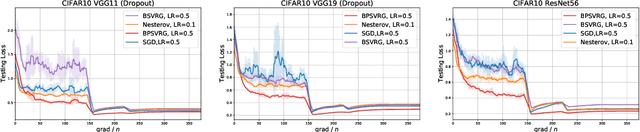
Stochastic variance-reduced gradient (SVRG) is a classical optimization method. Although it is theoretically proved to have better convergence performance than stochastic gradient descent (SGD), the generalization performance of SVRG remains open. In this paper we investigate the effects of some training techniques, mini-batching and learning rate decay, on the generalization performance of SVRG, and verify the generalization performance of Batch-SVRG (B-SVRG). In terms of the relationship between optimization and generalization, we believe that the average norm of gradients on each training sample as well as the norm of average gradient indicate how flat the landscape is and how well the model generalizes. Based on empirical observations of such metrics, we perform a sign switch on B-SVRG and derive a practical algorithm, BatchPlus-SVRG (BP-SVRG), which is numerically shown to enjoy better generalization performance than B-SVRG, even SGD in some scenarios of deep neural networks.