Does 1/2-Tsallis-INF Also Work Well for Best-Arm Identification?

Regret minimization (RM) and best-arm identification (BAI) are two fundamental objectives in multi-armed bandits. Among regret-minimizing algorithms, $1/2$-Tsallis-INF is a canonical best-of-both-worlds FTRL algorithm: it achieves logarithmic pseudo-regret in stochastic bandits while retaining minimax-optimal regret in adversarial bandits, without knowing the environment in advance. This raises a natural question: can the same algorithm, without additional exploration, also identify the best arm reliably? We study this question in stochastic bandits by analyzing the failure probability $\operatorname{Err}_t$, defined as the probability that the empirical best arm determined by the cumulative importance-weighted loss estimates of 1/2-Tsallis-INF differs from the true optimal arm. The main difficulty is that, at the logarithmic-regret scale, suboptimal arms are sampled with probability heuristically of order $1/t$. Consequently, importance weighting causes the cumulative estimator to fluctuate on the same linear scale as its mean separation. To overcome this obstacle, guided by a diffusion toy model, we construct a Lyapunov function for the gap process between the estimated cumulative loss of the optimal arm and that of the best competing arm. This leads to polynomial upper bounds on $\operatorname{Err}_t$: for learning rate $η_t=α/\sqrt t$, $\operatorname{Err}_t$ decays at rate $t^{-2+α^2μ_{i_*}/4+ρ}$ for any $ρ>0$, where $μ_{i_*}$ denotes the mean loss of the true optimal arm. We also establish a lower bound $Ω(t^{-2-\varepsilon})$ for any $\varepsilon>0$, showing that the exponent $2$ is essentially tight.

Last Iterate Analyses of FTRL in Stochasitc Bandits

The convergence analysis of online learning algorithms is central to machine learning theory, where last-iterate convergence is particularly important, as it captures the learner's actual decisions and describes the evolution of the learning process over time. However, in multi-armed bandits, most existing algorithmic analyses mainly focus on the order of regret, while the last-iterate (simple regret) convergence rate remains less explored -- especially for the widely studied Follow-the-Regularized-Leader (FTRL) algorithms. Recently, a growing line of work has established the Best-of-Both-Worlds (BOBW) property of FTRL algorithms in bandit problems, showing in particular that they achieve logarithmic regret in stochastic bandits. Nevertheless, their last-iterate convergence rate has not yet been studied. Intuitively, logarithmic regret should correspond to a $t^{-1}$ last-iterate convergence rate. This paper partially confirms this intuition through theoretical analysis, showing that the Bregman divergence, defined by the regular function $\Psi(p)=-4\sum_{i=1}^{d}\sqrt{p_i}$ associated with the BOBW FTRL algorithm $1/2$-Tsallis-INF (arXiv:1807.07623), between the point mass on the optimal arm and the probability distribution over the arm set obtained at iteration $t$, decays at a rate of $t^{-1/2}$.

Decoupled Functional Central Limit Theorems for Two-Time-Scale Stochastic Approximation

In two-time-scale stochastic approximation (SA), two iterates are updated at different rates, governed by distinct step sizes, with each update influencing the other. Previous studies have demonstrated that the convergence rates of the error terms for these updates depend solely on their respective step sizes, a property known as decoupled convergence. However, a functional version of this decoupled convergence has not been explored. Our work fills this gap by establishing decoupled functional central limit theorems for two-time-scale SA, offering a more precise characterization of its asymptotic behavior. To achieve these results, we leverage the martingale problem approach and establish tightness as a crucial intermediate step. Furthermore, to address the interdependence between different time scales, we introduce an innovative auxiliary sequence to eliminate the primary influence of the fast-time-scale update on the slow-time-scale update.

Technique Report of CVPR 2024 PBDL Challenges

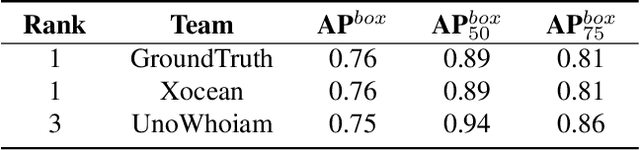
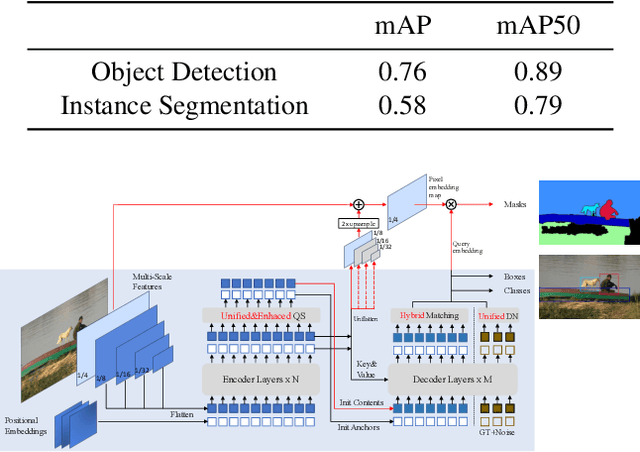
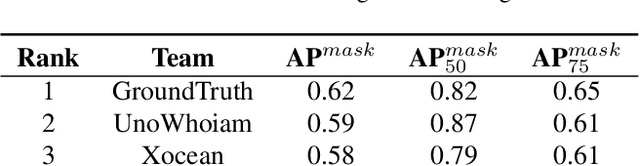
The intersection of physics-based vision and deep learning presents an exciting frontier for advancing computer vision technologies. By leveraging the principles of physics to inform and enhance deep learning models, we can develop more robust and accurate vision systems. Physics-based vision aims to invert the processes to recover scene properties such as shape, reflectance, light distribution, and medium properties from images. In recent years, deep learning has shown promising improvements for various vision tasks, and when combined with physics-based vision, these approaches can enhance the robustness and accuracy of vision systems. This technical report summarizes the outcomes of the Physics-Based Vision Meets Deep Learning (PBDL) 2024 challenge, held in CVPR 2024 workshop. The challenge consisted of eight tracks, focusing on Low-Light Enhancement and Detection as well as High Dynamic Range (HDR) Imaging. This report details the objectives, methodologies, and results of each track, highlighting the top-performing solutions and their innovative approaches.

Finite-Time Decoupled Convergence in Nonlinear Two-Time-Scale Stochastic Approximation

In two-time-scale stochastic approximation (SA), two iterates are updated at varying speeds using different step sizes, with each update influencing the other. Previous studies in linear two-time-scale SA have found that the convergence rates of the mean-square errors for these updates are dependent solely on their respective step sizes, leading to what is referred to as decoupled convergence. However, the possibility of achieving this decoupled convergence in nonlinear SA remains less understood. Our research explores the potential for finite-time decoupled convergence in nonlinear two-time-scale SA. We find that under a weaker Lipschitz condition, traditional analyses are insufficient for achieving decoupled convergence. This finding is further numerically supported by a counterexample. But by introducing an additional condition of nested local linearity, we show that decoupled convergence is still feasible, contingent on the appropriate choice of step sizes associated with smoothness parameters. Our analysis depends on a refined characterization of the matrix cross term between the two iterates and utilizes fourth-order moments to control higher-order approximation errors induced by the local linearity assumption.

Asymptotic Behaviors and Phase Transitions in Projected Stochastic Approximation: A Jump Diffusion Approach

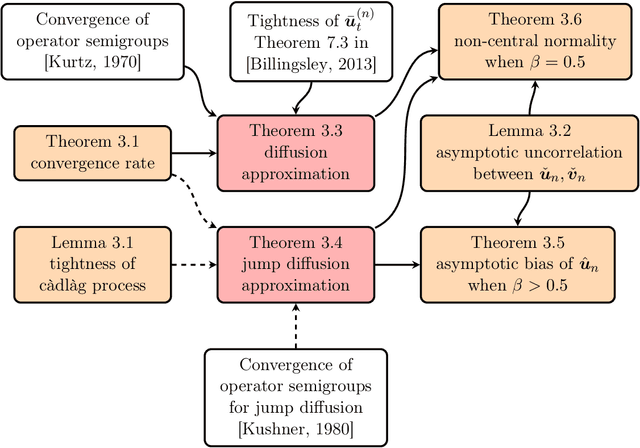
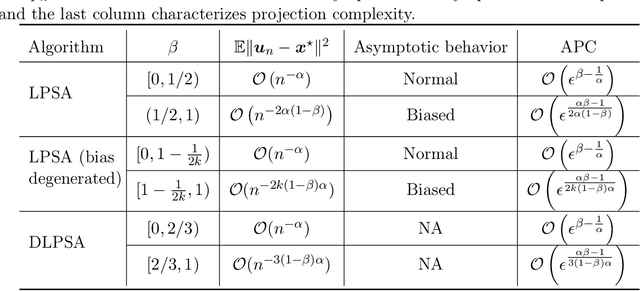
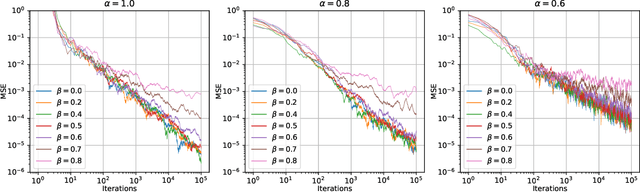
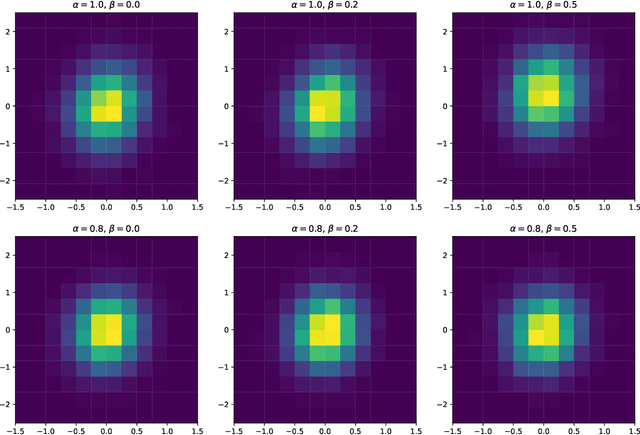
In this paper we consider linearly constrained optimization problems and propose a loopless projection stochastic approximation (LPSA) algorithm. It performs the projection with probability $p_n$ at the $n$-th iteration to ensure feasibility. Considering a specific family of the probability $p_n$ and step size $\eta_n$, we analyze our algorithm from an asymptotic and continuous perspective. Using a novel jump diffusion approximation, we show that the trajectories connecting those properly rescaled last iterates weakly converge to the solution of specific stochastic differential equations (SDEs). By analyzing SDEs, we identify the asymptotic behaviors of LPSA for different choices of $(p_n, \eta_n)$. We find that the algorithm presents an intriguing asymptotic bias-variance trade-off and yields phase transition phenomenons, according to the relative magnitude of $p_n$ w.r.t. $\eta_n$. This finding provides insights on selecting appropriate ${(p_n, \eta_n)}_{n \geq 1}$ to minimize the projection cost. Additionally, we propose the Debiased LPSA (DLPSA) as a practical application of our jump diffusion approximation result. DLPSA is shown to effectively reduce projection complexity compared to vanilla LPSA.

Stochastic Distributed Optimization under Average Second-order Similarity: Algorithms and Analysis

We study finite-sum distributed optimization problems with $n$-clients under popular $\delta$-similarity condition and $\mu$-strong convexity. We propose two new algorithms: SVRS and AccSVRS motivated by previous works. The non-accelerated SVRS method combines the techniques of gradient-sliding and variance reduction, which achieves superior communication complexity $\tilde{\gO}(n {+} \sqrt{n}\delta/\mu)$ compared to existing non-accelerated algorithms. Applying the framework proposed in Katyusha X, we also build a direct accelerated practical version named AccSVRS with totally smoothness-free $\tilde{\gO}(n {+} n^{3/4}\sqrt{\delta/\mu})$ communication complexity that improves upon existing algorithms on ill-conditioning cases. Furthermore, we show a nearly matched lower bound to verify the tightness of our AccSVRS method.

Lower Complexity Bounds of Finite-Sum Optimization Problems: The Results and Construction

The contribution of this paper includes two aspects. First, we study the lower bound complexity for the minimax optimization problem whose objective function is the average of $n$ individual smooth component functions. We consider Proximal Incremental First-order (PIFO) algorithms which have access to gradient and proximal oracle for each individual component. We develop a novel approach for constructing adversarial problems, which partitions the tridiagonal matrix of classical examples into $n$ groups. This construction is friendly to the analysis of incremental gradient and proximal oracle. With this approach, we demonstrate the lower bounds of first-order algorithms for finding an $\varepsilon$-suboptimal point and an $\varepsilon$-stationary point in different settings. Second, we also derive the lower bounds of minimization optimization with PIFO algorithms from our approach, which can cover the results in \citep{woodworth2016tight} and improve the results in \citep{zhou2019lower}.

DIPPA: An improved Method for Bilinear Saddle Point Problems

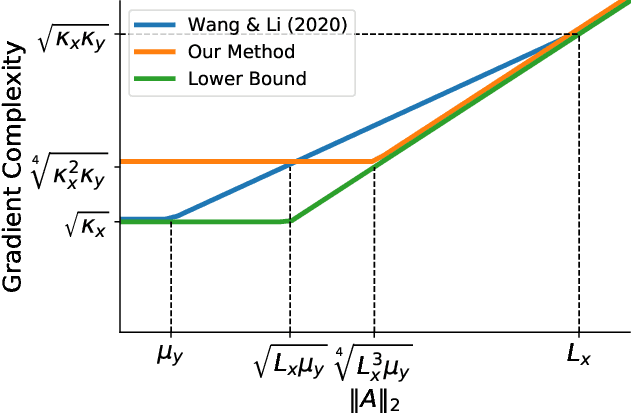
This paper studies bilinear saddle point problems $\min_{\bf{x}} \max_{\bf{y}} g(\bf{x}) + \bf{x}^{\top} \bf{A} \bf{y} - h(\bf{y})$, where the functions $g, h$ are smooth and strongly-convex. When the gradient and proximal oracle related to $g$ and $h$ are accessible, optimal algorithms have already been developed in the literature \cite{chambolle2011first, palaniappan2016stochastic}. However, the proximal operator is not always easy to compute, especially in constraint zero-sum matrix games \cite{zhang2020sparsified}. This work proposes a new algorithm which only requires the access to the gradients of $g, h$. Our algorithm achieves a complexity upper bound $\tilde{\mathcal{O}}\left( \frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}} + \sqrt[4]{\kappa_x \kappa_y (\kappa_x + \kappa_y)} \right)$ which has optimal dependency on the coupling condition number $\frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}}$ up to logarithmic factors.