Near Optimal Stochastic Algorithms for Finite-Sum Unbalanced Convex-Concave Minimax Optimization

This paper considers stochastic first-order algorithms for convex-concave minimax problems of the form $\min_{\bf x}\max_{\bf y}f(\bf x, \bf y)$, where $f$ can be presented by the average of $n$ individual components which are $L$-average smooth. For $\mu_x$-strongly-convex-$\mu_y$-strongly-concave setting, we propose a new method which could find a $\varepsilon$-saddle point of the problem in $\tilde{\mathcal O} \big(\sqrt{n(\sqrt{n}+\kappa_x)(\sqrt{n}+\kappa_y)}\log(1/\varepsilon)\big)$ stochastic first-order complexity, where $\kappa_x\triangleq L/\mu_x$ and $\kappa_y\triangleq L/\mu_y$. This upper bound is near optimal with respect to $\varepsilon$, $n$, $\kappa_x$ and $\kappa_y$ simultaneously. In addition, the algorithm is easily implemented and works well in practical. Our methods can be extended to solve more general unbalanced convex-concave minimax problems and the corresponding upper complexity bounds are also near optimal.

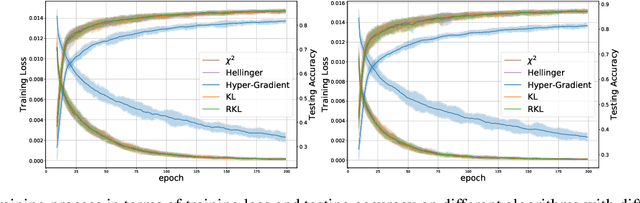
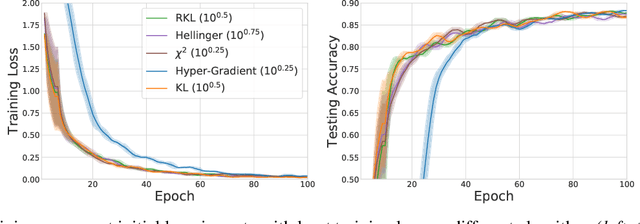
Meta-Regularization: An Approach to Adaptive Choice of the Learning Rate in Gradient Descent

We propose \textit{Meta-Regularization}, a novel approach for the adaptive choice of the learning rate in first-order gradient descent methods. Our approach modifies the objective function by adding a regularization term on the learning rate, and casts the joint updating process of parameters and learning rates into a maxmin problem. Given any regularization term, our approach facilitates the generation of practical algorithms. When \textit{Meta-Regularization} takes the $\varphi$-divergence as a regularizer, the resulting algorithms exhibit comparable theoretical convergence performance with other first-order gradient-based algorithms. Furthermore, we theoretically prove that some well-designed regularizers can improve the convergence performance under the strong-convexity condition of the objective function. Numerical experiments on benchmark problems demonstrate the effectiveness of algorithms derived from some common $\varphi$-divergence in full batch as well as online learning settings.

Lower Complexity Bounds of Finite-Sum Optimization Problems: The Results and Construction

The contribution of this paper includes two aspects. First, we study the lower bound complexity for the minimax optimization problem whose objective function is the average of $n$ individual smooth component functions. We consider Proximal Incremental First-order (PIFO) algorithms which have access to gradient and proximal oracle for each individual component. We develop a novel approach for constructing adversarial problems, which partitions the tridiagonal matrix of classical examples into $n$ groups. This construction is friendly to the analysis of incremental gradient and proximal oracle. With this approach, we demonstrate the lower bounds of first-order algorithms for finding an $\varepsilon$-suboptimal point and an $\varepsilon$-stationary point in different settings. Second, we also derive the lower bounds of minimization optimization with PIFO algorithms from our approach, which can cover the results in \citep{woodworth2016tight} and improve the results in \citep{zhou2019lower}.

DIPPA: An improved Method for Bilinear Saddle Point Problems

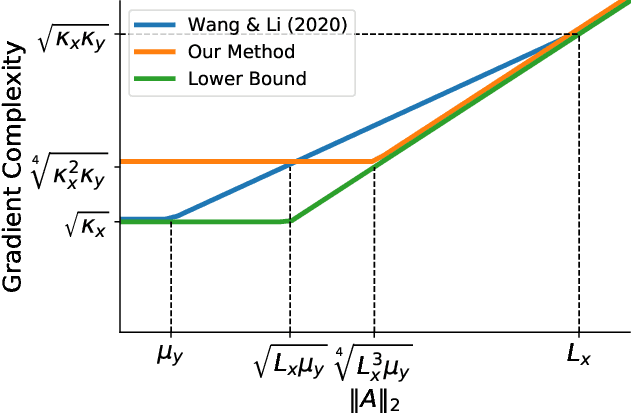
This paper studies bilinear saddle point problems $\min_{\bf{x}} \max_{\bf{y}} g(\bf{x}) + \bf{x}^{\top} \bf{A} \bf{y} - h(\bf{y})$, where the functions $g, h$ are smooth and strongly-convex. When the gradient and proximal oracle related to $g$ and $h$ are accessible, optimal algorithms have already been developed in the literature \cite{chambolle2011first, palaniappan2016stochastic}. However, the proximal operator is not always easy to compute, especially in constraint zero-sum matrix games \cite{zhang2020sparsified}. This work proposes a new algorithm which only requires the access to the gradients of $g, h$. Our algorithm achieves a complexity upper bound $\tilde{\mathcal{O}}\left( \frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}} + \sqrt[4]{\kappa_x \kappa_y (\kappa_x + \kappa_y)} \right)$ which has optimal dependency on the coupling condition number $\frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}}$ up to logarithmic factors.

Finding the Near Optimal Policy via Adaptive Reduced Regularization in MDPs

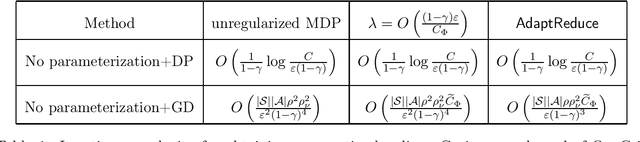
Regularized MDPs serve as a smooth version of original MDPs. However, biased optimal policy always exists for regularized MDPs. Instead of making the coefficient{\lambda}of regularized term sufficiently small, we propose an adaptive reduction scheme for {\lambda} to approximate optimal policy of the original MDP. It is shown that the iteration complexity for obtaining an{\epsilon}-optimal policy could be reduced in comparison with setting sufficiently small{\lambda}. In addition, there exists strong duality connection between the reduction method and solving the original MDP directly, from which we can derive more adaptive reduction method for certain algorithms.

Revisiting Co-Occurring Directions: Sharper Analysis and Efficient Algorithm for Sparse Matrices

We study the streaming model for approximate matrix multiplication (AMM). We are interested in the scenario that the algorithm can only take one pass over the data with limited memory. The state-of-the-art deterministic sketching algorithm for streaming AMM is the co-occurring directions (COD), which has much smaller approximation errors than randomized algorithms and outperforms other deterministic sketching methods empirically. In this paper, we provide a tighter error bound for COD whose leading term considers the potential approximate low-rank structure and the correlation of input matrices. We prove COD is space optimal with respect to our improved error bound. We also propose a variant of COD for sparse matrices with theoretical guarantees. The experiments on real-world sparse datasets show that the proposed algorithm is more efficient than baseline methods.

Optimal Quantization for Batch Normalization in Neural Network Deployments and Beyond

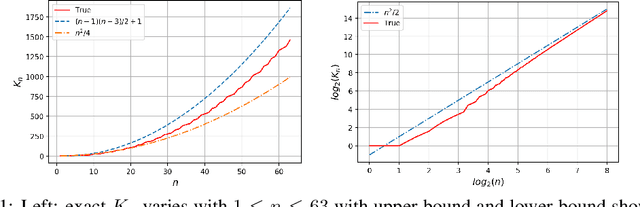
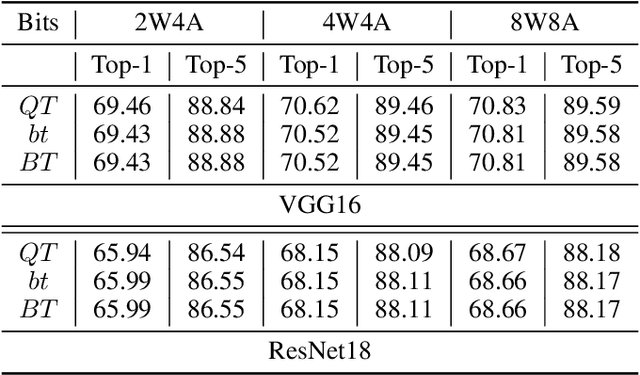
Quantized Neural Networks (QNNs) use low bit-width fixed-point numbers for representing weight parameters and activations, and are often used in real-world applications due to their saving of computation resources and reproducibility of results. Batch Normalization (BN) poses a challenge for QNNs for requiring floating points in reciprocal operations, and previous QNNs either require computing BN at high precision or revise BN to some variants in heuristic ways. In this work, we propose a novel method to quantize BN by converting an affine transformation of two floating points to a fixed-point operation with shared quantized scale, which is friendly for hardware acceleration and model deployment. We confirm that our method maintains same outputs through rigorous theoretical analysis and numerical analysis. Accuracy and efficiency of our quantization method are verified by experiments at layer level on CIFAR and ImageNet datasets. We also believe that our method is potentially useful in other problems involving quantization.

A Stochastic Proximal Point Algorithm for Saddle-Point Problems

We consider saddle point problems which objective functions are the average of $n$ strongly convex-concave individual components. Recently, researchers exploit variance reduction methods to solve such problems and achieve linear-convergence guarantees. However, these methods have a slow convergence when the condition number of the problem is very large. In this paper, we propose a stochastic proximal point algorithm, which accelerates the variance reduction method SAGA for saddle point problems. Compared with the catalyst framework, our algorithm reduces a logarithmic term of condition number for the iteration complexity. We adopt our algorithm to policy evaluation and the empirical results show that our method is much more efficient than state-of-the-art methods.

A General Analysis Framework of Lower Complexity Bounds for Finite-Sum Optimization

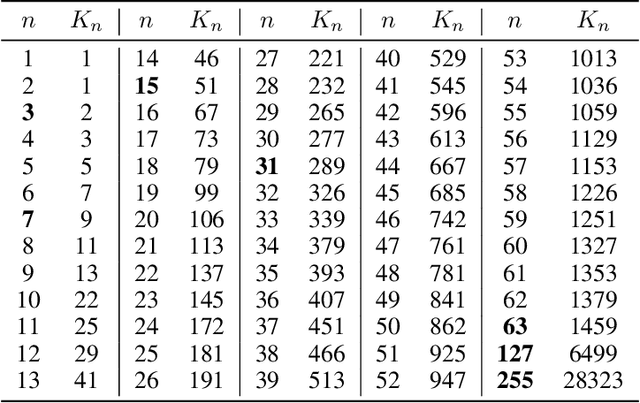
This paper studies the lower bound complexity for the optimization problem whose objective function is the average of $n$ individual smooth convex functions. We consider the algorithm which gets access to gradient and proximal oracle for each individual component. For the strongly-convex case, we prove such an algorithm can not reach an $\varepsilon$-suboptimal point in fewer than $\Omega((n+\sqrt{\kappa n})\log(1/\varepsilon))$ iterations, where $\kappa$ is the condition number of the objective function. This lower bound is tighter than previous results and perfectly matches the upper bound of the existing proximal incremental first-order oracle algorithm Point-SAGA. We develop a novel construction to show the above result, which partitions the tridiagonal matrix of classical examples into $n$ groups. This construction is friendly to the analysis of proximal oracle and also could be used to general convex and average smooth cases naturally.

Interpolatron: Interpolation or Extrapolation Schemes to Accelerate Optimization for Deep Neural Networks

In this paper we explore acceleration techniques for large scale nonconvex optimization problems with special focuses on deep neural networks. The extrapolation scheme is a classical approach for accelerating stochastic gradient descent for convex optimization, but it does not work well for nonconvex optimization typically. Alternatively, we propose an interpolation scheme to accelerate nonconvex optimization and call the method Interpolatron. We explain motivation behind Interpolatron and conduct a thorough empirical analysis. Empirical results on DNNs of great depths (e.g., 98-layer ResNet and 200-layer ResNet) on CIFAR-10 and ImageNet show that Interpolatron can converge much faster than the state-of-the-art methods such as the SGD with momentum and Adam. Furthermore, Anderson's acceleration, in which mixing coefficients are computed by least-squares estimation, can also be used to improve the performance. Both Interpolatron and Anderson's acceleration are easy to implement and tune. We also show that Interpolatron has linear convergence rate under certain regularity assumptions.