Meta-Regularization: An Approach to Adaptive Choice of the Learning Rate in Gradient Descent
Paper and Code
Apr 12, 2021
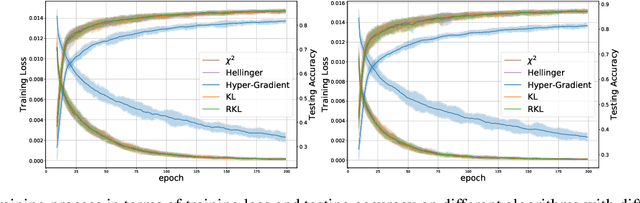
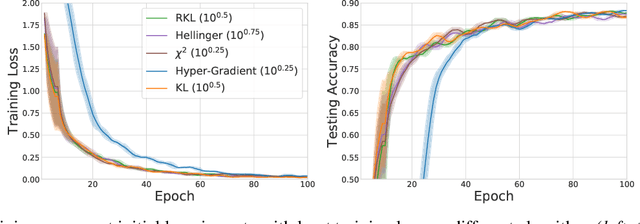

We propose \textit{Meta-Regularization}, a novel approach for the adaptive choice of the learning rate in first-order gradient descent methods. Our approach modifies the objective function by adding a regularization term on the learning rate, and casts the joint updating process of parameters and learning rates into a maxmin problem. Given any regularization term, our approach facilitates the generation of practical algorithms. When \textit{Meta-Regularization} takes the $\varphi$-divergence as a regularizer, the resulting algorithms exhibit comparable theoretical convergence performance with other first-order gradient-based algorithms. Furthermore, we theoretically prove that some well-designed regularizers can improve the convergence performance under the strong-convexity condition of the objective function. Numerical experiments on benchmark problems demonstrate the effectiveness of algorithms derived from some common $\varphi$-divergence in full batch as well as online learning settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge