Universality of General Spiked Tensor Models

We study the rank-one spiked tensor model in the high-dimensional regime, where the noise entries are independent and identically distributed with zero mean, unit variance, and finite fourth moment.This setting extends the classical Gaussian framework to a substantially broader class of noise distributions.Focusing on asymmetric tensors of order $d$ ($\ge 3$), we analyze the maximum likelihood estimator of the best rank-one approximation.Under a mild assumption isolating informative critical points of the associated optimization landscape, we show that the empirical spectral distribution of a suitably defined block-wise tensor contraction converges almost surely to a deterministic limit that coincides with the Gaussian case.As a consequence, the asymptotic singular value and the alignments between the estimated and true spike directions admit explicit characterizations identical to those obtained under Gaussian noise. These results establish a universality principle for spiked tensor models, demonstrating that their high-dimensional spectral behavior and statistical limits are robust to non-Gaussian noise. Our analysis relies on resolvent methods from random matrix theory, cumulant expansions valid under finite moment assumptions, and variance bounds based on Efron-Stein-type arguments. A key challenge in the proof is how to handle the statistical dependence between the signal term and the noise term.

Accelerated Distributional Temporal Difference Learning with Linear Function Approximation

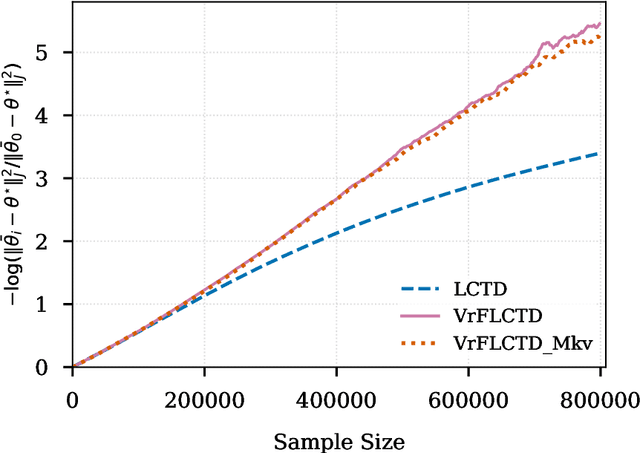
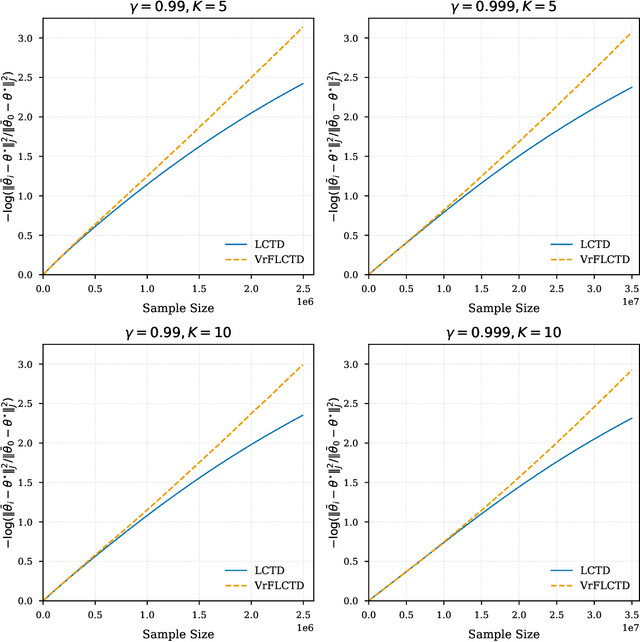
In this paper, we study the finite-sample statistical rates of distributional temporal difference (TD) learning with linear function approximation. The purpose of distributional TD learning is to estimate the return distribution of a discounted Markov decision process for a given policy. Previous works on statistical analysis of distributional TD learning focus mainly on the tabular case. We first consider the linear function approximation setting and conduct a fine-grained analysis of the linear-categorical Bellman equation. Building on this analysis, we further incorporate variance reduction techniques in our new algorithms to establish tight sample complexity bounds independent of the support size $K$ when $K$ is large. Our theoretical results imply that, when employing distributional TD learning with linear function approximation, learning the full distribution of the return function from streaming data is no more difficult than learning its expectation. This work provide new insights into the statistical efficiency of distributional reinforcement learning algorithms.

CAST-LUT: Tokenizer-Guided HSV Look-Up Tables for Purple Flare Removal

Purple flare, a diffuse chromatic aberration artifact commonly found around highlight areas, severely degrades the tone transition and color of the image. Existing traditional methods are based on hand-crafted features, which lack flexibility and rely entirely on fixed priors, while the scarcity of paired training data critically hampers deep learning. To address this issue, we propose a novel network built upon decoupled HSV Look-Up Tables (LUTs). The method aims to simplify color correction by adjusting the Hue (H), Saturation (S), and Value (V) components independently. This approach resolves the inherent color coupling problems in traditional methods. Our model adopts a two-stage architecture: First, a Chroma-Aware Spectral Tokenizer (CAST) converts the input image from RGB space to HSV space and independently encodes the Hue (H) and Value (V) channels into a set of semantic tokens describing the Purple flare status; second, the HSV-LUT module takes these tokens as input and dynamically generates independent correction curves (1D-LUTs) for the three channels H, S, and V. To effectively train and validate our model, we built the first large-scale purple flare dataset with diverse scenes. We also proposed new metrics and a loss function specifically designed for this task. Extensive experiments demonstrate that our model not only significantly outperforms existing methods in visual effects but also achieves state-of-the-art performance on all quantitative metrics.

Last Iterate Analyses of FTRL in Stochasitc Bandits

The convergence analysis of online learning algorithms is central to machine learning theory, where last-iterate convergence is particularly important, as it captures the learner's actual decisions and describes the evolution of the learning process over time. However, in multi-armed bandits, most existing algorithmic analyses mainly focus on the order of regret, while the last-iterate (simple regret) convergence rate remains less explored -- especially for the widely studied Follow-the-Regularized-Leader (FTRL) algorithms. Recently, a growing line of work has established the Best-of-Both-Worlds (BOBW) property of FTRL algorithms in bandit problems, showing in particular that they achieve logarithmic regret in stochastic bandits. Nevertheless, their last-iterate convergence rate has not yet been studied. Intuitively, logarithmic regret should correspond to a $t^{-1}$ last-iterate convergence rate. This paper partially confirms this intuition through theoretical analysis, showing that the Bregman divergence, defined by the regular function $\Psi(p)=-4\sum_{i=1}^{d}\sqrt{p_i}$ associated with the BOBW FTRL algorithm $1/2$-Tsallis-INF (arXiv:1807.07623), between the point mass on the optimal arm and the probability distribution over the arm set obtained at iteration $t$, decays at a rate of $t^{-1/2}$.

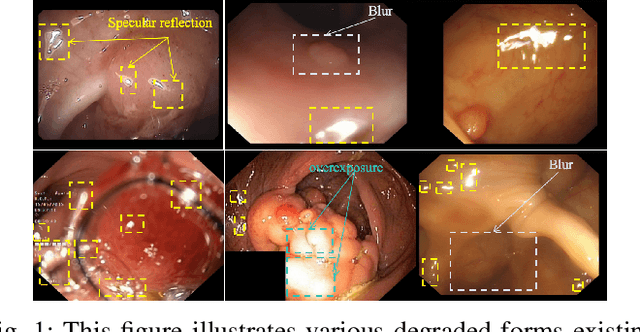
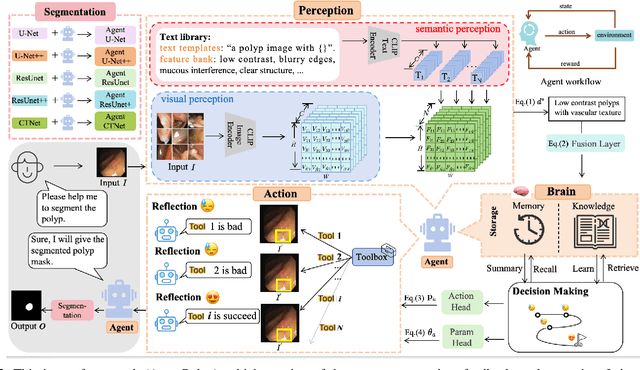
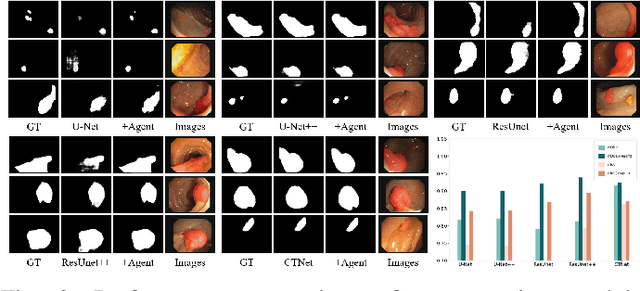
AgentPolyp: Accurate Polyp Segmentation via Image Enhancement Agent

Since human and environmental factors interfere, captured polyp images usually suffer from issues such as dim lighting, blur, and overexposure, which pose challenges for downstream polyp segmentation tasks. To address the challenges of noise-induced degradation in polyp images, we present AgentPolyp, a novel framework integrating CLIP-based semantic guidance and dynamic image enhancement with a lightweight neural network for segmentation. The agent first evaluates image quality using CLIP-driven semantic analysis (e.g., identifying ``low-contrast polyps with vascular textures") and adapts reinforcement learning strategies to dynamically apply multi-modal enhancement operations (e.g., denoising, contrast adjustment). A quality assessment feedback loop optimizes pixel-level enhancement and segmentation focus in a collaborative manner, ensuring robust preprocessing before neural network segmentation. This modular architecture supports plug-and-play extensions for various enhancement algorithms and segmentation networks, meeting deployment requirements for endoscopic devices.

Follow-the-Perturbed-Leader Achieves Best-of-Both-Worlds for the m-Set Semi-Bandit Problems

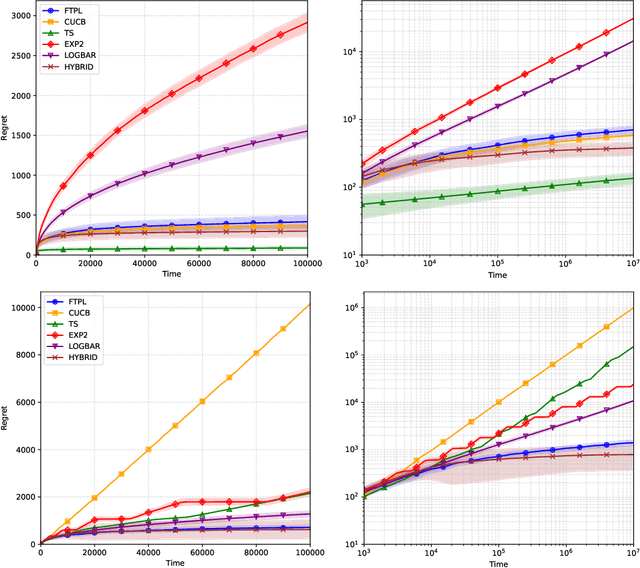
We consider a common case of the combinatorial semi-bandit problem, the $m$-set semi-bandit, where the learner exactly selects $m$ arms from the total $d$ arms. In the adversarial setting, the best regret bound, known to be $\mathcal{O}(\sqrt{nmd})$ for time horizon $n$, is achieved by the well-known Follow-the-Regularized-Leader (FTRL) policy, which, however, requires to explicitly compute the arm-selection probabilities by solving optimizing problems at each time step and sample according to it. This problem can be avoided by the Follow-the-Perturbed-Leader (FTPL) policy, which simply pulls the $m$ arms that rank among the $m$ smallest (estimated) loss with random perturbation. In this paper, we show that FTPL with a Fr\'echet perturbation also enjoys the optimal regret bound $\mathcal{O}(\sqrt{nmd})$ in the adversarial setting and achieves best-of-both-world regret bounds, i.e., achieves a logarithmic regret for the stochastic setting.

PolypFlow: Reinforcing Polyp Segmentation with Flow-Driven Dynamics

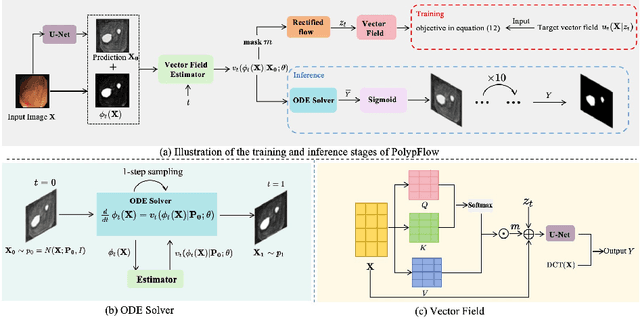
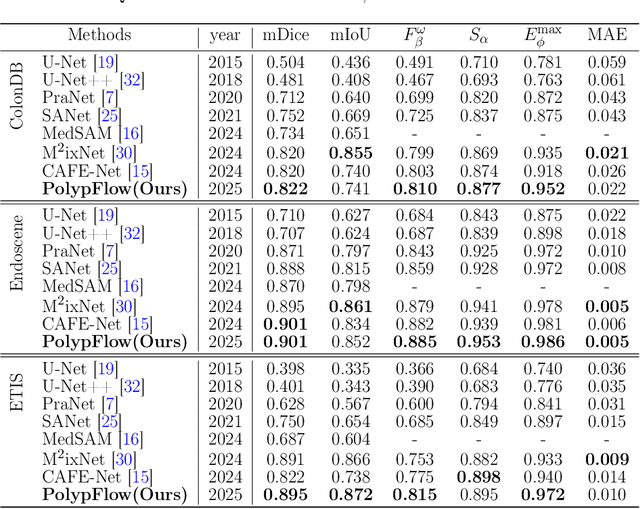
Accurate polyp segmentation remains challenging due to irregular lesion morphologies, ambiguous boundaries, and heterogeneous imaging conditions. While U-Net variants excel at local feature fusion, they often lack explicit mechanisms to model the dynamic evolution of segmentation confidence under uncertainty. Inspired by the interpretable nature of flow-based models, we present \textbf{PolypFLow}, a flow-matching enhanced architecture that injects physics-inspired optimization dynamics into segmentation refinement. Unlike conventional cascaded networks, our framework solves an ordinary differential equation (ODE) to progressively align coarse initial predictions with ground truth masks through learned velocity fields. This trajectory-based refinement offers two key advantages: 1) Interpretable Optimization: Intermediate flow steps visualize how the model corrects under-segmented regions and sharpens boundaries at each ODE-solver iteration, demystifying the ``black-box" refinement process; 2) Boundary-Aware Robustness: The flow dynamics explicitly model gradient directions along polyp edges, enhancing resilience to low-contrast regions and motion artifacts. Numerous experimental results show that PolypFLow achieves a state-of-the-art while maintaining consistent performance in different lighting scenarios.

Finite Sample Analysis of Distributional TD Learning with Linear Function Approximation

In this paper, we investigate the finite-sample statistical rates of distributional temporal difference (TD) learning with linear function approximation. The aim of distributional TD learning is to estimate the return distribution of a discounted Markov decision process for a given policy {\pi}. Prior works on statistical analysis of distributional TD learning mainly focus on the tabular case. In contrast, we first consider the linear function approximation setting and derive sharp finite-sample rates. Our theoretical results demonstrate that the sample complexity of linear distributional TD learning matches that of the classic linear TD learning. This implies that, with linear function approximation, learning the full distribution of the return using streaming data is no more difficult than learning its expectation (i.e. the value function). To derive tight sample complexity bounds, we conduct a fine-grained analysis of the linear-categorical Bellman equation, and employ the exponential stability arguments for products of random matrices. Our findings provide new insights into the statistical efficiency of distributional reinforcement learning algorithms.

A Regularized Online Newton Method for Stochastic Convex Bandits with Linear Vanishing Noise

We study a stochastic convex bandit problem where the subgaussian noise parameter is assumed to decrease linearly as the learner selects actions closer and closer to the minimizer of the convex loss function. Accordingly, we propose a Regularized Online Newton Method (RONM) for solving the problem, based on the Online Newton Method (ONM) of arXiv:2406.06506. Our RONM reaches a polylogarithmic regret in the time horizon $n$ when the loss function grows quadratically in the constraint set, which recovers the results of arXiv:2402.12042 in linear bandits. Our analyses rely on the growth rate of the precision matrix $\Sigma_t^{-1}$ in ONM and we find that linear growth solves the question exactly. These analyses also help us obtain better convergence rates when the loss function grows faster. We also study and analyze two new bandit models: stochastic convex bandits with noise scaled to a subgaussian parameter function and convex bandits with stochastic multiplicative noise.

Decoupled Functional Central Limit Theorems for Two-Time-Scale Stochastic Approximation

In two-time-scale stochastic approximation (SA), two iterates are updated at different rates, governed by distinct step sizes, with each update influencing the other. Previous studies have demonstrated that the convergence rates of the error terms for these updates depend solely on their respective step sizes, a property known as decoupled convergence. However, a functional version of this decoupled convergence has not been explored. Our work fills this gap by establishing decoupled functional central limit theorems for two-time-scale SA, offering a more precise characterization of its asymptotic behavior. To achieve these results, we leverage the martingale problem approach and establish tightness as a crucial intermediate step. Furthermore, to address the interdependence between different time scales, we introduce an innovative auxiliary sequence to eliminate the primary influence of the fast-time-scale update on the slow-time-scale update.