Federated Control in Markov Decision Processes
Paper and Code
May 07, 2024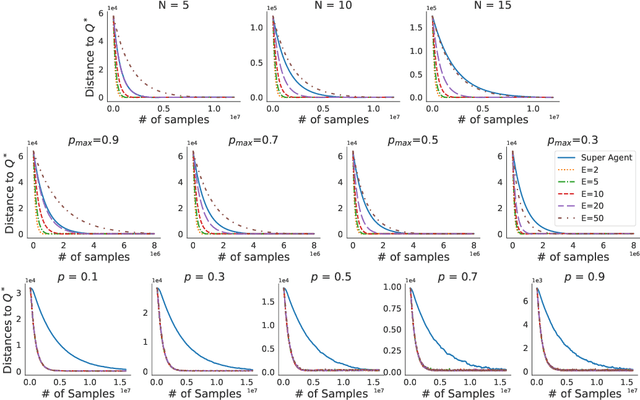
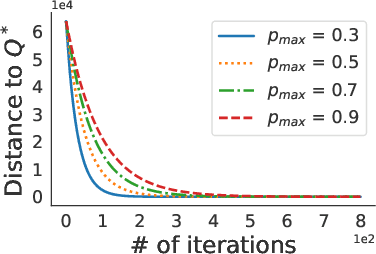
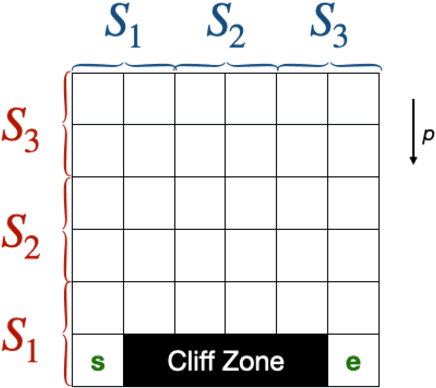
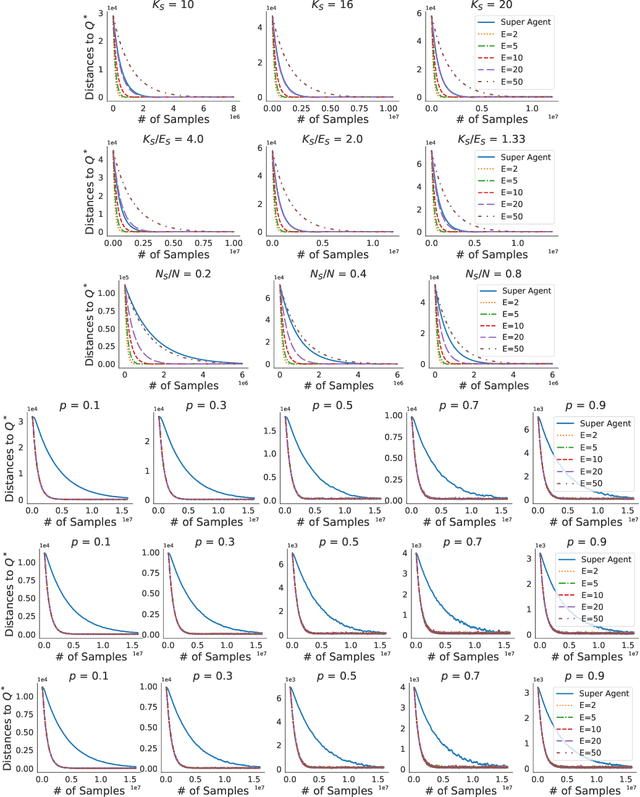
We study problems of federated control in Markov Decision Processes. To solve an MDP with large state space, multiple learning agents are introduced to collaboratively learn its optimal policy without communication of locally collected experience. In our settings, these agents have limited capabilities, which means they are restricted within different regions of the overall state space during the training process. In face of the difference among restricted regions, we firstly introduce concepts of leakage probabilities to understand how such heterogeneity affects the learning process, and then propose a novel communication protocol that we call Federated-Q protocol (FedQ), which periodically aggregates agents' knowledge of their restricted regions and accordingly modifies their learning problems for further training. In terms of theoretical analysis, we justify the correctness of FedQ as a communication protocol, then give a general result on sample complexity of derived algorithms FedQ-X with the RL oracle , and finally conduct a thorough study on the sample complexity of FedQ-SynQ. Specifically, FedQ-X has been shown to enjoy linear speedup in terms of sample complexity when workload is uniformly distributed among agents. Moreover, we carry out experiments in various environments to justify the efficiency of our methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge