Finite Sample Analysis of Distributional TD Learning with Linear Function Approximation

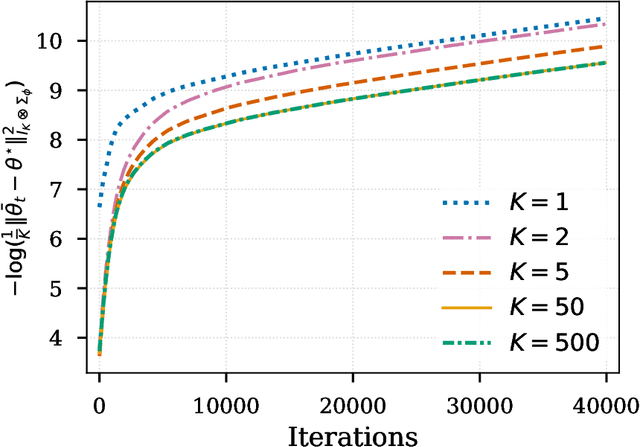
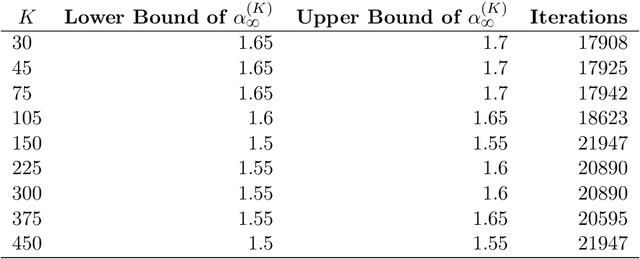
In this paper, we investigate the finite-sample statistical rates of distributional temporal difference (TD) learning with linear function approximation. The aim of distributional TD learning is to estimate the return distribution of a discounted Markov decision process for a given policy {\pi}. Prior works on statistical analysis of distributional TD learning mainly focus on the tabular case. In contrast, we first consider the linear function approximation setting and derive sharp finite-sample rates. Our theoretical results demonstrate that the sample complexity of linear distributional TD learning matches that of the classic linear TD learning. This implies that, with linear function approximation, learning the full distribution of the return using streaming data is no more difficult than learning its expectation (i.e. the value function). To derive tight sample complexity bounds, we conduct a fine-grained analysis of the linear-categorical Bellman equation, and employ the exponential stability arguments for products of random matrices. Our findings provide new insights into the statistical efficiency of distributional reinforcement learning algorithms.

Federated Control in Markov Decision Processes

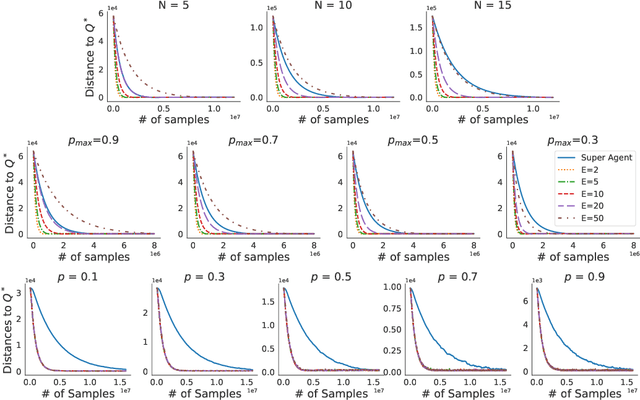
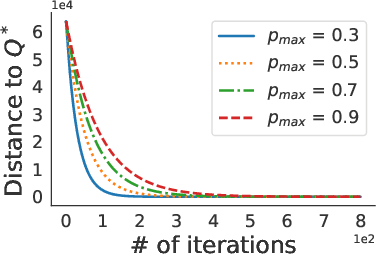
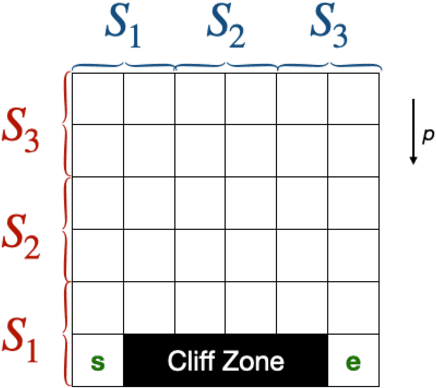
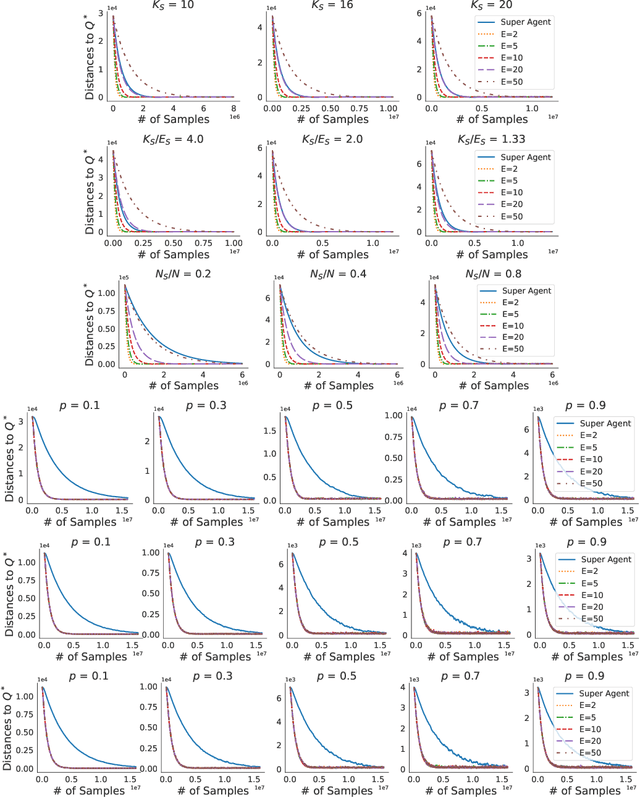
We study problems of federated control in Markov Decision Processes. To solve an MDP with large state space, multiple learning agents are introduced to collaboratively learn its optimal policy without communication of locally collected experience. In our settings, these agents have limited capabilities, which means they are restricted within different regions of the overall state space during the training process. In face of the difference among restricted regions, we firstly introduce concepts of leakage probabilities to understand how such heterogeneity affects the learning process, and then propose a novel communication protocol that we call Federated-Q protocol (FedQ), which periodically aggregates agents' knowledge of their restricted regions and accordingly modifies their learning problems for further training. In terms of theoretical analysis, we justify the correctness of FedQ as a communication protocol, then give a general result on sample complexity of derived algorithms FedQ-X with the RL oracle , and finally conduct a thorough study on the sample complexity of FedQ-SynQ. Specifically, FedQ-X has been shown to enjoy linear speedup in terms of sample complexity when workload is uniformly distributed among agents. Moreover, we carry out experiments in various environments to justify the efficiency of our methods.

Near Minimax-Optimal Distributional Temporal Difference Algorithms and The Freedman Inequality in Hilbert Spaces

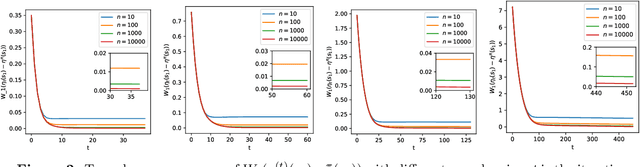
Distributional reinforcement learning (DRL) has achieved empirical success in various domains. One of the core tasks in the field of DRL is distributional policy evaluation, which involves estimating the return distribution $\eta^\pi$ for a given policy $\pi$. The distributional temporal difference (TD) algorithm has been accordingly proposed, which is an extension of the temporal difference algorithm in the classic RL literature. In the tabular case, \citet{rowland2018analysis} and \citet{rowland2023analysis} proved the asymptotic convergence of two instances of distributional TD, namely categorical temporal difference algorithm (CTD) and quantile temporal difference algorithm (QTD), respectively. In this paper, we go a step further and analyze the finite-sample performance of distributional TD. To facilitate theoretical analysis, we propose a non-parametric distributional TD algorithm (NTD). For a $\gamma$-discounted infinite-horizon tabular Markov decision process, we show that for NTD we need $\tilde{O}\left(\frac{1}{\varepsilon^{2p}(1-\gamma)^{2p+1}}\right)$ iterations to achieve an $\varepsilon$-optimal estimator with high probability, when the estimation error is measured by the $p$-Wasserstein distance. This sample complexity bound is minimax optimal (up to logarithmic factors) in the case of the $1$-Wasserstein distance. To achieve this, we establish a novel Freedman's inequality in Hilbert spaces, which would be of independent interest. In addition, we revisit CTD, showing that the same non-asymptotic convergence bounds hold for CTD in the case of the $p$-Wasserstein distance.

Estimation and Inference in Distributional Reinforcement Learning

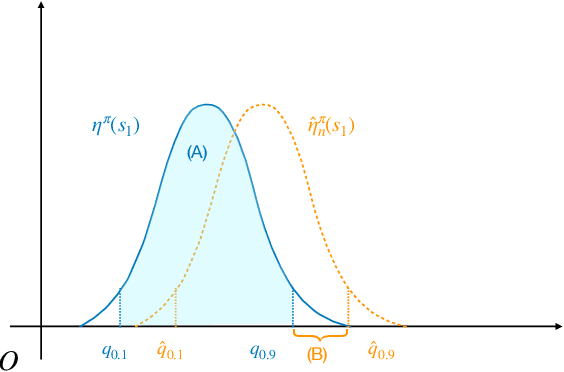
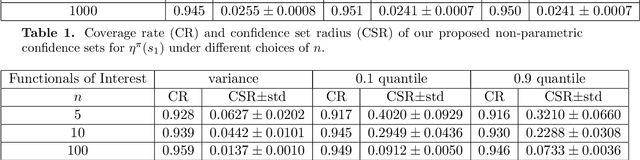
In this paper, we study distributional reinforcement learning from the perspective of statistical efficiency. We investigate distributional policy evaluation, aiming to estimate the complete distribution of the random return (denoted $\eta^\pi$) attained by a given policy $\pi$. We use the certainty-equivalence method to construct our estimator $\hat\eta^\pi$, given a generative model is available. We show that in this circumstance we need a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2p}(1-\gamma)^{2p+2}}\right)$ to guarantee a $p$-Wasserstein metric between $\hat\eta^\pi$ and $\eta^\pi$ is less than $\epsilon$ with high probability. This implies the distributional policy evaluation problem can be solved with sample efficiency. Also, we show that under different mild assumptions a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2}(1-\gamma)^{4}}\right)$ suffices to ensure the Kolmogorov metric and total variation metric between $\hat\eta^\pi$ and $\eta^\pi$ is below $\epsilon$ with high probability. Furthermore, we investigate the asymptotic behavior of $\hat\eta^\pi$. We demonstrate that the ``empirical process'' $\sqrt{n}(\hat\eta^\pi-\eta^\pi)$ converges weakly to a Gaussian process in the space of bounded functionals on Lipschitz function class $\ell^\infty(\mathcal{F}_{W_1})$, also in the space of bounded functionals on indicator function class $\ell^\infty(\mathcal{F}_{\mathrm{KS}})$ and bounded measurable function class $\ell^\infty(\mathcal{F}_{\mathrm{TV}})$ when some mild conditions hold. Our findings give rise to a unified approach to statistical inference of a wide class of statistical functionals of $\eta^\pi$.

Semi-Infinitely Constrained Markov Decision Processes and Efficient Reinforcement Learning

We propose a novel generalization of constrained Markov decision processes (CMDPs) that we call the \emph{semi-infinitely constrained Markov decision process} (SICMDP). Particularly, we consider a continuum of constraints instead of a finite number of constraints as in the case of ordinary CMDPs. We also devise two reinforcement learning algorithms for SICMDPs that we call SI-CRL and SI-CPO. SI-CRL is a model-based reinforcement learning algorithm. Given an estimate of the transition model, we first transform the reinforcement learning problem into a linear semi-infinitely programming (LSIP) problem and then use the dual exchange method in the LSIP literature to solve it. SI-CPO is a policy optimization algorithm. Borrowing the ideas from the cooperative stochastic approximation approach, we make alternative updates to the policy parameters to maximize the reward or minimize the cost. To the best of our knowledge, we are the first to apply tools from semi-infinitely programming (SIP) to solve constrained reinforcement learning problems. We present theoretical analysis for SI-CRL and SI-CPO, identifying their iteration complexity and sample complexity. We also conduct extensive numerical examples to illustrate the SICMDP model and demonstrate that our proposed algorithms are able to solve complex sequential decision-making tasks leveraging modern deep reinforcement learning techniques.

Statistical Estimation of Confounded Linear MDPs: An Instrumental Variable Approach

In an Markov decision process (MDP), unobservable confounders may exist and have impacts on the data generating process, so that the classic off-policy evaluation (OPE) estimators may fail to identify the true value function of the target policy. In this paper, we study the statistical properties of OPE in confounded MDPs with observable instrumental variables. Specifically, we propose a two-stage estimator based on the instrumental variables and establish its statistical properties in the confounded MDPs with a linear structure. For non-asymptotic analysis, we prove a $\mathcal{O}(n^{-1/2})$-error bound where $n$ is the number of samples. For asymptotic analysis, we prove that the two-stage estimator is asymptotically normal with a typical rate of $n^{1/2}$. To the best of our knowledge, we are the first to show such statistical results of the two-stage estimator for confounded linear MDPs via instrumental variables.

Intervention Generative Adversarial Networks

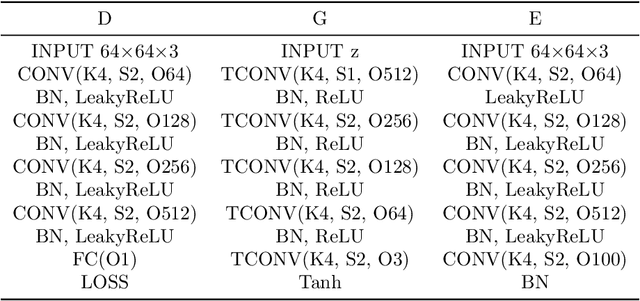
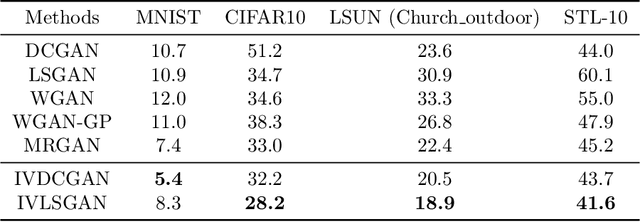
In this paper we propose a novel approach for stabilizing the training process of Generative Adversarial Networks as well as alleviating the mode collapse problem. The main idea is to introduce a regularization term that we call intervention loss into the objective. We refer to the resulting generative model as Intervention Generative Adversarial Networks (IVGAN). By perturbing the latent representations of real images obtained from an auxiliary encoder network with Gaussian invariant interventions and penalizing the dissimilarity of the distributions of the resulting generated images, the intervention loss provides more informative gradient for the generator, significantly improving GAN's training stability. We demonstrate the effectiveness and efficiency of our methods via solid theoretical analysis and thorough evaluation on standard real-world datasets as well as the stacked MNIST dataset.