Estimation and Inference in Distributional Reinforcement Learning
Paper and Code
Sep 29, 2023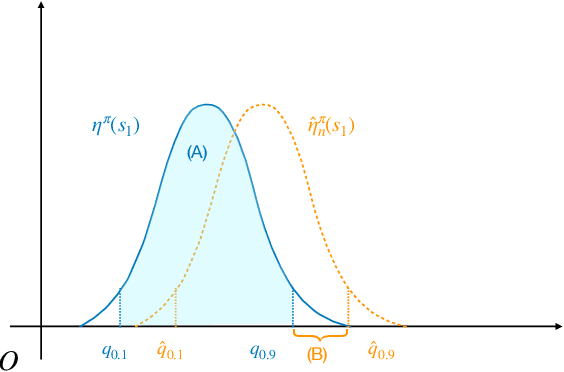

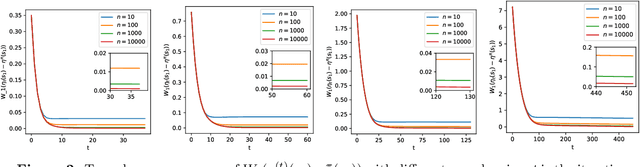
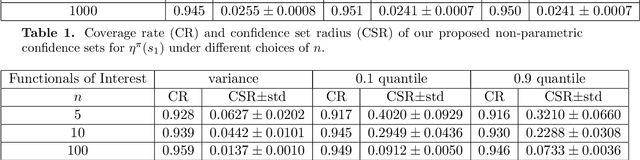
In this paper, we study distributional reinforcement learning from the perspective of statistical efficiency. We investigate distributional policy evaluation, aiming to estimate the complete distribution of the random return (denoted $\eta^\pi$) attained by a given policy $\pi$. We use the certainty-equivalence method to construct our estimator $\hat\eta^\pi$, given a generative model is available. We show that in this circumstance we need a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2p}(1-\gamma)^{2p+2}}\right)$ to guarantee a $p$-Wasserstein metric between $\hat\eta^\pi$ and $\eta^\pi$ is less than $\epsilon$ with high probability. This implies the distributional policy evaluation problem can be solved with sample efficiency. Also, we show that under different mild assumptions a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2}(1-\gamma)^{4}}\right)$ suffices to ensure the Kolmogorov metric and total variation metric between $\hat\eta^\pi$ and $\eta^\pi$ is below $\epsilon$ with high probability. Furthermore, we investigate the asymptotic behavior of $\hat\eta^\pi$. We demonstrate that the ``empirical process'' $\sqrt{n}(\hat\eta^\pi-\eta^\pi)$ converges weakly to a Gaussian process in the space of bounded functionals on Lipschitz function class $\ell^\infty(\mathcal{F}_{W_1})$, also in the space of bounded functionals on indicator function class $\ell^\infty(\mathcal{F}_{\mathrm{KS}})$ and bounded measurable function class $\ell^\infty(\mathcal{F}_{\mathrm{TV}})$ when some mild conditions hold. Our findings give rise to a unified approach to statistical inference of a wide class of statistical functionals of $\eta^\pi$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge