Asymptotic Time-Uniform Inference for Parameters in Averaged Stochastic Approximation

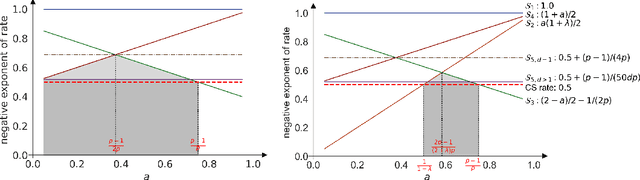
We study time-uniform statistical inference for parameters in stochastic approximation (SA), which encompasses a bunch of applications in optimization and machine learning. To that end, we analyze the almost-sure convergence rates of the averaged iterates to a scaled sum of Gaussians in both linear and nonlinear SA problems. We then construct three types of asymptotic confidence sequences that are valid uniformly across all times with coverage guarantees, in an asymptotic sense that the starting time is sufficiently large. These coverage guarantees remain valid if the unknown covariance matrix is replaced by its plug-in estimator, and we conduct experiments to validate our methodology.

Emotional Conversation: Empowering Talking Faces with Cohesive Expression, Gaze and Pose Generation

Vivid talking face generation holds immense potential applications across diverse multimedia domains, such as film and game production. While existing methods accurately synchronize lip movements with input audio, they typically ignore crucial alignments between emotion and facial cues, which include expression, gaze, and head pose. These alignments are indispensable for synthesizing realistic videos. To address these issues, we propose a two-stage audio-driven talking face generation framework that employs 3D facial landmarks as intermediate variables. This framework achieves collaborative alignment of expression, gaze, and pose with emotions through self-supervised learning. Specifically, we decompose this task into two key steps, namely speech-to-landmarks synthesis and landmarks-to-face generation. The first step focuses on simultaneously synthesizing emotionally aligned facial cues, including normalized landmarks that represent expressions, gaze, and head pose. These cues are subsequently reassembled into relocated facial landmarks. In the second step, these relocated landmarks are mapped to latent key points using self-supervised learning and then input into a pretrained model to create high-quality face images. Extensive experiments on the MEAD dataset demonstrate that our model significantly advances the state-of-the-art performance in both visual quality and emotional alignment.

Estimation and Inference in Distributional Reinforcement Learning

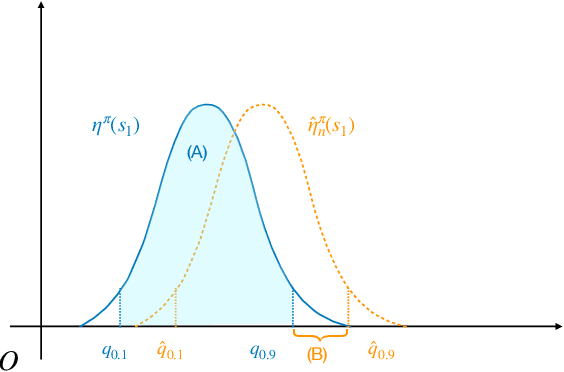
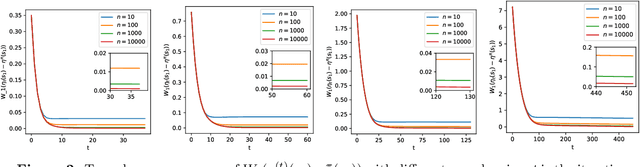
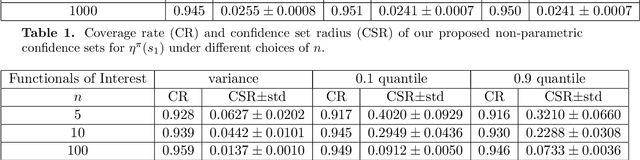
In this paper, we study distributional reinforcement learning from the perspective of statistical efficiency. We investigate distributional policy evaluation, aiming to estimate the complete distribution of the random return (denoted $\eta^\pi$) attained by a given policy $\pi$. We use the certainty-equivalence method to construct our estimator $\hat\eta^\pi$, given a generative model is available. We show that in this circumstance we need a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2p}(1-\gamma)^{2p+2}}\right)$ to guarantee a $p$-Wasserstein metric between $\hat\eta^\pi$ and $\eta^\pi$ is less than $\epsilon$ with high probability. This implies the distributional policy evaluation problem can be solved with sample efficiency. Also, we show that under different mild assumptions a dataset of size $\widetilde O\left(\frac{|\mathcal{S}||\mathcal{A}|}{\epsilon^{2}(1-\gamma)^{4}}\right)$ suffices to ensure the Kolmogorov metric and total variation metric between $\hat\eta^\pi$ and $\eta^\pi$ is below $\epsilon$ with high probability. Furthermore, we investigate the asymptotic behavior of $\hat\eta^\pi$. We demonstrate that the ``empirical process'' $\sqrt{n}(\hat\eta^\pi-\eta^\pi)$ converges weakly to a Gaussian process in the space of bounded functionals on Lipschitz function class $\ell^\infty(\mathcal{F}_{W_1})$, also in the space of bounded functionals on indicator function class $\ell^\infty(\mathcal{F}_{\mathrm{KS}})$ and bounded measurable function class $\ell^\infty(\mathcal{F}_{\mathrm{TV}})$ when some mild conditions hold. Our findings give rise to a unified approach to statistical inference of a wide class of statistical functionals of $\eta^\pi$.

Asymptotic Behaviors and Phase Transitions in Projected Stochastic Approximation: A Jump Diffusion Approach

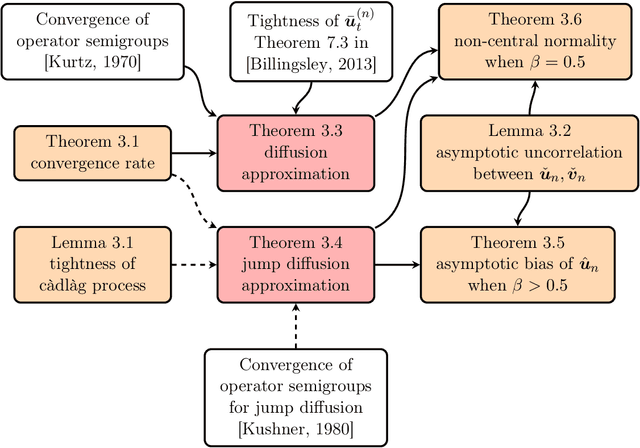
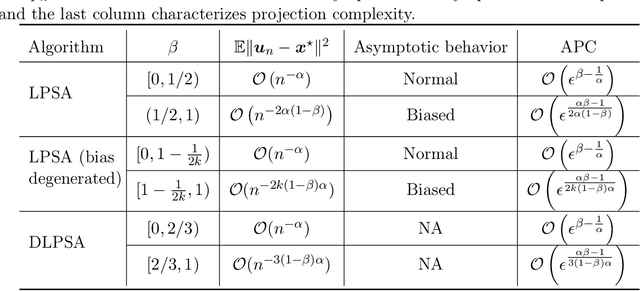
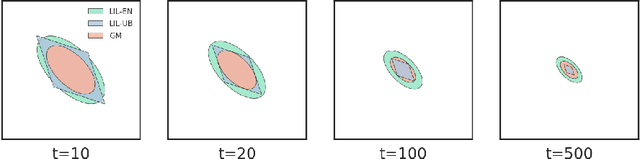
In this paper we consider linearly constrained optimization problems and propose a loopless projection stochastic approximation (LPSA) algorithm. It performs the projection with probability $p_n$ at the $n$-th iteration to ensure feasibility. Considering a specific family of the probability $p_n$ and step size $\eta_n$, we analyze our algorithm from an asymptotic and continuous perspective. Using a novel jump diffusion approximation, we show that the trajectories connecting those properly rescaled last iterates weakly converge to the solution of specific stochastic differential equations (SDEs). By analyzing SDEs, we identify the asymptotic behaviors of LPSA for different choices of $(p_n, \eta_n)$. We find that the algorithm presents an intriguing asymptotic bias-variance trade-off and yields phase transition phenomenons, according to the relative magnitude of $p_n$ w.r.t. $\eta_n$. This finding provides insights on selecting appropriate ${(p_n, \eta_n)}_{n \geq 1}$ to minimize the projection cost. Additionally, we propose the Debiased LPSA (DLPSA) as a practical application of our jump diffusion approximation result. DLPSA is shown to effectively reduce projection complexity compared to vanilla LPSA.

Online Statistical Inference for Nonlinear Stochastic Approximation with Markovian Data

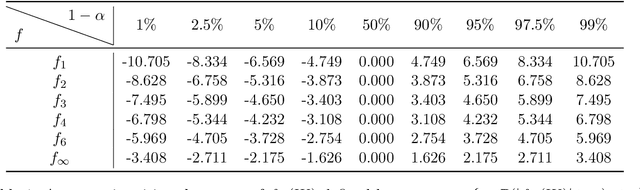
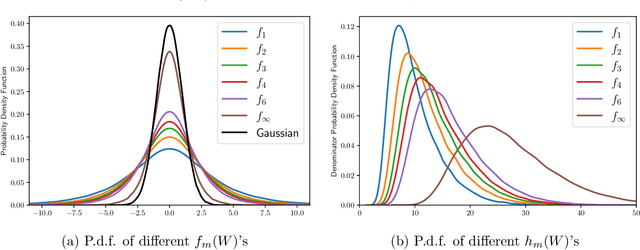
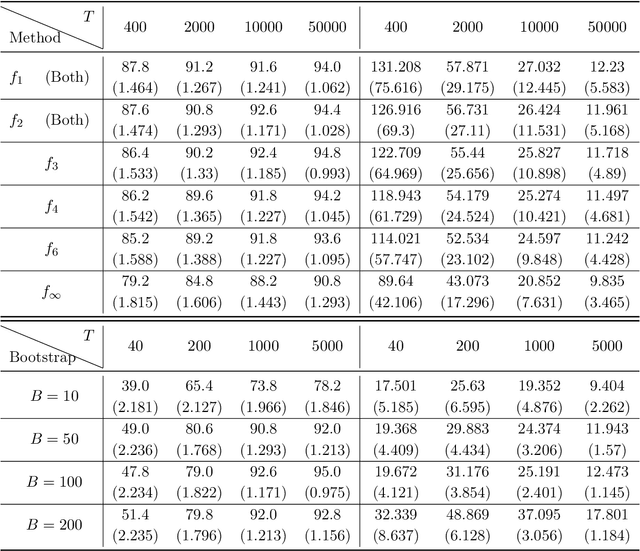
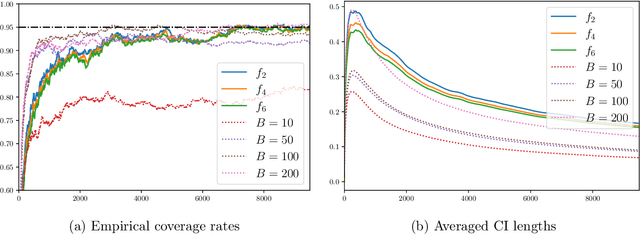
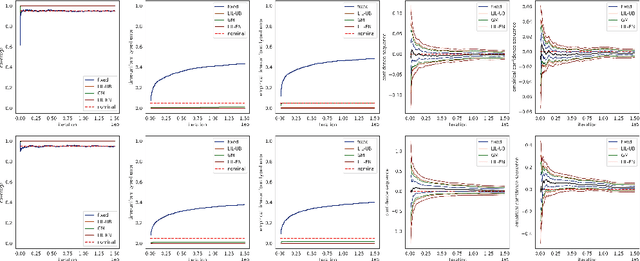
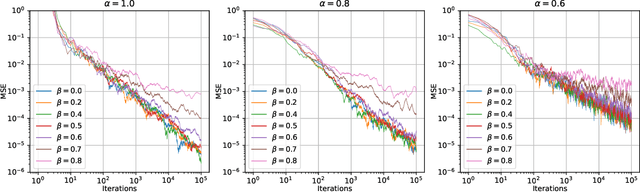
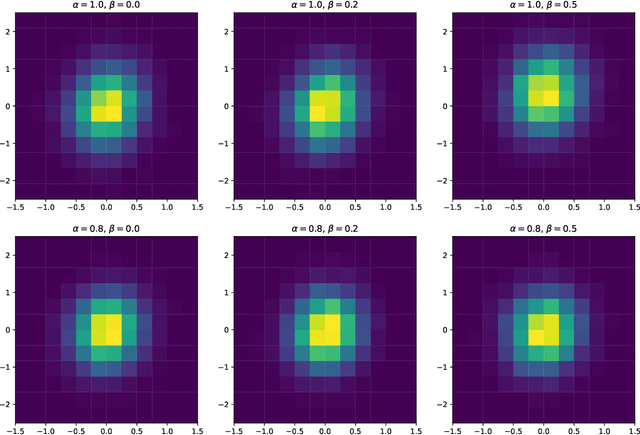
We study the statistical inference of nonlinear stochastic approximation algorithms utilizing a single trajectory of Markovian data. Our methodology has practical applications in various scenarios, such as Stochastic Gradient Descent (SGD) on autoregressive data and asynchronous Q-Learning. By utilizing the standard stochastic approximation (SA) framework to estimate the target parameter, we establish a functional central limit theorem for its partial-sum process, $\boldsymbol{\phi}_T$. To further support this theory, we provide a matching semiparametric efficient lower bound and a non-asymptotic upper bound on its weak convergence, measured in the L\'evy-Prokhorov metric. This functional central limit theorem forms the basis for our inference method. By selecting any continuous scale-invariant functional $f$, the asymptotic pivotal statistic $f(\boldsymbol{\phi}_T)$ becomes accessible, allowing us to construct an asymptotically valid confidence interval. We analyze the rejection probability of a family of functionals $f_m$, indexed by $m \in \mathbb{N}$, through theoretical and numerical means. The simulation results demonstrate the validity and efficiency of our method.

Layout-Bridging Text-to-Image Synthesis

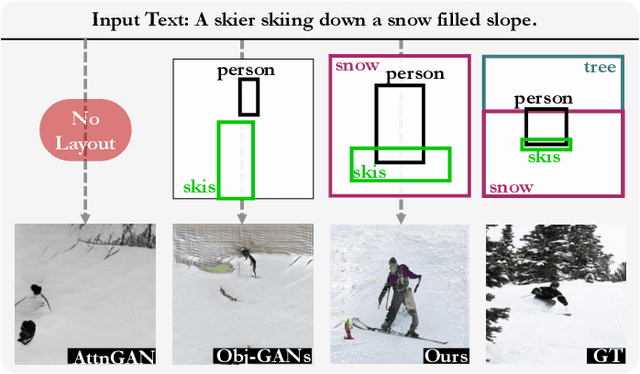
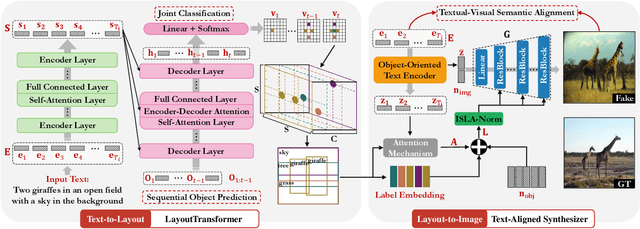
The crux of text-to-image synthesis stems from the difficulty of preserving the cross-modality semantic consistency between the input text and the synthesized image. Typical methods, which seek to model the text-to-image mapping directly, could only capture keywords in the text that indicates common objects or actions but fail to learn their spatial distribution patterns. An effective way to circumvent this limitation is to generate an image layout as guidance, which is attempted by a few methods. Nevertheless, these methods fail to generate practically effective layouts due to the diversity of input text and object location. In this paper we push for effective modeling in both text-to-layout generation and layout-to-image synthesis. Specifically, we formulate the text-to-layout generation as a sequence-to-sequence modeling task, and build our model upon Transformer to learn the spatial relationships between objects by modeling the sequential dependencies between them. In the stage of layout-to-image synthesis, we focus on learning the textual-visual semantic alignment per object in the layout to precisely incorporate the input text into the layout-to-image synthesizing process. To evaluate the quality of generated layout, we design a new metric specifically, dubbed Layout Quality Score, which considers both the absolute distribution errors of bounding boxes in the layout and the mutual spatial relationships between them. Extensive experiments on three datasets demonstrate the superior performance of our method over state-of-the-art methods on both predicting the layout and synthesizing the image from the given text.

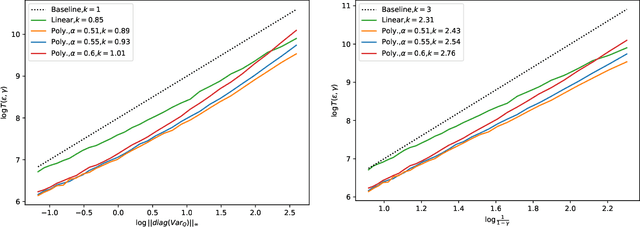
Polyak-Ruppert Averaged Q-Leaning is Statistically Efficient

We study synchronous Q-learning with Polyak-Ruppert averaging (a.k.a., averaged Q-learning) in a $\gamma$-discounted MDP. We establish a functional central limit theorem (FCLT) for the averaged iteration $\bar{\boldsymbol{Q}}_T$ and show its standardized partial-sum process weakly converges to a rescaled Brownian motion. Furthermore, we show that $\bar{\boldsymbol{Q}}_T$ is actually a regular asymptotically linear (RAL) estimator for the optimal Q-value function $\boldsymbol{Q}^*$ with the most efficient influence function. This implies the averaged Q-learning iteration has the smallest asymptotic variance among all RAL estimators. In addition, we present a non-asymptotic analysis for the $\ell_{\infty}$ error $\mathbb{E}\|\bar{\boldsymbol{Q}}_T-\boldsymbol{Q}^*\|_{\infty}$, showing for polynomial step sizes it matches the instance-dependent lower bound as well as the optimal minimax complexity lower bound. In short, our theoretical analysis shows averaged Q-learning is statistically efficient.

Statistical Estimation and Inference via Local SGD in Federated Learning

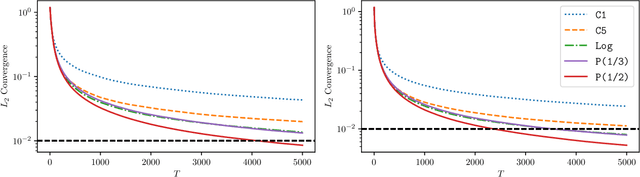
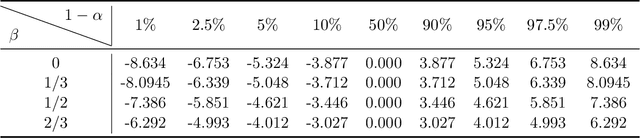
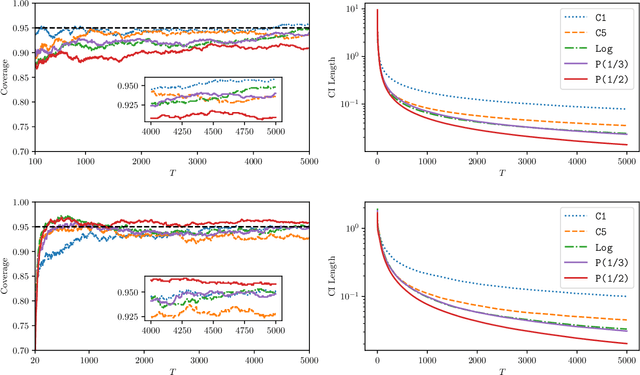
Federated Learning (FL) makes a large amount of edge computing devices (e.g., mobile phones) jointly learn a global model without data sharing. In FL, data are generated in a decentralized manner with high heterogeneity. This paper studies how to perform statistical estimation and inference in the federated setting. We analyze the so-called Local SGD, a multi-round estimation procedure that uses intermittent communication to improve communication efficiency. We first establish a {\it functional central limit theorem} that shows the averaged iterates of Local SGD weakly converge to a rescaled Brownian motion. We next provide two iterative inference methods: the {\it plug-in} and the {\it random scaling}. Random scaling constructs an asymptotically pivotal statistic for inference by using the information along the whole Local SGD path. Both the methods are communication efficient and applicable to online data. Our theoretical and empirical results show that Local SGD simultaneously achieves both statistical efficiency and communication efficiency.

Intervention Generative Adversarial Networks

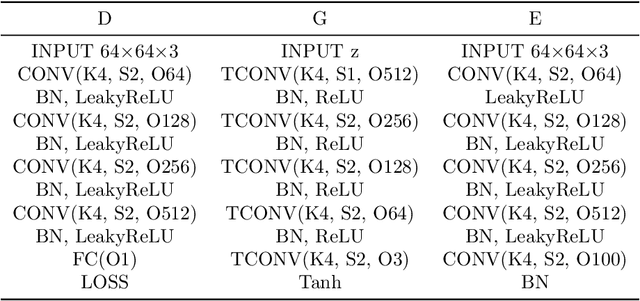
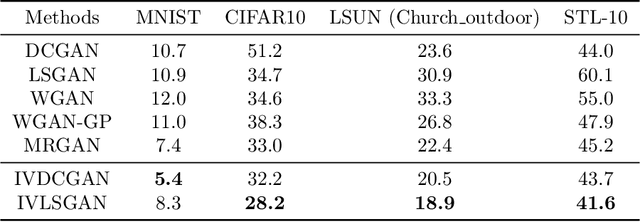
In this paper we propose a novel approach for stabilizing the training process of Generative Adversarial Networks as well as alleviating the mode collapse problem. The main idea is to introduce a regularization term that we call intervention loss into the objective. We refer to the resulting generative model as Intervention Generative Adversarial Networks (IVGAN). By perturbing the latent representations of real images obtained from an auxiliary encoder network with Gaussian invariant interventions and penalizing the dissimilarity of the distributions of the resulting generated images, the intervention loss provides more informative gradient for the generator, significantly improving GAN's training stability. We demonstrate the effectiveness and efficiency of our methods via solid theoretical analysis and thorough evaluation on standard real-world datasets as well as the stacked MNIST dataset.

CPGAN: Full-Spectrum Content-Parsing Generative Adversarial Networks for Text-to-Image Synthesis

Typical methods for text-to-image synthesis seek to design effective generative architecture to model the text-to-image mapping directly. It is fairly arduous due to the cross-modality translation involved in the task of text-to-image synthesis. In this paper we circumvent this problem by focusing on parsing the content of both the input text and the synthesized image thoroughly to model the text-to-image consistency in the semantic level. In particular, we design a memory structure to parse the textual content by exploring semantic correspondence between each word in the vocabulary to its various visual contexts across relevant images in training data during text encoding. On the other hand, the synthesized image is parsed to learn its semantics in an object-aware manner. Moreover, we customize a conditional discriminator, which models the fine-grained correlations between words and image sub-regions to push for the cross-modality semantic alignment between the input text and the synthesized image. Thus, a full-spectrum content-oriented parsing in the deep semantic level is performed by our model, which is referred to as Content-Parsing Generative Adversarial Networks (CPGAN). Extensive experiments on COCO dataset manifest that CPGAN advances the state-of-the-art performance significantly.