AKG kernel Agent: A Multi-Agent Framework for Cross-Platform Kernel Synthesis

Modern AI models demand high-performance computation kernels. The growing complexity of LLMs, multimodal architectures, and recommendation systems, combined with techniques like sparsity and quantization, creates significant computational challenges. Moreover, frequent hardware updates and diverse chip architectures further complicate this landscape, requiring tailored kernel implementations for each platform. However, manual optimization cannot keep pace with these demands, creating a critical bottleneck in AI system development. Recent advances in LLM code generation capabilities have opened new possibilities for automating kernel development. In this work, we propose AKG kernel agent (AI-driven Kernel Generator), a multi-agent system that automates kernel generation, migration, and performance tuning. AKG kernel agent is designed to support multiple domain-specific languages (DSLs), including Triton, TileLang, CPP, and CUDA-C, enabling it to target different hardware backends while maintaining correctness and portability. The system's modular design allows rapid integration of new DSLs and hardware targets. When evaluated on KernelBench using Triton DSL across GPU and NPU backends, AKG kernel agent achieves an average speedup of 1.46$\times$ over PyTorch Eager baselines implementations, demonstrating its effectiveness in accelerating kernel development for modern AI workloads.

Beyond Uniform Deletion: A Data Value-Weighted Framework for Certified Machine Unlearning

As the right to be forgotten becomes legislated worldwide, machine unlearning mechanisms have emerged to efficiently update models for data deletion and enhance user privacy protection. However, existing machine unlearning algorithms frequently neglect the fact that different data points may contribute unequally to model performance (i.e., heterogeneous data values). Treat them equally in machine unlearning procedure can potentially degrading the performance of updated models. To address this limitation, we propose Data Value-Weighted Unlearning (DVWU), a general unlearning framework that accounts for data value heterogeneity into the unlearning process. Specifically, we design a weighting strategy based on data values, which are then integrated into the unlearning procedure to enable differentiated unlearning for data points with varying utility to the model. The DVWU framework can be broadly adapted to various existing machine unlearning methods. We use the one-step Newton update as an example for implementation, developing both output and objective perturbation algorithms to achieve certified unlearning. Experiments on both synthetic and real-world datasets demonstrate that our methods achieve superior predictive performance and robustness compared to conventional unlearning approaches. We further show the extensibility of our framework on gradient ascent method by incorporating the proposed weighting strategy into the gradient terms, highlighting the adaptability of DVWU for broader gradient-based deep unlearning methods.

When and How Unlabeled Data Provably Improve In-Context Learning

Recent research shows that in-context learning (ICL) can be effective even when demonstrations have missing or incorrect labels. To shed light on this capability, we examine a canonical setting where the demonstrations are drawn according to a binary Gaussian mixture model (GMM) and a certain fraction of the demonstrations have missing labels. We provide a comprehensive theoretical study to show that: (1) The loss landscape of one-layer linear attention models recover the optimal fully-supervised estimator but completely fail to exploit unlabeled data; (2) In contrast, multilayer or looped transformers can effectively leverage unlabeled data by implicitly constructing estimators of the form $\sum_{i\ge 0} a_i (X^\top X)^iX^\top y$ with $X$ and $y$ denoting features and partially-observed labels (with missing entries set to zero). We characterize the class of polynomials that can be expressed as a function of depth and draw connections to Expectation Maximization, an iterative pseudo-labeling algorithm commonly used in semi-supervised learning. Importantly, the leading polynomial power is exponential in depth, so mild amount of depth/looping suffices. As an application of theory, we propose looping off-the-shelf tabular foundation models to enhance their semi-supervision capabilities. Extensive evaluations on real-world datasets show that our method significantly improves the semisupervised tabular learning performance over the standard single pass inference.

Continuum-armed Bandit Optimization with Batch Pairwise Comparison Oracles

This paper studies a bandit optimization problem where the goal is to maximize a function $f(x)$ over $T$ periods for some unknown strongly concave function $f$. We consider a new pairwise comparison oracle, where the decision-maker chooses a pair of actions $(x, x')$ for a consecutive number of periods and then obtains an estimate of $f(x)-f(x')$. We show that such a pairwise comparison oracle finds important applications to joint pricing and inventory replenishment problems and network revenue management. The challenge in this bandit optimization is twofold. First, the decision-maker not only needs to determine a pair of actions $(x, x')$ but also a stopping time $n$ (i.e., the number of queries based on $(x, x')$). Second, motivated by our inventory application, the estimate of the difference $f(x)-f(x')$ is biased, which is different from existing oracles in stochastic optimization literature. To address these challenges, we first introduce a discretization technique and local polynomial approximation to relate this problem to linear bandits. Then we developed a tournament successive elimination technique to localize the discretized cell and run an interactive batched version of LinUCB algorithm on cells. We establish regret bounds that are optimal up to poly-logarithmic factors. Furthermore, we apply our proposed algorithm and analytical framework to the two operations management problems and obtain results that improve state-of-the-art results in the existing literature.

Bayes-Optimal Fair Classification with Multiple Sensitive Features

Existing theoretical work on Bayes-optimal fair classifiers usually considers a single (binary) sensitive feature. In practice, individuals are often defined by multiple sensitive features. In this paper, we characterize the Bayes-optimal fair classifier for multiple sensitive features under general approximate fairness measures, including mean difference and mean ratio. We show that these approximate measures for existing group fairness notions, including Demographic Parity, Equal Opportunity, Predictive Equality, and Accuracy Parity, are linear transformations of selection rates for specific groups defined by both labels and sensitive features. We then characterize that Bayes-optimal fair classifiers for multiple sensitive features become instance-dependent thresholding rules that rely on a weighted sum of these group membership probabilities. Our framework applies to both attribute-aware and attribute-blind settings and can accommodate composite fairness notions like Equalized Odds. Building on this, we propose two practical algorithms for Bayes-optimal fair classification via in-processing and post-processing. We show empirically that our methods compare favorably to existing methods.

Provable Benefits of Task-Specific Prompts for In-context Learning

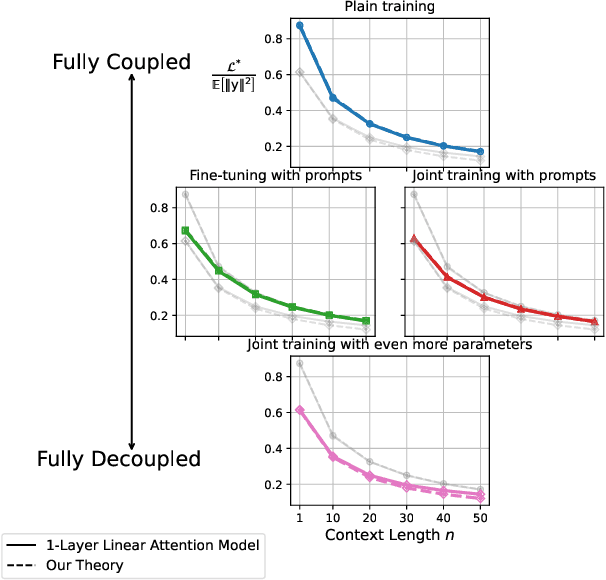
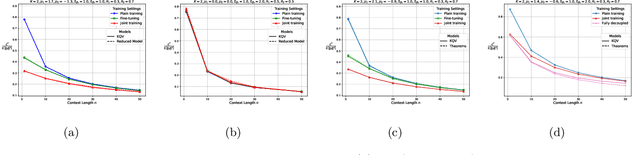
The in-context learning capabilities of modern language models have motivated a deeper mathematical understanding of sequence models. A line of recent work has shown that linear attention models can emulate projected gradient descent iterations to implicitly learn the task vector from the data provided in the context window. In this work, we consider a novel setting where the global task distribution can be partitioned into a union of conditional task distributions. We then examine the use of task-specific prompts and prediction heads for learning the prior information associated with the conditional task distribution using a one-layer attention model. Our results on loss landscape show that task-specific prompts facilitate a covariance-mean decoupling where prompt-tuning explains the conditional mean of the distribution whereas the variance is learned/explained through in-context learning. Incorporating task-specific head further aids this process by entirely decoupling estimation of mean and variance components. This covariance-mean perspective similarly explains how jointly training prompt and attention weights can provably help over fine-tuning after pretraining.

An Enhanced Zeroth-Order Stochastic Frank-Wolfe Framework for Constrained Finite-Sum Optimization

We propose an enhanced zeroth-order stochastic Frank-Wolfe framework to address constrained finite-sum optimization problems, a structure prevalent in large-scale machine-learning applications. Our method introduces a novel double variance reduction framework that effectively reduces the gradient approximation variance induced by zeroth-order oracles and the stochastic sampling variance from finite-sum objectives. By leveraging this framework, our algorithm achieves significant improvements in query efficiency, making it particularly well-suited for high-dimensional optimization tasks. Specifically, for convex objectives, the algorithm achieves a query complexity of O(d \sqrt{n}/\epsilon ) to find an epsilon-suboptimal solution, where d is the dimensionality and n is the number of functions in the finite-sum objective. For non-convex objectives, it achieves a query complexity of O(d^{3/2}\sqrt{n}/\epsilon^2 ) without requiring the computation ofd partial derivatives at each iteration. These complexities are the best known among zeroth-order stochastic Frank-Wolfe algorithms that avoid explicit gradient calculations. Empirical experiments on convex and non-convex machine learning tasks, including sparse logistic regression, robust classification, and adversarial attacks on deep networks, validate the computational efficiency and scalability of our approach. Our algorithm demonstrates superior performance in both convergence rate and query complexity compared to existing methods.

Selective Attention: Enhancing Transformer through Principled Context Control

The attention mechanism within the transformer architecture enables the model to weigh and combine tokens based on their relevance to the query. While self-attention has enjoyed major success, it notably treats all queries $q$ in the same way by applying the mapping $V^\top\text{softmax}(Kq)$, where $V,K$ are the value and key embeddings respectively. In this work, we argue that this uniform treatment hinders the ability to control contextual sparsity and relevance. As a solution, we introduce the $\textit{Selective Self-Attention}$ (SSA) layer that augments the softmax nonlinearity with a principled temperature scaling strategy. By controlling temperature, SSA adapts the contextual sparsity of the attention map to the query embedding and its position in the context window. Through theory and experiments, we demonstrate that this alleviates attention dilution, aids the optimization process, and enhances the model's ability to control softmax spikiness of individual queries. We also incorporate temperature scaling for value embeddings and show that it boosts the model's ability to suppress irrelevant/noisy tokens. Notably, SSA is a lightweight method which introduces less than 0.5% new parameters through a weight-sharing strategy and can be fine-tuned on existing LLMs. Extensive empirical evaluations demonstrate that SSA-equipped models achieve a noticeable and consistent accuracy improvement on language modeling benchmarks.

Towards Data Valuation via Asymmetric Data Shapley

As data emerges as a vital driver of technological and economic advancements, a key challenge is accurately quantifying its value in algorithmic decision-making. The Shapley value, a well-established concept from cooperative game theory, has been widely adopted to assess the contribution of individual data sources in supervised machine learning. However, its symmetry axiom assumes all players in the cooperative game are homogeneous, which overlooks the complex structures and dependencies present in real-world datasets. To address this limitation, we extend the traditional data Shapley framework to asymmetric data Shapley, making it flexible enough to incorporate inherent structures within the datasets for structure-aware data valuation. We also introduce an efficient $k$-nearest neighbor-based algorithm for its exact computation. We demonstrate the practical applicability of our framework across various machine learning tasks and data market contexts. The code is available at: https://github.com/xzheng01/Asymmetric-Data-Shapley.

Uncertainty Quantification of Data Shapley via Statistical Inference

As data plays an increasingly pivotal role in decision-making, the emergence of data markets underscores the growing importance of data valuation. Within the machine learning landscape, Data Shapley stands out as a widely embraced method for data valuation. However, a limitation of Data Shapley is its assumption of a fixed dataset, contrasting with the dynamic nature of real-world applications where data constantly evolves and expands. This paper establishes the relationship between Data Shapley and infinite-order U-statistics and addresses this limitation by quantifying the uncertainty of Data Shapley with changes in data distribution from the perspective of U-statistics. We make statistical inferences on data valuation to obtain confidence intervals for the estimations. We construct two different algorithms to estimate this uncertainty and provide recommendations for their applicable situations. We also conduct a series of experiments on various datasets to verify asymptotic normality and propose a practical trading scenario enabled by this method.