Yingcong Li
When and How Unlabeled Data Provably Improve In-Context Learning
Jun 18, 2025Abstract:Recent research shows that in-context learning (ICL) can be effective even when demonstrations have missing or incorrect labels. To shed light on this capability, we examine a canonical setting where the demonstrations are drawn according to a binary Gaussian mixture model (GMM) and a certain fraction of the demonstrations have missing labels. We provide a comprehensive theoretical study to show that: (1) The loss landscape of one-layer linear attention models recover the optimal fully-supervised estimator but completely fail to exploit unlabeled data; (2) In contrast, multilayer or looped transformers can effectively leverage unlabeled data by implicitly constructing estimators of the form $\sum_{i\ge 0} a_i (X^\top X)^iX^\top y$ with $X$ and $y$ denoting features and partially-observed labels (with missing entries set to zero). We characterize the class of polynomials that can be expressed as a function of depth and draw connections to Expectation Maximization, an iterative pseudo-labeling algorithm commonly used in semi-supervised learning. Importantly, the leading polynomial power is exponential in depth, so mild amount of depth/looping suffices. As an application of theory, we propose looping off-the-shelf tabular foundation models to enhance their semi-supervision capabilities. Extensive evaluations on real-world datasets show that our method significantly improves the semisupervised tabular learning performance over the standard single pass inference.
Gating is Weighting: Understanding Gated Linear Attention through In-context Learning
Apr 06, 2025Abstract:Linear attention methods offer a compelling alternative to softmax attention due to their efficiency in recurrent decoding. Recent research has focused on enhancing standard linear attention by incorporating gating while retaining its computational benefits. Such Gated Linear Attention (GLA) architectures include competitive models such as Mamba and RWKV. In this work, we investigate the in-context learning capabilities of the GLA model and make the following contributions. We show that a multilayer GLA can implement a general class of Weighted Preconditioned Gradient Descent (WPGD) algorithms with data-dependent weights. These weights are induced by the gating mechanism and the input, enabling the model to control the contribution of individual tokens to prediction. To further understand the mechanics of this weighting, we introduce a novel data model with multitask prompts and characterize the optimization landscape of learning a WPGD algorithm. Under mild conditions, we establish the existence and uniqueness (up to scaling) of a global minimum, corresponding to a unique WPGD solution. Finally, we translate these findings to explore the optimization landscape of GLA and shed light on how gating facilitates context-aware learning and when it is provably better than vanilla linear attention.
Provable Benefits of Task-Specific Prompts for In-context Learning
Mar 05, 2025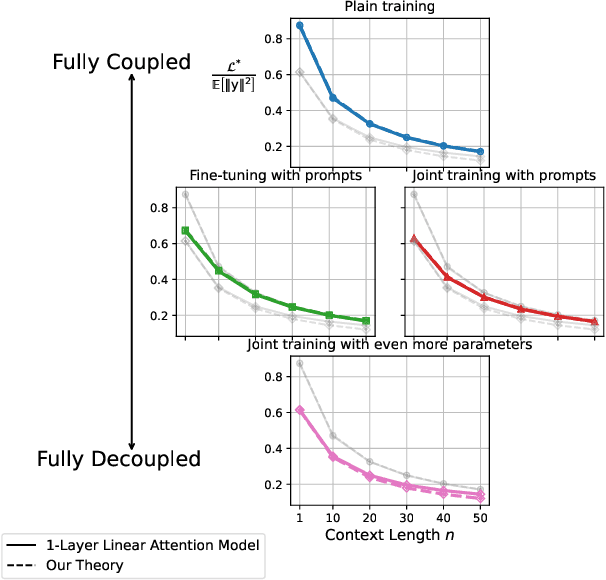
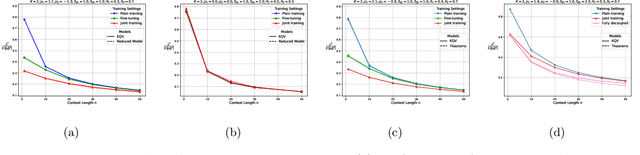
Abstract:The in-context learning capabilities of modern language models have motivated a deeper mathematical understanding of sequence models. A line of recent work has shown that linear attention models can emulate projected gradient descent iterations to implicitly learn the task vector from the data provided in the context window. In this work, we consider a novel setting where the global task distribution can be partitioned into a union of conditional task distributions. We then examine the use of task-specific prompts and prediction heads for learning the prior information associated with the conditional task distribution using a one-layer attention model. Our results on loss landscape show that task-specific prompts facilitate a covariance-mean decoupling where prompt-tuning explains the conditional mean of the distribution whereas the variance is learned/explained through in-context learning. Incorporating task-specific head further aids this process by entirely decoupling estimation of mean and variance components. This covariance-mean perspective similarly explains how jointly training prompt and attention weights can provably help over fine-tuning after pretraining.
Fine-grained Analysis of In-context Linear Estimation: Data, Architecture, and Beyond
Jul 13, 2024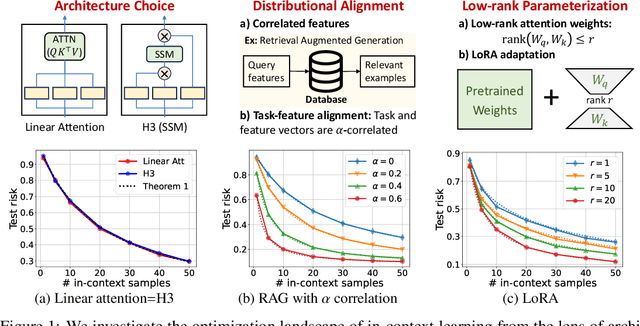
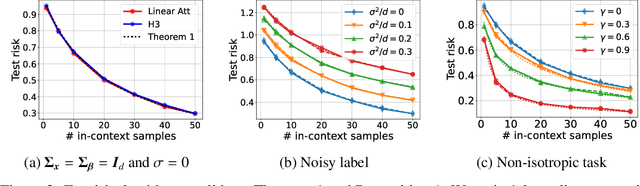
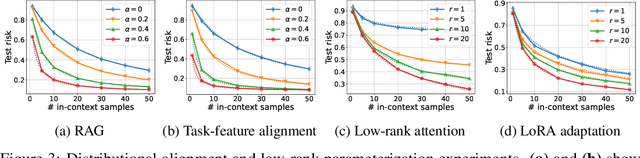
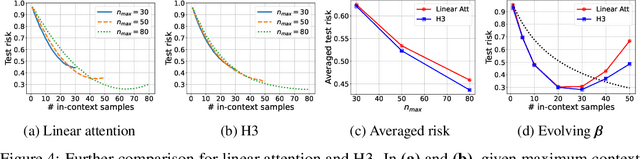
Abstract:Recent research has shown that Transformers with linear attention are capable of in-context learning (ICL) by implementing a linear estimator through gradient descent steps. However, the existing results on the optimization landscape apply under stylized settings where task and feature vectors are assumed to be IID and the attention weights are fully parameterized. In this work, we develop a stronger characterization of the optimization and generalization landscape of ICL through contributions on architectures, low-rank parameterization, and correlated designs: (1) We study the landscape of 1-layer linear attention and 1-layer H3, a state-space model. Under a suitable correlated design assumption, we prove that both implement 1-step preconditioned gradient descent. We show that thanks to its native convolution filters, H3 also has the advantage of implementing sample weighting and outperforming linear attention in suitable settings. (2) By studying correlated designs, we provide new risk bounds for retrieval augmented generation (RAG) and task-feature alignment which reveal how ICL sample complexity benefits from distributional alignment. (3) We derive the optimal risk for low-rank parameterized attention weights in terms of covariance spectrum. Through this, we also shed light on how LoRA can adapt to a new distribution by capturing the shift between task covariances. Experimental results corroborate our theoretical findings. Overall, this work explores the optimization and risk landscape of ICL in practically meaningful settings and contributes to a more thorough understanding of its mechanics.
Mechanics of Next Token Prediction with Self-Attention
Mar 12, 2024



Abstract:Transformer-based language models are trained on large datasets to predict the next token given an input sequence. Despite this simple training objective, they have led to revolutionary advances in natural language processing. Underlying this success is the self-attention mechanism. In this work, we ask: $\textit{What}$ $\textit{does}$ $\textit{a}$ $\textit{single}$ $\textit{self-attention}$ $\textit{layer}$ $\textit{learn}$ $\textit{from}$ $\textit{next-token}$ $\textit{prediction?}$ We show that training self-attention with gradient descent learns an automaton which generates the next token in two distinct steps: $\textbf{(1)}$ $\textbf{Hard}$ $\textbf{retrieval:}$ Given input sequence, self-attention precisely selects the $\textit{high-priority}$ $\textit{input}$ $\textit{tokens}$ associated with the last input token. $\textbf{(2)}$ $\textbf{Soft}$ $\textbf{composition:}$ It then creates a convex combination of the high-priority tokens from which the next token can be sampled. Under suitable conditions, we rigorously characterize these mechanics through a directed graph over tokens extracted from the training data. We prove that gradient descent implicitly discovers the strongly-connected components (SCC) of this graph and self-attention learns to retrieve the tokens that belong to the highest-priority SCC available in the context window. Our theory relies on decomposing the model weights into a directional component and a finite component that correspond to hard retrieval and soft composition steps respectively. This also formalizes a related implicit bias formula conjectured in [Tarzanagh et al. 2023]. We hope that these findings shed light on how self-attention processes sequential data and pave the path toward demystifying more complex architectures.
From Self-Attention to Markov Models: Unveiling the Dynamics of Generative Transformers
Feb 21, 2024



Abstract:Modern language models rely on the transformer architecture and attention mechanism to perform language understanding and text generation. In this work, we study learning a 1-layer self-attention model from a set of prompts and associated output data sampled from the model. We first establish a precise mapping between the self-attention mechanism and Markov models: Inputting a prompt to the model samples the output token according to a context-conditioned Markov chain (CCMC) which weights the transition matrix of a base Markov chain. Additionally, incorporating positional encoding results in position-dependent scaling of the transition probabilities. Building on this formalism, we develop identifiability/coverage conditions for the prompt distribution that guarantee consistent estimation and establish sample complexity guarantees under IID samples. Finally, we study the problem of learning from a single output trajectory generated from an initial prompt. We characterize an intriguing winner-takes-all phenomenon where the generative process implemented by self-attention collapses into sampling a limited subset of tokens due to its non-mixing nature. This provides a mathematical explanation to the tendency of modern LLMs to generate repetitive text. In summary, the equivalence to CCMC provides a simple but powerful framework to study self-attention and its properties.
Transformers as Support Vector Machines
Sep 07, 2023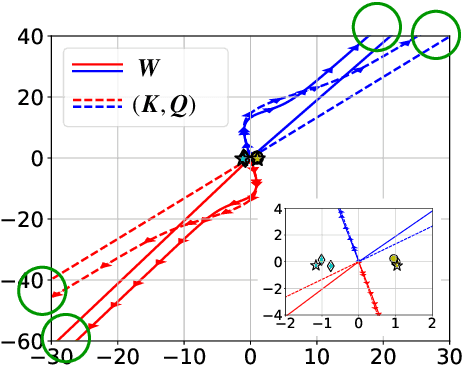
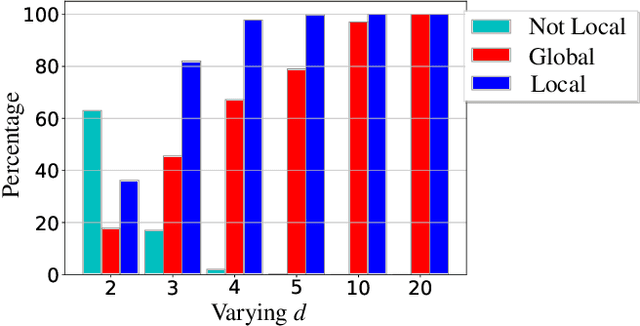
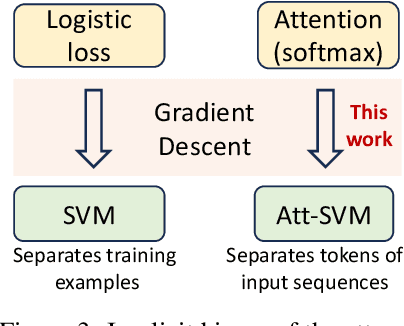
Abstract:Since its inception in "Attention Is All You Need", transformer architecture has led to revolutionary advancements in NLP. The attention layer within the transformer admits a sequence of input tokens $X$ and makes them interact through pairwise similarities computed as softmax$(XQK^\top X^\top)$, where $(K,Q)$ are the trainable key-query parameters. In this work, we establish a formal equivalence between the optimization geometry of self-attention and a hard-margin SVM problem that separates optimal input tokens from non-optimal tokens using linear constraints on the outer-products of token pairs. This formalism allows us to characterize the implicit bias of 1-layer transformers optimized with gradient descent: (1) Optimizing the attention layer with vanishing regularization, parameterized by $(K,Q)$, converges in direction to an SVM solution minimizing the nuclear norm of the combined parameter $W=KQ^\top$. Instead, directly parameterizing by $W$ minimizes a Frobenius norm objective. We characterize this convergence, highlighting that it can occur toward locally-optimal directions rather than global ones. (2) Complementing this, we prove the local/global directional convergence of gradient descent under suitable geometric conditions. Importantly, we show that over-parameterization catalyzes global convergence by ensuring the feasibility of the SVM problem and by guaranteeing a benign optimization landscape devoid of stationary points. (3) While our theory applies primarily to linear prediction heads, we propose a more general SVM equivalence that predicts the implicit bias with nonlinear heads. Our findings are applicable to arbitrary datasets and their validity is verified via experiments. We also introduce several open problems and research directions. We believe these findings inspire the interpretation of transformers as a hierarchy of SVMs that separates and selects optimal tokens.
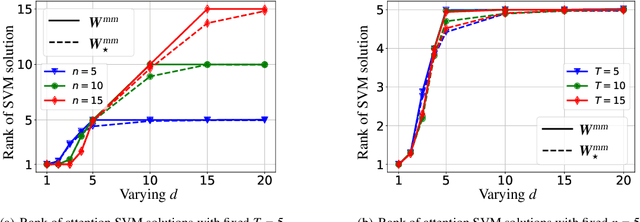
Max-Margin Token Selection in Attention Mechanism
Jun 27, 2023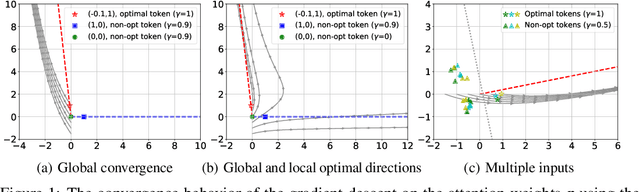
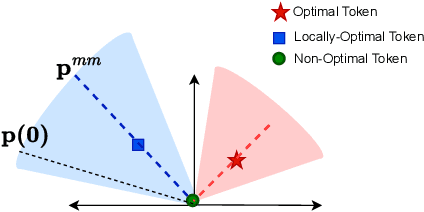
Abstract:Attention mechanism is a central component of the transformer architecture which led to the phenomenal success of large language models. However, the theoretical principles underlying the attention mechanism are poorly understood, especially its nonconvex optimization dynamics. In this work, we explore the seminal softmax-attention model $f(\boldsymbol{X})=\langle \boldsymbol{Xv}, \texttt{softmax}(\boldsymbol{XWp})\rangle$, where $\boldsymbol{X}$ is the token sequence and $(\boldsymbol{v},\boldsymbol{W},\boldsymbol{p})$ are trainable parameters. We prove that running gradient descent on $\boldsymbol{p}$, or equivalently $\boldsymbol{W}$, converges in direction to a max-margin solution that separates $\textit{locally-optimal}$ tokens from non-optimal ones. This clearly formalizes attention as an optimal token selection mechanism. Remarkably, our results are applicable to general data and precisely characterize $\textit{optimality}$ of tokens in terms of the value embeddings $\boldsymbol{Xv}$ and problem geometry. We also provide a broader regularization path analysis that establishes the margin maximizing nature of attention even for nonlinear prediction heads. When optimizing $\boldsymbol{v}$ and $\boldsymbol{p}$ simultaneously with logistic loss, we identify conditions under which the regularization paths directionally converge to their respective hard-margin SVM solutions where $\boldsymbol{v}$ separates the input features based on their labels. Interestingly, the SVM formulation of $\boldsymbol{p}$ is influenced by the support vector geometry of $\boldsymbol{v}$. Finally, we verify our theoretical findings via numerical experiments and provide insights.
Dissecting Chain-of-Thought: A Study on Compositional In-Context Learning of MLPs
May 30, 2023
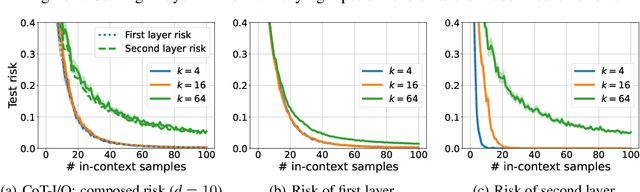
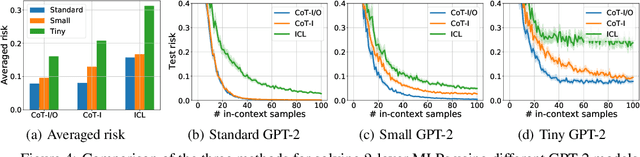
Abstract:Chain-of-thought (CoT) is a method that enables language models to handle complex reasoning tasks by decomposing them into simpler steps. Despite its success, the underlying mechanics of CoT are not yet fully understood. In an attempt to shed light on this, our study investigates the impact of CoT on the ability of transformers to in-context learn a simple to study, yet general family of compositional functions: multi-layer perceptrons (MLPs). In this setting, we reveal that the success of CoT can be attributed to breaking down in-context learning of a compositional function into two distinct phases: focusing on data related to each step of the composition and in-context learning the single-step composition function. Through both experimental and theoretical evidence, we demonstrate how CoT significantly reduces the sample complexity of in-context learning (ICL) and facilitates the learning of complex functions that non-CoT methods struggle with. Furthermore, we illustrate how transformers can transition from vanilla in-context learning to mastering a compositional function with CoT by simply incorporating an additional layer that performs the necessary filtering for CoT via the attention mechanism. In addition to these test-time benefits, we highlight how CoT accelerates pretraining by learning shortcuts to represent complex functions and how filtering plays an important role in pretraining. These findings collectively provide insights into the mechanics of CoT, inviting further investigation of its role in complex reasoning tasks.
Provable Pathways: Learning Multiple Tasks over Multiple Paths
Mar 08, 2023



Abstract:Constructing useful representations across a large number of tasks is a key requirement for sample-efficient intelligent systems. A traditional idea in multitask learning (MTL) is building a shared representation across tasks which can then be adapted to new tasks by tuning last layers. A desirable refinement of using a shared one-fits-all representation is to construct task-specific representations. To this end, recent PathNet/muNet architectures represent individual tasks as pathways within a larger supernet. The subnetworks induced by pathways can be viewed as task-specific representations that are composition of modules within supernet's computation graph. This work explores the pathways proposal from the lens of statistical learning: We first develop novel generalization bounds for empirical risk minimization problems learning multiple tasks over multiple paths (Multipath MTL). In conjunction, we formalize the benefits of resulting multipath representation when adapting to new downstream tasks. Our bounds are expressed in terms of Gaussian complexity, lead to tangible guarantees for the class of linear representations, and provide novel insights into the quality and benefits of a multipath representation. When computation graph is a tree, Multipath MTL hierarchically clusters the tasks and builds cluster-specific representations. We provide further discussion and experiments for hierarchical MTL and rigorously identify the conditions under which Multipath MTL is provably superior to traditional MTL approaches with shallow supernets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge