Davoud Ataee Tarzanagh
PaVeRL-SQL: Text-to-SQL via Partial-Match Rewards and Verbal Reinforcement Learning
Sep 08, 2025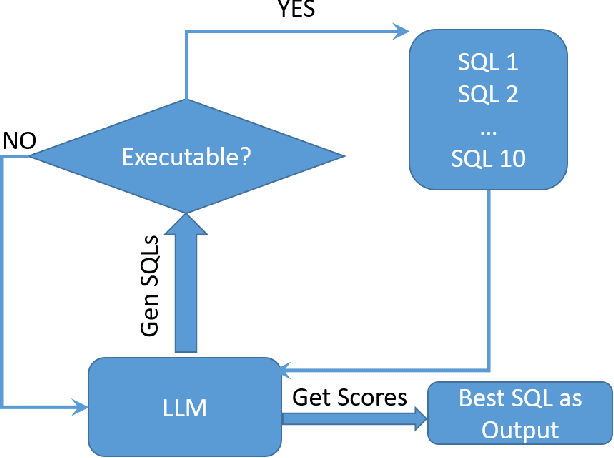
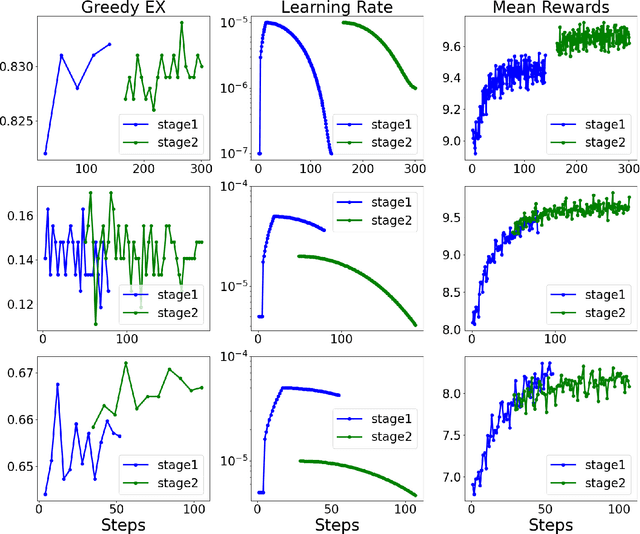
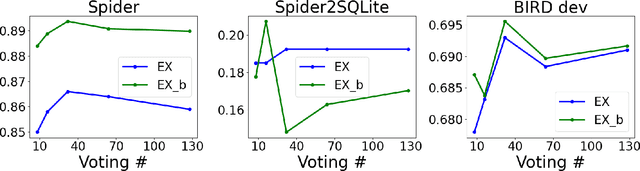
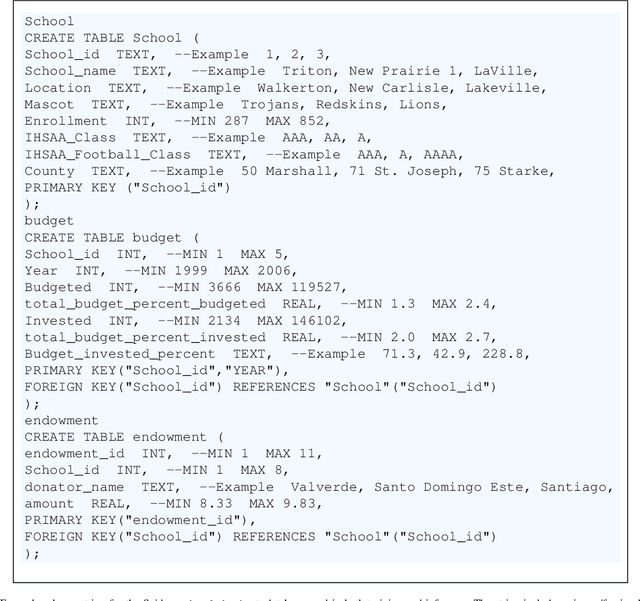
Abstract:Text-to-SQL models allow users to interact with a database more easily by generating executable SQL statements from natural-language questions. Despite recent successes on simpler databases and questions, current Text-to-SQL methods still suffer from low execution accuracy on industry-scale databases and complex questions involving domain-specific business logic. We present \emph{PaVeRL-SQL}, a framework that combines \emph{Partial-Match Rewards} and \emph{Verbal Reinforcement Learning} to drive self-improvement in reasoning language models (RLMs) for Text-to-SQL. To handle practical use cases, we adopt two pipelines: (1) a newly designed in-context learning framework with group self-evaluation (verbal-RL), using capable open- and closed-source large language models (LLMs) as backbones; and (2) a chain-of-thought (CoT) RL pipeline with a small backbone model (OmniSQL-7B) trained with a specially designed reward function and two-stage RL. These pipelines achieve state-of-the-art (SOTA) results on popular Text-to-SQL benchmarks -- Spider, Spider 2.0, and BIRD. For the industrial-level Spider2.0-SQLite benchmark, the verbal-RL pipeline achieves an execution accuracy 7.4\% higher than SOTA, and the CoT pipeline is 1.4\% higher. RL training with mixed SQL dialects yields strong, threefold gains, particularly for dialects with limited training data. Overall, \emph{PaVeRL-SQL} delivers reliable, SOTA Text-to-SQL under realistic industrial constraints. The code is available at https://github.com/PaVeRL-SQL/PaVeRL-SQL.
Truncated Matrix Completion - An Empirical Study
Apr 14, 2025Abstract:Low-rank Matrix Completion (LRMC) describes the problem where we wish to recover missing entries of partially observed low-rank matrix. Most existing matrix completion work deals with sampling procedures that are independent of the underlying data values. While this assumption allows the derivation of nice theoretical guarantees, it seldom holds in real-world applications. In this paper, we consider various settings where the sampling mask is dependent on the underlying data values, motivated by applications in sensing, sequential decision-making, and recommender systems. Through a series of experiments, we study and compare the performance of various LRMC algorithms that were originally successful for data-independent sampling patterns.
Gating is Weighting: Understanding Gated Linear Attention through In-context Learning
Apr 06, 2025Abstract:Linear attention methods offer a compelling alternative to softmax attention due to their efficiency in recurrent decoding. Recent research has focused on enhancing standard linear attention by incorporating gating while retaining its computational benefits. Such Gated Linear Attention (GLA) architectures include competitive models such as Mamba and RWKV. In this work, we investigate the in-context learning capabilities of the GLA model and make the following contributions. We show that a multilayer GLA can implement a general class of Weighted Preconditioned Gradient Descent (WPGD) algorithms with data-dependent weights. These weights are induced by the gating mechanism and the input, enabling the model to control the contribution of individual tokens to prediction. To further understand the mechanics of this weighting, we introduce a novel data model with multitask prompts and characterize the optimization landscape of learning a WPGD algorithm. Under mild conditions, we establish the existence and uniqueness (up to scaling) of a global minimum, corresponding to a unique WPGD solution. Finally, we translate these findings to explore the optimization landscape of GLA and shed light on how gating facilitates context-aware learning and when it is provably better than vanilla linear attention.
SEFD: Semantic-Enhanced Framework for Detecting LLM-Generated Text
Nov 17, 2024Abstract:The widespread adoption of large language models (LLMs) has created an urgent need for robust tools to detect LLM-generated text, especially in light of \textit{paraphrasing} techniques that often evade existing detection methods. To address this challenge, we present a novel semantic-enhanced framework for detecting LLM-generated text (SEFD) that leverages a retrieval-based mechanism to fully utilize text semantics. Our framework improves upon existing detection methods by systematically integrating retrieval-based techniques with traditional detectors, employing a carefully curated retrieval mechanism that strikes a balance between comprehensive coverage and computational efficiency. We showcase the effectiveness of our approach in sequential text scenarios common in real-world applications, such as online forums and Q\&A platforms. Through comprehensive experiments across various LLM-generated texts and detection methods, we demonstrate that our framework substantially enhances detection accuracy in paraphrasing scenarios while maintaining robustness for standard LLM-generated content.
Optimizing Attention with Mirror Descent: Generalized Max-Margin Token Selection
Oct 18, 2024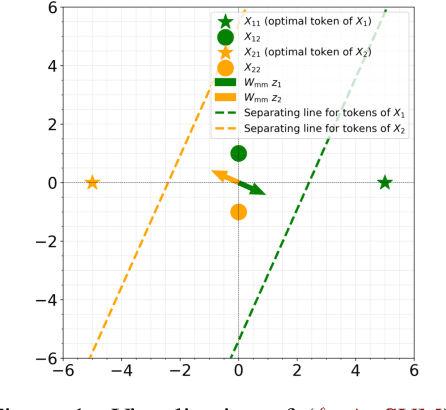
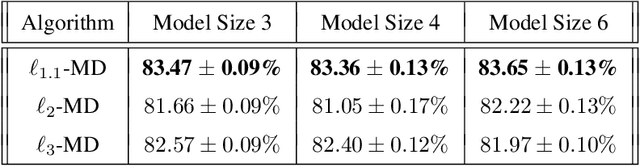
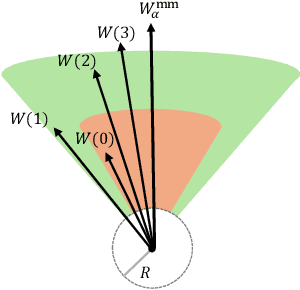
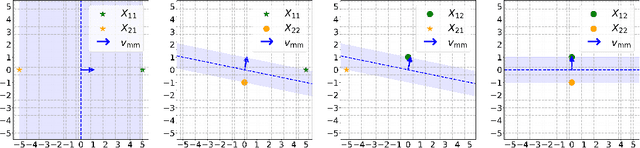
Abstract:Attention mechanisms have revolutionized several domains of artificial intelligence, such as natural language processing and computer vision, by enabling models to selectively focus on relevant parts of the input data. While recent work has characterized the optimization dynamics of gradient descent (GD) in attention-based models and the structural properties of its preferred solutions, less is known about more general optimization algorithms such as mirror descent (MD). In this paper, we investigate the convergence properties and implicit biases of a family of MD algorithms tailored for softmax attention mechanisms, with the potential function chosen as the $p$-th power of the $\ell_p$-norm. Specifically, we show that these algorithms converge in direction to a generalized hard-margin SVM with an $\ell_p$-norm objective when applied to a classification problem using a softmax attention model. Notably, our theoretical results reveal that the convergence rate is comparable to that of traditional GD in simpler models, despite the highly nonlinear and nonconvex nature of the present problem. Additionally, we delve into the joint optimization dynamics of the key-query matrix and the decoder, establishing conditions under which this complex joint optimization converges to their respective hard-margin SVM solutions. Lastly, our numerical experiments on real data demonstrate that MD algorithms improve generalization over standard GD and excel in optimal token selection.
Clustering Alzheimer's Disease Subtypes via Similarity Learning and Graph Diffusion
Oct 04, 2024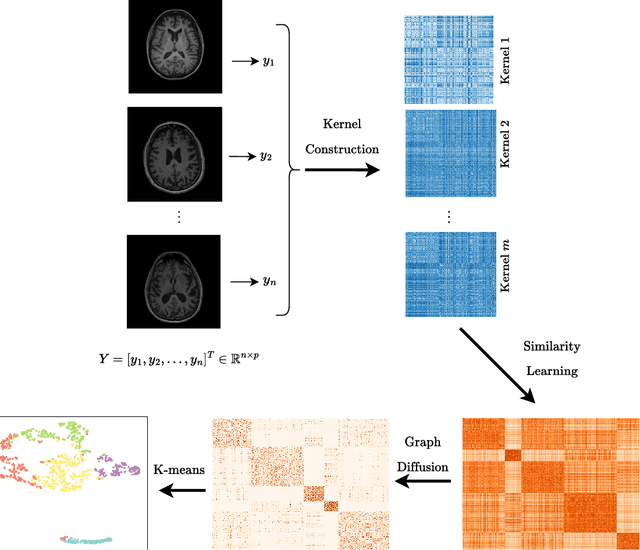
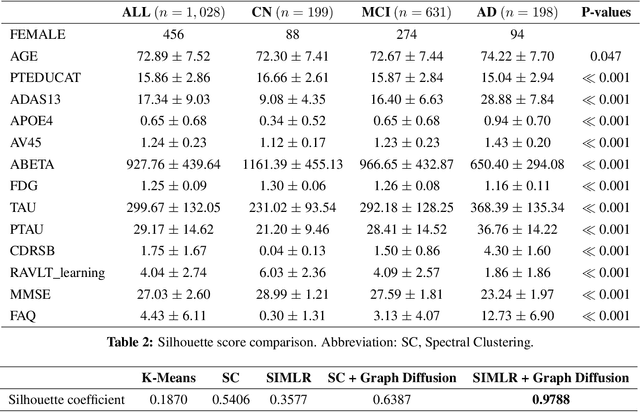
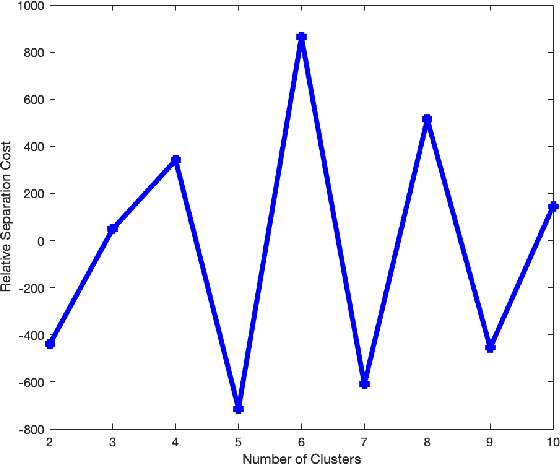
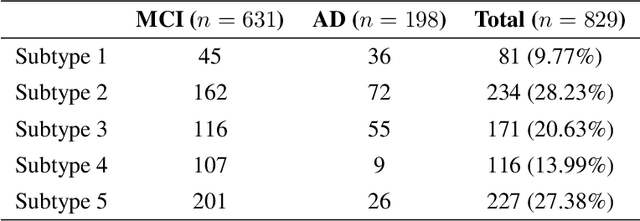
Abstract:Alzheimer's disease (AD) is a complex neurodegenerative disorder that affects millions of people worldwide. Due to the heterogeneous nature of AD, its diagnosis and treatment pose critical challenges. Consequently, there is a growing research interest in identifying homogeneous AD subtypes that can assist in addressing these challenges in recent years. In this study, we aim to identify subtypes of AD that represent distinctive clinical features and underlying pathology by utilizing unsupervised clustering with graph diffusion and similarity learning. We adopted SIMLR, a multi-kernel similarity learning framework, and graph diffusion to perform clustering on a group of 829 patients with AD and mild cognitive impairment (MCI, a prodromal stage of AD) based on their cortical thickness measurements extracted from magnetic resonance imaging (MRI) scans. Although the clustering approach we utilized has not been explored for the task of AD subtyping before, it demonstrated significantly better performance than several commonly used clustering methods. Specifically, we showed the power of graph diffusion in reducing the effects of noise in the subtype detection. Our results revealed five subtypes that differed remarkably in their biomarkers, cognitive status, and some other clinical features. To evaluate the resultant subtypes further, a genetic association study was carried out and successfully identified potential genetic underpinnings of different AD subtypes. Our source code is available at: https://github.com/PennShenLab/AD-SIMLR.
Fairness-Aware Estimation of Graphical Models
Aug 30, 2024Abstract:This paper examines the issue of fairness in the estimation of graphical models (GMs), particularly Gaussian, Covariance, and Ising models. These models play a vital role in understanding complex relationships in high-dimensional data. However, standard GMs can result in biased outcomes, especially when the underlying data involves sensitive characteristics or protected groups. To address this, we introduce a comprehensive framework designed to reduce bias in the estimation of GMs related to protected attributes. Our approach involves the integration of the pairwise graph disparity error and a tailored loss function into a nonsmooth multi-objective optimization problem, striving to achieve fairness across different sensitive groups while maintaining the effectiveness of the GMs. Experimental evaluations on synthetic and real-world datasets demonstrate that our framework effectively mitigates bias without undermining GMs' performance.
Fair Canonical Correlation Analysis
Sep 27, 2023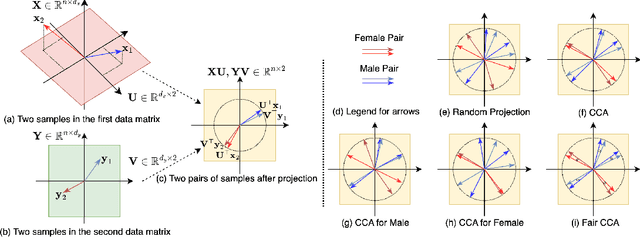
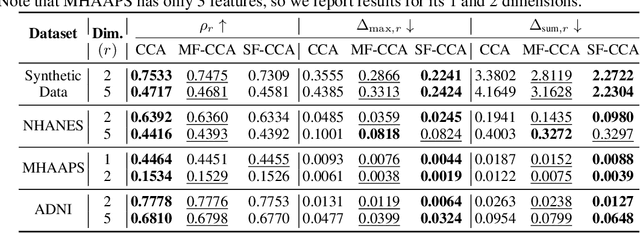
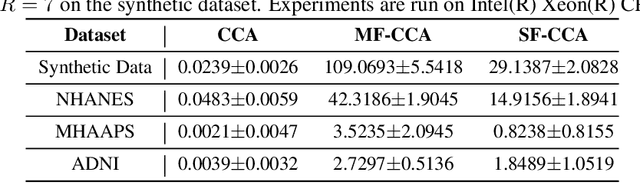
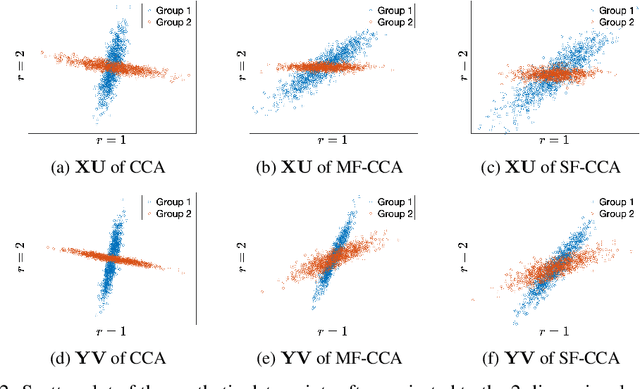
Abstract:This paper investigates fairness and bias in Canonical Correlation Analysis (CCA), a widely used statistical technique for examining the relationship between two sets of variables. We present a framework that alleviates unfairness by minimizing the correlation disparity error associated with protected attributes. Our approach enables CCA to learn global projection matrices from all data points while ensuring that these matrices yield comparable correlation levels to group-specific projection matrices. Experimental evaluation on both synthetic and real-world datasets demonstrates the efficacy of our method in reducing correlation disparity error without compromising CCA accuracy.
Transformers as Support Vector Machines
Sep 07, 2023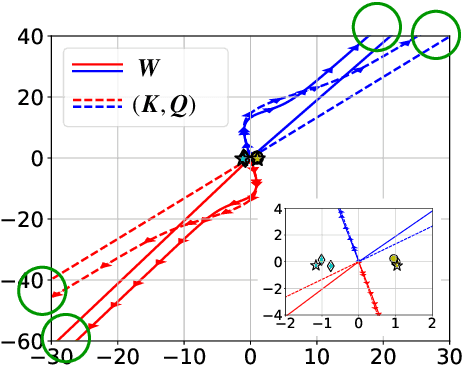
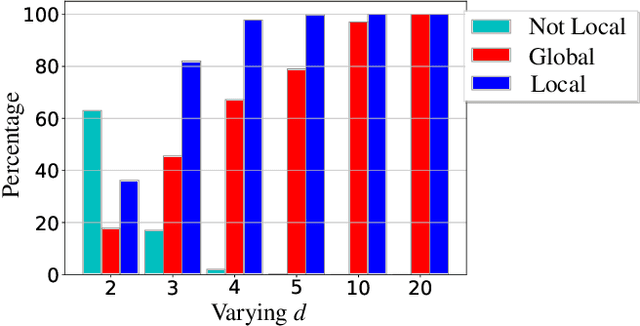
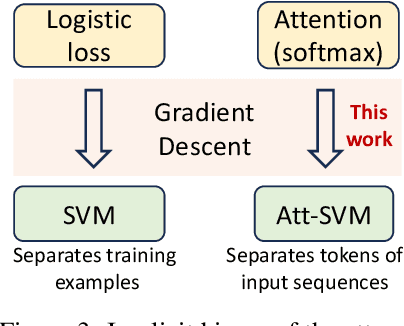
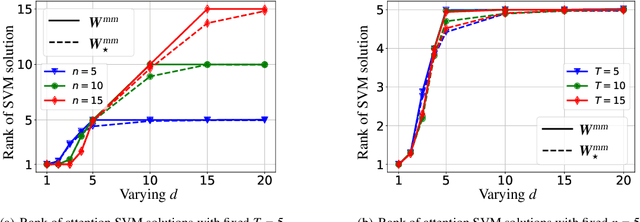
Abstract:Since its inception in "Attention Is All You Need", transformer architecture has led to revolutionary advancements in NLP. The attention layer within the transformer admits a sequence of input tokens $X$ and makes them interact through pairwise similarities computed as softmax$(XQK^\top X^\top)$, where $(K,Q)$ are the trainable key-query parameters. In this work, we establish a formal equivalence between the optimization geometry of self-attention and a hard-margin SVM problem that separates optimal input tokens from non-optimal tokens using linear constraints on the outer-products of token pairs. This formalism allows us to characterize the implicit bias of 1-layer transformers optimized with gradient descent: (1) Optimizing the attention layer with vanishing regularization, parameterized by $(K,Q)$, converges in direction to an SVM solution minimizing the nuclear norm of the combined parameter $W=KQ^\top$. Instead, directly parameterizing by $W$ minimizes a Frobenius norm objective. We characterize this convergence, highlighting that it can occur toward locally-optimal directions rather than global ones. (2) Complementing this, we prove the local/global directional convergence of gradient descent under suitable geometric conditions. Importantly, we show that over-parameterization catalyzes global convergence by ensuring the feasibility of the SVM problem and by guaranteeing a benign optimization landscape devoid of stationary points. (3) While our theory applies primarily to linear prediction heads, we propose a more general SVM equivalence that predicts the implicit bias with nonlinear heads. Our findings are applicable to arbitrary datasets and their validity is verified via experiments. We also introduce several open problems and research directions. We believe these findings inspire the interpretation of transformers as a hierarchy of SVMs that separates and selects optimal tokens.
Max-Margin Token Selection in Attention Mechanism
Jun 27, 2023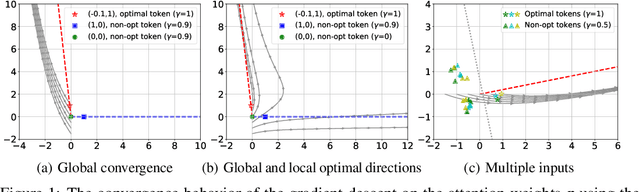
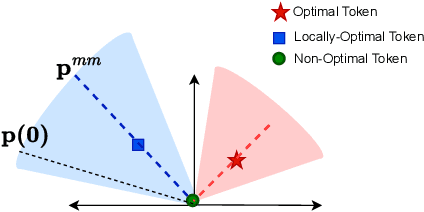
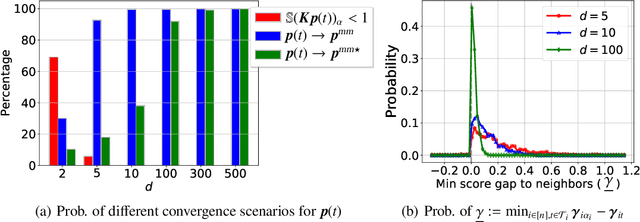
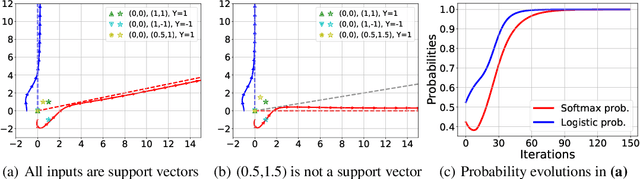
Abstract:Attention mechanism is a central component of the transformer architecture which led to the phenomenal success of large language models. However, the theoretical principles underlying the attention mechanism are poorly understood, especially its nonconvex optimization dynamics. In this work, we explore the seminal softmax-attention model $f(\boldsymbol{X})=\langle \boldsymbol{Xv}, \texttt{softmax}(\boldsymbol{XWp})\rangle$, where $\boldsymbol{X}$ is the token sequence and $(\boldsymbol{v},\boldsymbol{W},\boldsymbol{p})$ are trainable parameters. We prove that running gradient descent on $\boldsymbol{p}$, or equivalently $\boldsymbol{W}$, converges in direction to a max-margin solution that separates $\textit{locally-optimal}$ tokens from non-optimal ones. This clearly formalizes attention as an optimal token selection mechanism. Remarkably, our results are applicable to general data and precisely characterize $\textit{optimality}$ of tokens in terms of the value embeddings $\boldsymbol{Xv}$ and problem geometry. We also provide a broader regularization path analysis that establishes the margin maximizing nature of attention even for nonlinear prediction heads. When optimizing $\boldsymbol{v}$ and $\boldsymbol{p}$ simultaneously with logistic loss, we identify conditions under which the regularization paths directionally converge to their respective hard-margin SVM solutions where $\boldsymbol{v}$ separates the input features based on their labels. Interestingly, the SVM formulation of $\boldsymbol{p}$ is influenced by the support vector geometry of $\boldsymbol{v}$. Finally, we verify our theoretical findings via numerical experiments and provide insights.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge