Natural Policy Gradient for Average Reward Non-Stationary RL

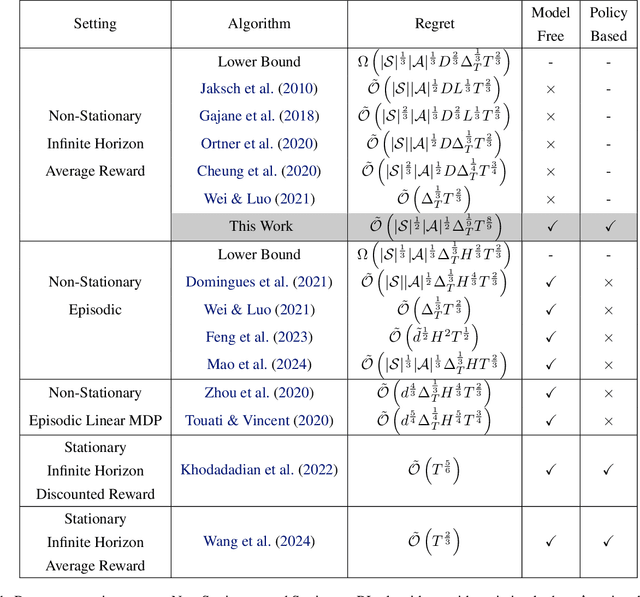
We consider the problem of non-stationary reinforcement learning (RL) in the infinite-horizon average-reward setting. We model it by a Markov Decision Process with time-varying rewards and transition probabilities, with a variation budget of $\Delta_T$. Existing non-stationary RL algorithms focus on model-based and model-free value-based methods. Policy-based methods despite their flexibility in practice are not theoretically well understood in non-stationary RL. We propose and analyze the first model-free policy-based algorithm, Non-Stationary Natural Actor-Critic (NS-NAC), a policy gradient method with a restart based exploration for change and a novel interpretation of learning rates as adapting factors. Further, we present a bandit-over-RL based parameter-free algorithm BORL-NS-NAC that does not require prior knowledge of the variation budget $\Delta_T$. We present a dynamic regret of $\tilde{\mathscr O}(|S|^{1/2}|A|^{1/2}\Delta_T^{1/6}T^{5/6})$ for both algorithms, where $T$ is the time horizon, and $|S|$, $|A|$ are the sizes of the state and action spaces. The regret analysis leverages a novel adaptation of the Lyapunov function analysis of NAC to dynamic environments and characterizes the effects of simultaneous updates in policy, value function estimate and changes in the environment.

Initialization Matters: Unraveling the Impact of Pre-Training on Federated Learning

Initializing with pre-trained models when learning on downstream tasks is becoming standard practice in machine learning. Several recent works explore the benefits of pre-trained initialization in a federated learning (FL) setting, where the downstream training is performed at the edge clients with heterogeneous data distribution. These works show that starting from a pre-trained model can substantially reduce the adverse impact of data heterogeneity on the test performance of a model trained in a federated setting, with no changes to the standard FedAvg training algorithm. In this work, we provide a deeper theoretical understanding of this phenomenon. To do so, we study the class of two-layer convolutional neural networks (CNNs) and provide bounds on the training error convergence and test error of such a network trained with FedAvg. We introduce the notion of aligned and misaligned filters at initialization and show that the data heterogeneity only affects learning on misaligned filters. Starting with a pre-trained model typically results in fewer misaligned filters at initialization, thus producing a lower test error even when the model is trained in a federated setting with data heterogeneity. Experiments in synthetic settings and practical FL training on CNNs verify our theoretical findings.

The Cost of Shuffling in Private Gradient Based Optimization

We consider the problem of differentially private (DP) convex empirical risk minimization (ERM). While the standard DP-SGD algorithm is theoretically well-established, practical implementations often rely on shuffled gradient methods that traverse the training data sequentially rather than sampling with replacement in each iteration. Despite their widespread use, the theoretical privacy-accuracy trade-offs of private shuffled gradient methods (\textit{DP-ShuffleG}) remain poorly understood, leading to a gap between theory and practice. In this work, we leverage privacy amplification by iteration (PABI) and a novel application of Stein's lemma to provide the first empirical excess risk bound of \textit{DP-ShuffleG}. Our result shows that data shuffling results in worse empirical excess risk for \textit{DP-ShuffleG} compared to DP-SGD. To address this limitation, we propose \textit{Interleaved-ShuffleG}, a hybrid approach that integrates public data samples in private optimization. By alternating optimization steps that use private and public samples, \textit{Interleaved-ShuffleG} effectively reduces empirical excess risk. Our analysis introduces a new optimization framework with surrogate objectives, adaptive noise injection, and a dissimilarity metric, which can be of independent interest. Our experiments on diverse datasets and tasks demonstrate the superiority of \textit{Interleaved-ShuffleG} over several baselines.

Federated Communication-Efficient Multi-Objective Optimization

We study a federated version of multi-objective optimization (MOO), where a single model is trained to optimize multiple objective functions. MOO has been extensively studied in the centralized setting but is less explored in federated or distributed settings. We propose FedCMOO, a novel communication-efficient federated multi-objective optimization (FMOO) algorithm that improves the error convergence performance of the model compared to existing approaches. Unlike prior works, the communication cost of FedCMOO does not scale with the number of objectives, as each client sends a single aggregated gradient, obtained using randomized SVD (singular value decomposition), to the central server. We provide a convergence analysis of the proposed method for smooth non-convex objective functions under milder assumptions than in prior work. In addition, we introduce a variant of FedCMOO that allows users to specify a preference over the objectives in terms of a desired ratio of the final objective values. Through extensive experiments, we demonstrate the superiority of our proposed method over baseline approaches.

Nonlinear Stochastic Gradient Descent and Heavy-tailed Noise: A Unified Framework and High-probability Guarantees

We study high-probability convergence in online learning, in the presence of heavy-tailed noise. To combat the heavy tails, a general framework of nonlinear SGD methods is considered, subsuming several popular nonlinearities like sign, quantization, component-wise and joint clipping. In our work the nonlinearity is treated in a black-box manner, allowing us to establish unified guarantees for a broad range of nonlinear methods. For symmetric noise and non-convex costs we establish convergence of gradient norm-squared, at a rate $\widetilde{\mathcal{O}}(t^{-1/4})$, while for the last iterate of strongly convex costs we establish convergence to the population optima, at a rate $\mathcal{O}(t^{-\zeta})$, where $\zeta \in (0,1)$ depends on noise and problem parameters. Further, if the noise is a (biased) mixture of symmetric and non-symmetric components, we show convergence to a neighbourhood of stationarity, whose size depends on the mixture coefficient, nonlinearity and noise. Compared to state-of-the-art, who only consider clipping and require unbiased noise with bounded $p$-th moments, $p \in (1,2]$, we provide guarantees for a broad class of nonlinearities, without any assumptions on noise moments. While the rate exponents in state-of-the-art depend on noise moments and vanish as $p \rightarrow 1$, our exponents are constant and strictly better whenever $p < 6/5$ for non-convex and $p < 8/7$ for strongly convex costs. Experiments validate our theory, demonstrating noise symmetry in real-life settings and showing that clipping is not always the optimal nonlinearity, further underlining the value of a general framework.

Debiasing Federated Learning with Correlated Client Participation

In cross-device federated learning (FL) with millions of mobile clients, only a small subset of clients participate in training in every communication round, and Federated Averaging (FedAvg) is the most popular algorithm in practice. Existing analyses of FedAvg usually assume the participating clients are independently sampled in each round from a uniform distribution, which does not reflect real-world scenarios. This paper introduces a theoretical framework that models client participation in FL as a Markov chain to study optimization convergence when clients have non-uniform and correlated participation across rounds. We apply this framework to analyze a more general and practical pattern: every client must wait a minimum number of $R$ rounds (minimum separation) before re-participating. We theoretically prove and empirically observe that increasing minimum separation reduces the bias induced by intrinsic non-uniformity of client availability in cross-device FL systems. Furthermore, we develop an effective debiasing algorithm for FedAvg that provably converges to the unbiased optimal solution under arbitrary minimum separation and unknown client availability distribution.

FedAST: Federated Asynchronous Simultaneous Training

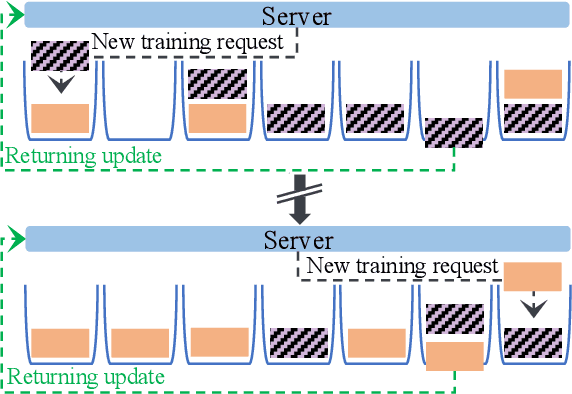
Federated Learning (FL) enables edge devices or clients to collaboratively train machine learning (ML) models without sharing their private data. Much of the existing work in FL focuses on efficiently learning a model for a single task. In this paper, we study simultaneous training of multiple FL models using a common set of clients. The few existing simultaneous training methods employ synchronous aggregation of client updates, which can cause significant delays because large models and/or slow clients can bottleneck the aggregation. On the other hand, a naive asynchronous aggregation is adversely affected by stale client updates. We propose FedAST, a buffered asynchronous federated simultaneous training algorithm that overcomes bottlenecks from slow models and adaptively allocates client resources across heterogeneous tasks. We provide theoretical convergence guarantees for FedAST for smooth non-convex objective functions. Extensive experiments over multiple real-world datasets demonstrate that our proposed method outperforms existing simultaneous FL approaches, achieving up to 46.0% reduction in time to train multiple tasks to completion.

Correlation Aware Sparsified Mean Estimation Using Random Projection

We study the problem of communication-efficient distributed vector mean estimation, a commonly used subroutine in distributed optimization and Federated Learning (FL). Rand-$k$ sparsification is a commonly used technique to reduce communication cost, where each client sends $k < d$ of its coordinates to the server. However, Rand-$k$ is agnostic to any correlations, that might exist between clients in practical scenarios. The recently proposed Rand-$k$-Spatial estimator leverages the cross-client correlation information at the server to improve Rand-$k$'s performance. Yet, the performance of Rand-$k$-Spatial is suboptimal. We propose the Rand-Proj-Spatial estimator with a more flexible encoding-decoding procedure, which generalizes the encoding of Rand-$k$ by projecting the client vectors to a random $k$-dimensional subspace. We utilize Subsampled Randomized Hadamard Transform (SRHT) as the projection matrix and show that Rand-Proj-Spatial with SRHT outperforms Rand-$k$-Spatial, using the correlation information more efficiently. Furthermore, we propose an approach to incorporate varying degrees of correlation and suggest a practical variant of Rand-Proj-Spatial when the correlation information is not available to the server. Experiments on real-world distributed optimization tasks showcase the superior performance of Rand-Proj-Spatial compared to Rand-$k$-Spatial and other more sophisticated sparsification techniques.

High-probability Convergence Bounds for Nonlinear Stochastic Gradient Descent Under Heavy-tailed Noise

Several recent works have studied the convergence \textit{in high probability} of stochastic gradient descent (SGD) and its clipped variant. Compared to vanilla SGD, clipped SGD is practically more stable and has the additional theoretical benefit of logarithmic dependence on the failure probability. However, the convergence of other practical nonlinear variants of SGD, e.g., sign SGD, quantized SGD and normalized SGD, that achieve improved communication efficiency or accelerated convergence is much less understood. In this work, we study the convergence bounds \textit{in high probability} of a broad class of nonlinear SGD methods. For strongly convex loss functions with Lipschitz continuous gradients, we prove a logarithmic dependence on the failure probability, even when the noise is heavy-tailed. Strictly more general than the results for clipped SGD, our results hold for any nonlinearity with bounded (component-wise or joint) outputs, such as clipping, normalization, and quantization. Further, existing results with heavy-tailed noise assume bounded $\eta$-th central moments, with $\eta \in (1,2]$. In contrast, our refined analysis works even for $\eta=1$, strictly relaxing the noise moment assumptions in the literature.

Federated Multi-Sequence Stochastic Approximation with Local Hypergradient Estimation

Stochastic approximation with multiple coupled sequences (MSA) has found broad applications in machine learning as it encompasses a rich class of problems including bilevel optimization (BLO), multi-level compositional optimization (MCO), and reinforcement learning (specifically, actor-critic methods). However, designing provably-efficient federated algorithms for MSA has been an elusive question even for the special case of double sequence approximation (DSA). Towards this goal, we develop FedMSA which is the first federated algorithm for MSA, and establish its near-optimal communication complexity. As core novelties, (i) FedMSA enables the provable estimation of hypergradients in BLO and MCO via local client updates, which has been a notable bottleneck in prior theory, and (ii) our convergence guarantees are sensitive to the heterogeneity-level of the problem. We also incorporate momentum and variance reduction techniques to achieve further acceleration leading to near-optimal rates. Finally, we provide experiments that support our theory and demonstrate the empirical benefits of FedMSA. As an example, FedMSA enables order-of-magnitude savings in communication rounds compared to prior federated BLO schemes.