Large Deviations and Improved Mean-squared Error Rates of Nonlinear SGD: Heavy-tailed Noise and Power of Symmetry

We study large deviations and mean-squared error (MSE) guarantees of a general framework of nonlinear stochastic gradient methods in the online setting, in the presence of heavy-tailed noise. Unlike existing works that rely on the closed form of a nonlinearity (typically clipping), our framework treats the nonlinearity in a black-box manner, allowing us to provide unified guarantees for a broad class of bounded nonlinearities, including many popular ones, like sign, quantization, normalization, as well as component-wise and joint clipping. We provide several strong results for a broad range of step-sizes in the presence of heavy-tailed noise with symmetric probability density function, positive in a neighbourhood of zero and potentially unbounded moments. In particular, for non-convex costs we provide a large deviation upper bound for the minimum norm-squared of gradients, showing an asymptotic tail decay on an exponential scale, at a rate $\sqrt{t} / \log(t)$. We establish the accompanying rate function, showing an explicit dependence on the choice of step-size, nonlinearity, noise and problem parameters. Next, for non-convex costs and the minimum norm-squared of gradients, we derive the optimal MSE rate $\widetilde{\mathcal{O}}(t^{-1/2})$. Moreover, for strongly convex costs and the last iterate, we provide an MSE rate that can be made arbitrarily close to the optimal rate $\mathcal{O}(t^{-1})$, improving on the state-of-the-art results in the presence of heavy-tailed noise. Finally, we establish almost sure convergence of the minimum norm-squared of gradients, providing an explicit rate, which can be made arbitrarily close to $o(t^{-1/4})$.

Nonlinear Stochastic Gradient Descent and Heavy-tailed Noise: A Unified Framework and High-probability Guarantees

We study high-probability convergence in online learning, in the presence of heavy-tailed noise. To combat the heavy tails, a general framework of nonlinear SGD methods is considered, subsuming several popular nonlinearities like sign, quantization, component-wise and joint clipping. In our work the nonlinearity is treated in a black-box manner, allowing us to establish unified guarantees for a broad range of nonlinear methods. For symmetric noise and non-convex costs we establish convergence of gradient norm-squared, at a rate $\widetilde{\mathcal{O}}(t^{-1/4})$, while for the last iterate of strongly convex costs we establish convergence to the population optima, at a rate $\mathcal{O}(t^{-\zeta})$, where $\zeta \in (0,1)$ depends on noise and problem parameters. Further, if the noise is a (biased) mixture of symmetric and non-symmetric components, we show convergence to a neighbourhood of stationarity, whose size depends on the mixture coefficient, nonlinearity and noise. Compared to state-of-the-art, who only consider clipping and require unbiased noise with bounded $p$-th moments, $p \in (1,2]$, we provide guarantees for a broad class of nonlinearities, without any assumptions on noise moments. While the rate exponents in state-of-the-art depend on noise moments and vanish as $p \rightarrow 1$, our exponents are constant and strictly better whenever $p < 6/5$ for non-convex and $p < 8/7$ for strongly convex costs. Experiments validate our theory, demonstrating noise symmetry in real-life settings and showing that clipping is not always the optimal nonlinearity, further underlining the value of a general framework.

High-probability Convergence Bounds for Nonlinear Stochastic Gradient Descent Under Heavy-tailed Noise

Several recent works have studied the convergence \textit{in high probability} of stochastic gradient descent (SGD) and its clipped variant. Compared to vanilla SGD, clipped SGD is practically more stable and has the additional theoretical benefit of logarithmic dependence on the failure probability. However, the convergence of other practical nonlinear variants of SGD, e.g., sign SGD, quantized SGD and normalized SGD, that achieve improved communication efficiency or accelerated convergence is much less understood. In this work, we study the convergence bounds \textit{in high probability} of a broad class of nonlinear SGD methods. For strongly convex loss functions with Lipschitz continuous gradients, we prove a logarithmic dependence on the failure probability, even when the noise is heavy-tailed. Strictly more general than the results for clipped SGD, our results hold for any nonlinearity with bounded (component-wise or joint) outputs, such as clipping, normalization, and quantization. Further, existing results with heavy-tailed noise assume bounded $\eta$-th central moments, with $\eta \in (1,2]$. In contrast, our refined analysis works even for $\eta=1$, strictly relaxing the noise moment assumptions in the literature.

Large deviations rates for stochastic gradient descent with strongly convex functions

Recent works have shown that high probability metrics with stochastic gradient descent (SGD) exhibit informativeness and in some cases advantage over the commonly adopted mean-square error-based ones. In this work we provide a formal framework for the study of general high probability bounds with SGD, based on the theory of large deviations. The framework allows for a generic (not-necessarily bounded) gradient noise satisfying mild technical assumptions, allowing for the dependence of the noise distribution on the current iterate. Under the preceding assumptions, we find an upper large deviations bound for SGD with strongly convex functions. The corresponding rate function captures analytical dependence on the noise distribution and other problem parameters. This is in contrast with conventional mean-square error analysis that captures only the noise dependence through the variance and does not capture the effect of higher order moments nor interplay between the noise geometry and the shape of the cost function. We also derive exact large deviation rates for the case when the objective function is quadratic and show that the obtained function matches the one from the general upper bound hence showing the tightness of the general upper bound. Numerical examples illustrate and corroborate theoretical findings.

One-Shot Federated Learning for Model Clustering and Learning in Heterogeneous Environments

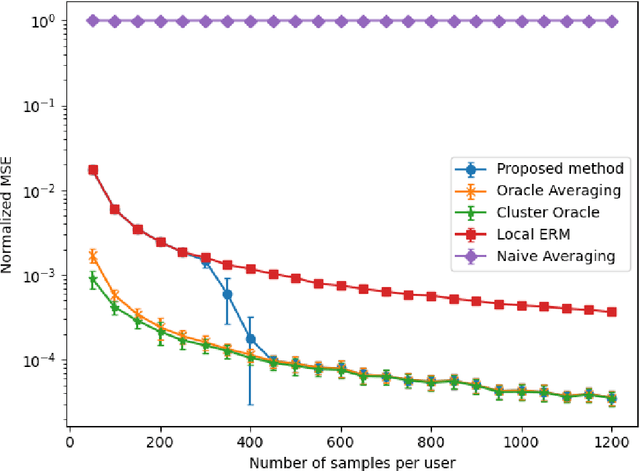
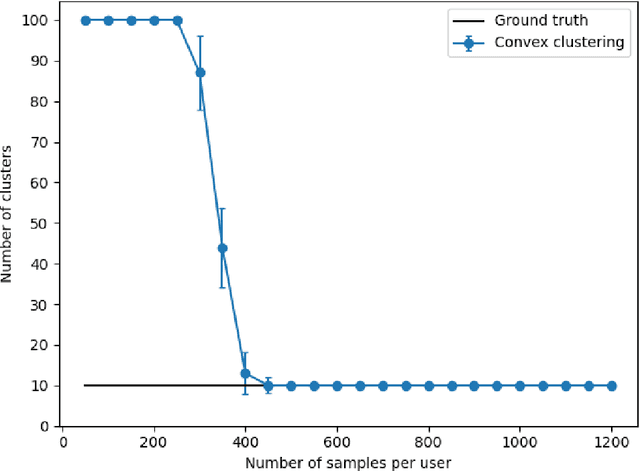
We propose a communication efficient approach for federated learning in heterogeneous environments. The system heterogeneity is reflected in the presence of $K$ different data distributions, with each user sampling data from only one of $K$ distributions. The proposed approach requires only one communication round between the users and server, thus significantly reducing the communication cost. Moreover, the proposed method provides strong learning guarantees in heterogeneous environments, by achieving the optimal mean-squared error (MSE) rates in terms of the sample size, i.e., matching the MSE guarantees achieved by learning on all data points belonging to users with the same data distribution, provided that the number of data points per user is above a threshold that we explicitly characterize in terms of system parameters. Remarkably, this is achieved without requiring any knowledge of the underlying distributions, or even the true number of distributions $K$. Numerical experiments illustrate our findings and underline the performance of the proposed method.

Nonlinear gradient mappings and stochastic optimization: A general framework with applications to heavy-tail noise

We introduce a general framework for nonlinear stochastic gradient descent (SGD) for the scenarios when gradient noise exhibits heavy tails. The proposed framework subsumes several popular nonlinearity choices, like clipped, normalized, signed or quantized gradient, but we also consider novel nonlinearity choices. We establish for the considered class of methods strong convergence guarantees assuming a strongly convex cost function with Lipschitz continuous gradients under very general assumptions on the gradient noise. Most notably, we show that, for a nonlinearity with bounded outputs and for the gradient noise that may not have finite moments of order greater than one, the nonlinear SGD's mean squared error (MSE), or equivalently, the expected cost function's optimality gap, converges to zero at rate~$O(1/t^\zeta)$, $\zeta \in (0,1)$. In contrast, for the same noise setting, the linear SGD generates a sequence with unbounded variances. Furthermore, for the nonlinearities that can be decoupled component wise, like, e.g., sign gradient or component-wise clipping, we show that the nonlinear SGD asymptotically (locally) achieves a $O(1/t)$ rate in the weak convergence sense and explicitly quantify the corresponding asymptotic variance. Experiments show that, while our framework is more general than existing studies of SGD under heavy-tail noise, several easy-to-implement nonlinearities from our framework are competitive with state of the art alternatives on real data sets with heavy tail noises.

Gradient Based Clustering

We propose a general approach for distance based clustering, using the gradient of the cost function that measures clustering quality with respect to cluster assignments and cluster center positions. The approach is an iterative two step procedure (alternating between cluster assignment and cluster center updates) and is applicable to a wide range of functions, satisfying some mild assumptions. The main advantage of the proposed approach is a simple and computationally cheap update rule. Unlike previous methods that specialize to a specific formulation of the clustering problem, our approach is applicable to a wide range of costs, including non-Bregman clustering methods based on the Huber loss. We analyze the convergence of the proposed algorithm, and show that it converges to the set of appropriately defined fixed points, under arbitrary center initialization. In the special case of Bregman cost functions, the algorithm converges to the set of centroidal Voronoi partitions, which is consistent with prior works. Numerical experiments on real data demonstrate the effectiveness of the proposed method.

Personalized Federated Learning via Convex Clustering

We propose a parametric family of algorithms for personalized federated learning with locally convex user costs. The proposed framework is based on a generalization of convex clustering in which the differences between different users' models are penalized via a sum-of-norms penalty, weighted by a penalty parameter $\lambda$. The proposed approach enables "automatic" model clustering, without prior knowledge of the hidden cluster structure, nor the number of clusters. Analytical bounds on the weight parameter, that lead to simultaneous personalization, generalization and automatic model clustering are provided. The solution to the formulated problem enables personalization, by providing different models across different clusters, and generalization, by providing models different than the per-user models computed in isolation. We then provide an efficient algorithm based on the Parallel Direction Method of Multipliers (PDMM) to solve the proposed formulation in a federated server-users setting. Numerical experiments corroborate our findings. As an interesting byproduct, our results provide several generalizations to convex clustering.