Ravan: Multi-Head Low-Rank Adaptation for Federated Fine-Tuning

Large language models (LLMs) have not yet effectively leveraged the vast amounts of edge-device data, and federated learning (FL) offers a promising paradigm to collaboratively fine-tune LLMs without transferring private edge data to the cloud. To operate within the computation and communication constraints of edge devices, recent literature on federated fine-tuning of LLMs proposes the use of low-rank adaptation (LoRA) and similar parameter-efficient methods. However, LoRA-based methods suffer from accuracy degradation in FL settings, primarily because of data and computational heterogeneity across clients. We propose \textsc{Ravan}, an adaptive multi-head LoRA method that balances parameter efficiency and model expressivity by reparameterizing the weight updates as the sum of multiple LoRA heads $s_i\textbf{B}_i\textbf{H}_i\textbf{A}_i$ in which only the core matrices $\textbf{H}_i$ and their lightweight scaling factors $s_i$ are trained. These trainable scaling factors let the optimization focus on the most useful heads, recovering a higher-rank approximation of the full update without increasing the number of communicated parameters since clients upload $s_i\textbf{H}_i$ directly. Experiments on vision and language benchmarks show that \textsc{Ravan} improves test accuracy by 2-8\% over prior parameter-efficient baselines, making it a robust and scalable solution for federated fine-tuning of LLMs.

Navigating the Accuracy-Size Trade-Off with Flexible Model Merging

Model merging has emerged as an efficient method to combine multiple single-task fine-tuned models. The merged model can enjoy multi-task capabilities without expensive training. While promising, merging into a single model often suffers from an accuracy gap with respect to individual fine-tuned models. On the other hand, deploying all individual fine-tuned models incurs high costs. We propose FlexMerge, a novel data-free model merging framework to flexibly generate merged models of varying sizes, spanning the spectrum from a single merged model to retaining all individual fine-tuned models. FlexMerge treats fine-tuned models as collections of sequential blocks and progressively merges them using any existing data-free merging method, halting at a desired size. We systematically explore the accuracy-size trade-off exhibited by different merging algorithms in combination with FlexMerge. Extensive experiments on vision and NLP benchmarks, with up to 30 tasks, reveal that even modestly larger merged models can provide substantial accuracy improvements over a single model. By offering fine-grained control over fused model size, FlexMerge provides a flexible, data-free, and high-performance solution for diverse deployment scenarios.

Natural Policy Gradient for Average Reward Non-Stationary RL

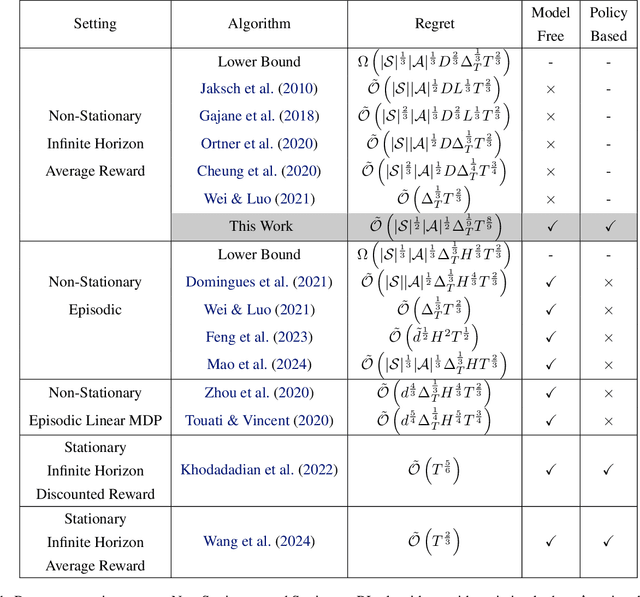
We consider the problem of non-stationary reinforcement learning (RL) in the infinite-horizon average-reward setting. We model it by a Markov Decision Process with time-varying rewards and transition probabilities, with a variation budget of $\Delta_T$. Existing non-stationary RL algorithms focus on model-based and model-free value-based methods. Policy-based methods despite their flexibility in practice are not theoretically well understood in non-stationary RL. We propose and analyze the first model-free policy-based algorithm, Non-Stationary Natural Actor-Critic (NS-NAC), a policy gradient method with a restart based exploration for change and a novel interpretation of learning rates as adapting factors. Further, we present a bandit-over-RL based parameter-free algorithm BORL-NS-NAC that does not require prior knowledge of the variation budget $\Delta_T$. We present a dynamic regret of $\tilde{\mathscr O}(|S|^{1/2}|A|^{1/2}\Delta_T^{1/6}T^{5/6})$ for both algorithms, where $T$ is the time horizon, and $|S|$, $|A|$ are the sizes of the state and action spaces. The regret analysis leverages a novel adaptation of the Lyapunov function analysis of NAC to dynamic environments and characterizes the effects of simultaneous updates in policy, value function estimate and changes in the environment.

Initialization Matters: Unraveling the Impact of Pre-Training on Federated Learning

Initializing with pre-trained models when learning on downstream tasks is becoming standard practice in machine learning. Several recent works explore the benefits of pre-trained initialization in a federated learning (FL) setting, where the downstream training is performed at the edge clients with heterogeneous data distribution. These works show that starting from a pre-trained model can substantially reduce the adverse impact of data heterogeneity on the test performance of a model trained in a federated setting, with no changes to the standard FedAvg training algorithm. In this work, we provide a deeper theoretical understanding of this phenomenon. To do so, we study the class of two-layer convolutional neural networks (CNNs) and provide bounds on the training error convergence and test error of such a network trained with FedAvg. We introduce the notion of aligned and misaligned filters at initialization and show that the data heterogeneity only affects learning on misaligned filters. Starting with a pre-trained model typically results in fewer misaligned filters at initialization, thus producing a lower test error even when the model is trained in a federated setting with data heterogeneity. Experiments in synthetic settings and practical FL training on CNNs verify our theoretical findings.

The Cost of Shuffling in Private Gradient Based Optimization

We consider the problem of differentially private (DP) convex empirical risk minimization (ERM). While the standard DP-SGD algorithm is theoretically well-established, practical implementations often rely on shuffled gradient methods that traverse the training data sequentially rather than sampling with replacement in each iteration. Despite their widespread use, the theoretical privacy-accuracy trade-offs of private shuffled gradient methods (\textit{DP-ShuffleG}) remain poorly understood, leading to a gap between theory and practice. In this work, we leverage privacy amplification by iteration (PABI) and a novel application of Stein's lemma to provide the first empirical excess risk bound of \textit{DP-ShuffleG}. Our result shows that data shuffling results in worse empirical excess risk for \textit{DP-ShuffleG} compared to DP-SGD. To address this limitation, we propose \textit{Interleaved-ShuffleG}, a hybrid approach that integrates public data samples in private optimization. By alternating optimization steps that use private and public samples, \textit{Interleaved-ShuffleG} effectively reduces empirical excess risk. Our analysis introduces a new optimization framework with surrogate objectives, adaptive noise injection, and a dissimilarity metric, which can be of independent interest. Our experiments on diverse datasets and tasks demonstrate the superiority of \textit{Interleaved-ShuffleG} over several baselines.

Optimized Tradeoffs for Private Prediction with Majority Ensembling

We study a classical problem in private prediction, the problem of computing an $(m\epsilon, \delta)$-differentially private majority of $K$ $(\epsilon, \Delta)$-differentially private algorithms for $1 \leq m \leq K$ and $1 > \delta \geq \Delta \geq 0$. Standard methods such as subsampling or randomized response are widely used, but do they provide optimal privacy-utility tradeoffs? To answer this, we introduce the Data-dependent Randomized Response Majority (DaRRM) algorithm. It is parameterized by a data-dependent noise function $\gamma$, and enables efficient utility optimization over the class of all private algorithms, encompassing those standard methods. We show that maximizing the utility of an $(m\epsilon, \delta)$-private majority algorithm can be computed tractably through an optimization problem for any $m \leq K$ by a novel structural result that reduces the infinitely many privacy constraints into a polynomial set. In some settings, we show that DaRRM provably enjoys a privacy gain of a factor of 2 over common baselines, with fixed utility. Lastly, we demonstrate the strong empirical effectiveness of our first-of-its-kind privacy-constrained utility optimization for ensembling labels for private prediction from private teachers in image classification. Notably, our DaRRM framework with an optimized $\gamma$ exhibits substantial utility gains when compared against several baselines.

Federated Communication-Efficient Multi-Objective Optimization

We study a federated version of multi-objective optimization (MOO), where a single model is trained to optimize multiple objective functions. MOO has been extensively studied in the centralized setting but is less explored in federated or distributed settings. We propose FedCMOO, a novel communication-efficient federated multi-objective optimization (FMOO) algorithm that improves the error convergence performance of the model compared to existing approaches. Unlike prior works, the communication cost of FedCMOO does not scale with the number of objectives, as each client sends a single aggregated gradient, obtained using randomized SVD (singular value decomposition), to the central server. We provide a convergence analysis of the proposed method for smooth non-convex objective functions under milder assumptions than in prior work. In addition, we introduce a variant of FedCMOO that allows users to specify a preference over the objectives in terms of a desired ratio of the final objective values. Through extensive experiments, we demonstrate the superiority of our proposed method over baseline approaches.

Nonlinear Stochastic Gradient Descent and Heavy-tailed Noise: A Unified Framework and High-probability Guarantees

We study high-probability convergence in online learning, in the presence of heavy-tailed noise. To combat the heavy tails, a general framework of nonlinear SGD methods is considered, subsuming several popular nonlinearities like sign, quantization, component-wise and joint clipping. In our work the nonlinearity is treated in a black-box manner, allowing us to establish unified guarantees for a broad range of nonlinear methods. For symmetric noise and non-convex costs we establish convergence of gradient norm-squared, at a rate $\widetilde{\mathcal{O}}(t^{-1/4})$, while for the last iterate of strongly convex costs we establish convergence to the population optima, at a rate $\mathcal{O}(t^{-\zeta})$, where $\zeta \in (0,1)$ depends on noise and problem parameters. Further, if the noise is a (biased) mixture of symmetric and non-symmetric components, we show convergence to a neighbourhood of stationarity, whose size depends on the mixture coefficient, nonlinearity and noise. Compared to state-of-the-art, who only consider clipping and require unbiased noise with bounded $p$-th moments, $p \in (1,2]$, we provide guarantees for a broad class of nonlinearities, without any assumptions on noise moments. While the rate exponents in state-of-the-art depend on noise moments and vanish as $p \rightarrow 1$, our exponents are constant and strictly better whenever $p < 6/5$ for non-convex and $p < 8/7$ for strongly convex costs. Experiments validate our theory, demonstrating noise symmetry in real-life settings and showing that clipping is not always the optimal nonlinearity, further underlining the value of a general framework.

FedECADO: A Dynamical System Model of Federated Learning

Federated learning harnesses the power of distributed optimization to train a unified machine learning model across separate clients. However, heterogeneous data distributions and computational workloads can lead to inconsistent updates and limit model performance. This work tackles these challenges by proposing FedECADO, a new algorithm inspired by a dynamical system representation of the federated learning process. FedECADO addresses non-IID data distribution through an aggregate sensitivity model that reflects the amount of data processed by each client. To tackle heterogeneous computing, we design a multi-rate integration method with adaptive step-size selections that synchronizes active client updates in continuous time. Compared to prominent techniques, including FedProx and FedNova, FedECADO achieves higher classification accuracies in numerous heterogeneous scenarios.

Debiasing Federated Learning with Correlated Client Participation

In cross-device federated learning (FL) with millions of mobile clients, only a small subset of clients participate in training in every communication round, and Federated Averaging (FedAvg) is the most popular algorithm in practice. Existing analyses of FedAvg usually assume the participating clients are independently sampled in each round from a uniform distribution, which does not reflect real-world scenarios. This paper introduces a theoretical framework that models client participation in FL as a Markov chain to study optimization convergence when clients have non-uniform and correlated participation across rounds. We apply this framework to analyze a more general and practical pattern: every client must wait a minimum number of $R$ rounds (minimum separation) before re-participating. We theoretically prove and empirically observe that increasing minimum separation reduces the bias induced by intrinsic non-uniformity of client availability in cross-device FL systems. Furthermore, we develop an effective debiasing algorithm for FedAvg that provably converges to the unbiased optimal solution under arbitrary minimum separation and unknown client availability distribution.