Optimized Tradeoffs for Private Prediction with Majority Ensembling

We study a classical problem in private prediction, the problem of computing an $(m\epsilon, \delta)$-differentially private majority of $K$ $(\epsilon, \Delta)$-differentially private algorithms for $1 \leq m \leq K$ and $1 > \delta \geq \Delta \geq 0$. Standard methods such as subsampling or randomized response are widely used, but do they provide optimal privacy-utility tradeoffs? To answer this, we introduce the Data-dependent Randomized Response Majority (DaRRM) algorithm. It is parameterized by a data-dependent noise function $\gamma$, and enables efficient utility optimization over the class of all private algorithms, encompassing those standard methods. We show that maximizing the utility of an $(m\epsilon, \delta)$-private majority algorithm can be computed tractably through an optimization problem for any $m \leq K$ by a novel structural result that reduces the infinitely many privacy constraints into a polynomial set. In some settings, we show that DaRRM provably enjoys a privacy gain of a factor of 2 over common baselines, with fixed utility. Lastly, we demonstrate the strong empirical effectiveness of our first-of-its-kind privacy-constrained utility optimization for ensembling labels for private prediction from private teachers in image classification. Notably, our DaRRM framework with an optimized $\gamma$ exhibits substantial utility gains when compared against several baselines.

Ontology of Belief Diversity: A Community-Based Epistemological Approach

AI applications across classification, fairness, and human interaction often implicitly require ontologies of social concepts. Constructing these well, especially when there are many relevant categories, is a controversial task but is crucial for achieving meaningful inclusivity. Here, we focus on developing a pragmatic ontology of belief systems, which is a complex and often controversial space. By iterating on our community-based design until mutual agreement is reached, we found that epistemological methods were best for categorizing the fundamental ways beliefs differ, maximally respecting our principles of inclusivity and brevity. We demonstrate our methodology's utility and interpretability via user studies in term annotation and sentiment analysis experiments for belief fairness in language models.

Hardness of Low Rank Approximation of Entrywise Transformed Matrix Products

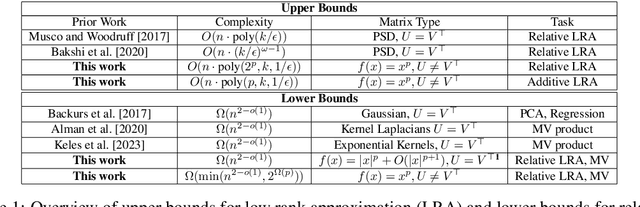
Inspired by fast algorithms in natural language processing, we study low rank approximation in the entrywise transformed setting where we want to find a good rank $k$ approximation to $f(U \cdot V)$, where $U, V^\top \in \mathbb{R}^{n \times r}$ are given, $r = O(\log(n))$, and $f(x)$ is a general scalar function. Previous work in sublinear low rank approximation has shown that if both (1) $U = V^\top$ and (2) $f(x)$ is a PSD kernel function, then there is an $O(nk^{\omega-1})$ time constant relative error approximation algorithm, where $\omega \approx 2.376$ is the exponent of matrix multiplication. We give the first conditional time hardness results for this problem, demonstrating that both conditions (1) and (2) are in fact necessary for getting better than $n^{2-o(1)}$ time for a relative error low rank approximation for a wide class of functions. We give novel reductions from the Strong Exponential Time Hypothesis (SETH) that rely on lower bounding the leverage scores of flat sparse vectors and hold even when the rank of the transformed matrix $f(UV)$ and the target rank are $n^{o(1)}$, and when $U = V^\top$. Furthermore, even when $f(x) = x^p$ is a simple polynomial, we give runtime lower bounds in the case when $U \neq V^\top$ of the form $\Omega(\min(n^{2-o(1)}, \Omega(2^p)))$. Lastly, we demonstrate that our lower bounds are tight by giving an $O(n \cdot \text{poly}(k, 2^p, 1/\epsilon))$ time relative error approximation algorithm and a fast $O(n \cdot \text{poly}(k, p, 1/\epsilon))$ additive error approximation using fast tensor-based sketching. Additionally, since our low rank algorithms rely on matrix-vector product subroutines, our lower bounds extend to show that computing $f(UV)W$, for even a small matrix $W$, requires $\Omega(n^{2-o(1)})$ time.

Leveraging Contextual Counterfactuals Toward Belief Calibration

Beliefs and values are increasingly being incorporated into our AI systems through alignment processes, such as carefully curating data collection principles or regularizing the loss function used for training. However, the meta-alignment problem is that these human beliefs are diverse and not aligned across populations; furthermore, the implicit strength of each belief may not be well calibrated even among humans, especially when trying to generalize across contexts. Specifically, in high regret situations, we observe that contextual counterfactuals and recourse costs are particularly important in updating a decision maker's beliefs and the strengths to which such beliefs are held. Therefore, we argue that including counterfactuals is key to an accurate calibration of beliefs during alignment. To do this, we first segment belief diversity into two categories: subjectivity (across individuals within a population) and epistemic uncertainty (within an individual across different contexts). By leveraging our notion of epistemic uncertainty, we introduce `the belief calibration cycle' framework to more holistically calibrate this diversity of beliefs with context-driven counterfactual reasoning by using a multi-objective optimization. We empirically apply our framework for finding a Pareto frontier of clustered optimal belief strengths that generalize across different contexts, demonstrating its efficacy on a toy dataset for credit decisions.

Leveraging Initial Hints for Free in Stochastic Linear Bandits

We study the setting of optimizing with bandit feedback with additional prior knowledge provided to the learner in the form of an initial hint of the optimal action. We present a novel algorithm for stochastic linear bandits that uses this hint to improve its regret to $\tilde O(\sqrt{T})$ when the hint is accurate, while maintaining a minimax-optimal $\tilde O(d\sqrt{T})$ regret independent of the quality of the hint. Furthermore, we provide a Pareto frontier of tight tradeoffs between best-case and worst-case regret, with matching lower bounds. Perhaps surprisingly, our work shows that leveraging a hint shows provable gains without sacrificing worst-case performance, implying that our algorithm adapts to the quality of the hint for free. We also provide an extension of our algorithm to the case of $m$ initial hints, showing that we can achieve a $\tilde O(m^{2/3}\sqrt{T})$ regret.